张利萍，刘桂华，可杨

　　（西南科技大学 信息工程学院，四川 绵阳 621000）

       摘要：在基于相位轮廓术进行双目三维重建时，传统的双目测量系统在遮挡条件下无法获取双目相机公共视野以外的区域的点云数据，导致扫描结果出现测量空洞或者点云数量减少，从而不能通过立体视觉进行三维重建。对此，提出了一种基于双目点云重建单目点云的方法，系统无需增加其他操作过程，单次扫描就能同时获得双目点云和精度较高的左右单目点云。在对飞机模型的测量中，利用该方法填补了双目测量在机翼附近出现的数据丢失，提高了测量结果的完整性。

　　关键词：三维重建；遮挡；相位；点云

　　中图分类号：TP391文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.04.021

　　引用格式：张利萍，刘桂华，可杨.基于单双目融合的遮挡区域点云获取技术研究［J］.微型机与应用，2017,36（4）：70-73.

0引言

　　基于相位测量轮廓术的三维测量技术作为一种主动式非接触光学测量方法，因具有全场分析、测量精度高、非接触等优点，正逐渐成为当前三维测量领域内最重要和最热门的一个研究分支，在工业检测、质量控制、逆向工程、生物医学、虚拟现实、文物保护等众多领域中具有广泛的应用［14］。常用的基于相位轮廓术的三维重建系统按相机个数可以分为单目系统和双目系统，单目测量系统只需一个摄像机，通过相位值直接解算得到物体的高度信息，双目系统则将相位作为匹配的一个特征，利用立体视觉求取物体的三维特征。这两种结构都有各自的优点，但单目系统在测量精度以及抗噪性上与双目视觉系统有一定的差距。故双目视觉系统在实际中的应用更广泛。

　　双目视觉系统由于其三维坐标的获取是基于两相机对应像素点的匹配，在视场方面有一定的局限性，对于遮挡、阴影等情况，在重建过程中容易出现数据的缺失。遮挡是指匹配图像对时，一个图像的像素在另一个图像中找不到对应匹配点，导致最终出现匹配错误，不仅被遮挡的点难以得到正确的视差值，还会给遮挡区域附近点的匹配带来负面效果。如果靠多次扫描拼合或后期点云处理，则较复杂［5］。IKEMURA S等人在用TOF相机获得深度信息的基础上，提出了相关深度相似特征来进行遮挡判断，该设备成本昂贵，且只能应用在特殊场合中［6］。MA Y等人将深度和遮挡率相结合，但是当遮挡对象出现相似视差变化的情况，就很难解决遮挡问题［7］。Jin Xin等人将编码和遮挡区域的分割相结合对遮挡关系进行判断，减少了计算量，但是必须完全清楚场景中的对象时才可用此方法［8］。耿英楠提出基于RGB矢量空间的三目立体匹配方法，提高了遮挡区的匹配正确率，但是匹配过程比较复杂［9］。许雯提出了基于LRC遮挡检测的改进的ASW算法，对检测出的遮挡区域进行填充，提高了整体视差图的匹配质量［10］。以上算法对解决立体匹配中的遮挡问题都有很好的效果，但是由于匹配过程中算法复杂，计算量庞大或者成本较高等各种原因，导致在实际中的应用性不强。针对上述问题，结合单双目测量系统各自的优点，提出了一种基于双目点云重建单目点云的新方法，系统无需增加其他操作过程，单次扫描就能同时获得双目点云和精度较高的左右单目点云，很好地提升了测量数据的完整性。

1双目三维重建原理

　　基于相位轮廓术的物体三维轮廓测量原理是投影仪向被测物体投射一组光强呈正弦分布的光栅，左、右两个相机同步采集受物体表面调制后的光栅，然后根据采集的图像获取毎个像素的相位值，最后根据标定参数，应用三角测量原理获得物体表面三维数据。

　　双目立体视觉系统中三维空间点的成像模型如图1所示，设空间点A在左右相机Cl和Cr上的投影分别为al和ar，al和ar为一对匹配点，则可以唯一确定A点的空间位置，即直线Olal和直线Orar的交点。

　　设左摄像机位于世界坐标系O-xyz原点，图像坐标系为Ol－XlYl，有效焦距为fl，右摄像机坐标系为Or-xryrzr，有效焦距为fr，由摄像机透视投影模型以及两摄像机之间的位置关系，空间点A的三维坐标可以表示为：

　　式中Xi=(ui-u0i)*dx,Yi=(vi-v0i)*dy,i=l,r。其中(Xi,Yi)为像素物理坐标，(u,v)为像素图像坐标，(u0,v0)为像素坐标原点，dx、dy为像元尺寸。右相机和左相机间的旋转矩阵

　　由式（1）可知，通过双目摄像机标定求出左、右相机焦距fl、fr，旋转矩阵R和平移矩阵T，通过极线约束原理求出左右图像中匹配点对的图像坐标，就可以得到被测物的三维点云数据。

　　在利用双目视觉原理进行三维重建的过程中，常常由于相机拍摄视角或者物体表面轮廓较复杂等原因，导致物体表面某些场景点只能在双目视觉系统中的一个摄像机中可见，而在另一个摄像机中不可见，图像上这些点称为双目半遮挡点。它们通常存在于物体边缘和场景不连续等地方，而这些地方又是视觉中要处理的关键点。

2单目重建技术

　　现有的单双目点云重建方法一般采用两个相机分别与投影仪组成单目测量系统来补充双目测量结果的方式。在获取单目点云的方法上，本文采用盖绍彦提出的相位高度映射模型［11］，此模型对摄像机、投影装置以及标定平面的位置关系无严格要求，提高了系统的可操作性。本节基于该模型提出一种使用双目点云来优化模型参数，获得单目点云的方法，与单纯依靠双目的测量系统相比，使用此方法能够有效地改进系统的测量范围和提高测量结果的完整性。

　　2.1相位恢复高度模型

　　系统模型［11］如图2所示，参考坐标系Ωw(OXYZ)是基于投影设备建立的：OXY平面平行于投影面，光栅条纹平行于Y轴，投影中心OP经过Z轴。摄像机坐标系Ωc(OcXcYcZc)原点Oc位于镜头光心，Zc位于光轴，Xc、Yc分别平行于摄像机成像面的横轴、纵轴。o1mn表示摄像机成像面上的图像坐标系。

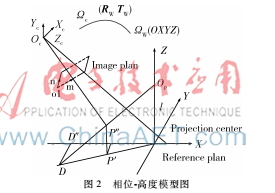
　　设物点P在参考坐标系ΩW中的坐标为(X,Y,Z)，在摄像机坐标系Ωc中的坐标为(Xc,Yc,Zc)，有

　　可以推导出P点的相位θ与其三维坐标(Xc,Yc,Zc)的关系如式（3）所示:

　　式（3）是θ-（Xc,Yc,Zc）映射模型的关系式，a1~a8为待标定的系统参量，λ0为投影光栅节距，θ0为原点O的相位。

　　2.2单双目重建技术

　　传统的求解参数a1~a8的方法是先通过平面标定板对单目相机进行标定，再对投影到标定板上的光栅进行解相，得到样本点集（Xc,Yc,Zc,θ），带入式（3），可得到一组以参量a1~a8为未知数的线性方程，解方程组，即可得到参量值。

　　本节提出了一种基于双目点云重建单目点云的方法，直接将双目重建的点和对应的相位值组成样本集（Xi,Yi,Zi,θi）代入式（3），优化解得a1~a8，然后对于仅在单个相机视场内有效的物点，将其相位值代入式（3），结合式(1)中X、Y和Z的关系计算三维坐标。相比传统的参数求解方法，本方法既消除了传统方法中由于相机标定和光栅解相带来的误差，提高了参数的优化精度，又简化了操作过程。

　　设左相机为参考坐标系，计算左单目点云时可以直接使用双目点和左相位场，但计算右单目点云时，将双目点云转换到右相机坐标系下，加上右相位场来计算，最后再将右单目点云坐标统一到左相机坐标系下。算法实现的步骤如下：

　　（1）标定：使用张正友平板标定法［12］对双目系统的内外参数进行标定。

　　（2）相位解算：先使用最大类间方差法分离物体和背景，将属于物体部分的点标记为有效点，再通过四步相移［13］加多频外差［14］解算出左右相位场。

　　（3）匹配：利用相位值相等和极线约束条件寻找左右相机中的对应匹配点，同时在相位图中对未匹配点予以标记，再进行亚像素插值提高精度。

　　（4）双目重建：得到左右相机的匹配点后，利用相机的内外参量，根据三角原理法计算三维坐标。

　　(5) 左右单目重建：分别利用左右相机与投影仪组成两个单目测量系统。利用本文所述的单目测量方法分别对左右相机中的未匹配点求取对应的三维坐标，并统一到双目测量坐标系中。

　　为了避免单目测量系统重建双目缺失区域以外的部位，在双目测量匹配过程中，分别对左右相机中的未匹配点进行标记，对相位图中的每一点设置一个标记值，如果能够找到对应匹配点则设其标记值为1，否则为0，在后续的单目重建中仅对标记值为0的点进行处理。

3实验验证及结果分析

　　实验采用基于双目视觉的数字光栅投影系统，该系统由两个高分辨率（分辨率1 280×1 024）的工业CCD相机和一个DLP投影仪组成，测量时使用投影仪向被测物体投射一组光强呈正弦分布的光栅，左右两个相机进行同步采集受物体表面调制后的光栅，然后根据采集的图像，获取其相位信息最后根据标定参数，应用三角测量原理获得物体表面三维数据。

　　飞机模型的点云如图3所示。　

　　在图3中，单次扫描重建的点云如图3（b)所示，在机身和两侧机翼交接的地方会出现一些空洞,其原因是由于机身的遮挡, 而不能被双相机同时拍摄到，因此出现点云缺失的空洞。分别基于双目点云及其相位场优化得到的a1~a8见表1。单目重建也对双目无法测量的部位进行了补充，使单次测量结果更加完整。图3（d)中仍然存在的一些空洞是物体表面的黑色斑点所致，与本文算法无关，可以通过向物体表面喷白色显影剂的方式来测得。

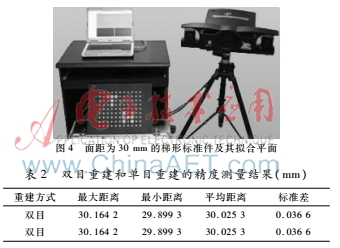
　　为了对本测量系统的重建精度进行评估，对面距为30 mm的梯形标准件进行测量，如图4所示，将得到的点云拟合成平面，计算两平面之间的面距，测量结果如表2所示，可以看出单目点云精度比双目点云稍低，可以用于对精度要求不是很高的场合。

　　单目重建算法能对双目点云中的测量空洞进行补充，但其精度往往达不到双目点云的精度，由于单目重建是直接通过相位值计算物点的三维坐标，相位误差是影响单目测量精度的主要因素，由投影仪的Gamma非线性和工业相机的非线性响应共同引起的光栅图像非正弦化是相位误差的主要来源，相机采集图像时引入的环境光与相机Gamma值共同作用也会使采集的光栅图片非正弦化。

4结论

　　本文提出了一种基于相位高度模型的新单双目重建方法，使用双目点云优化出系统参数用于单目点云的计算。该方法能在单次扫描过程中同时实现单目和双目的点云计算，对双目测量结果中出现的空洞区域，可以使用该处单目测量的结果加以补充。这种方式的单目重建在双目视觉系统的基础上，无需增加其他硬件设备或者操作步骤，简单可行。与单纯地依靠双目测量系统相比,使用此方法能够有效地改进系统的测量范围和提高测量结果的完整性。

　　单目重建算法能对双目点云中的测量空洞进行补充，但其精度往往达不到双目点云的精度。由于单目重建是直接通过相位值计算物点的三维坐标，因此需要进一步提升相位精度。下一步的重点是研究相位误差补偿方法，建立相机和投影仪Gamma值的数学模型，利用预编码方法消除相位误差。

参考文献

　　［1］ Zhang Zonghua, TOWERS D P, TOWERS C E. Snapshot color fringe projection for absolute 3D metrology of video sequences［J］. Applied Optics, 2010, 49: 5947-53.

　　［2］ Dai Meiling, Yang Fujun, He Xiaoyuan. Singleshot color fringe projection for threedimensional shape measurement of objects with discontinuities［J］. Applied Optics, 2012, 5(12): 2062-2069.

　　［3］ Wang Yongchang, Liu Kai, Hao Qi, et al. Period coded phase shifting strategy for realtime 3D structured light illumination［J］. IEEE Transactions on Image Processing, 2011, 20(11): 3001-3013.

　　［4］ GORTHI S S, RASTOGI P. Fringe projection techniques: whither we are?［J］. Optics & Lasers in Engineering, 2010, 48(2): 133-140.

　　［5］ TYAGI A, POTAMIANOS G, DAVIS J W, et al. Fusion of multiple camera views for kernelbased 3D tracking［C］. IEEE Workshop on Motion and Video Computing. Austin, TX, USA: IEEE Press, 2007:1-8.

　　［6］ IKEMURA S, FUJIYOSHI H. Realtime human detection using relational depth similarity features［J］. Computer Vision–ACCV 2010, Springer Berlin Heidelberg, 2010,6495: 25-38.

　　［7］ MA Y, WORRALL S, KONDOZ A M. Depth assisted visual tracking［C］.  10th Workshop on Image Analysis for Multimedia Interactive Services, 2009. WIAMIS'09. IEEE, 2009: 157-160.

　　［8］ Jin Xin, Chen Xiaowu, Zhou Bin, et al. Cooperatively resolving occlusion between real and virtual in multiple video sequences［C］. 2011 Sixth Annual IEEE China Grid Conference (China Grid), 2011: 234-240.

　　［9］ 耿英楠.立体匹配技术的研究［D］.长春：吉林大学,2014.

　　［10］ 许雯.立体视觉中局部立体匹配算法研究［D］.西安:西安电子科技大学，2014.

　　［11］ 盖绍彦，达飞鹏.一种新的相位法三维轮廓测量系统模型及其标定方法研究［J］.自动化学报, 2007,33(9)：902-910.

　　［12］ ZHANG Z. A flexible new technique for camera calibration［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000. 22(11): 1330-1334.

　　［13］ 蔡长青,贺玲凤.基于四步相移的相位差提取方法［J］. 华南理工大学学报（自然科学版）,2011,39(9):93-96.

　　［14］ 陈松林,赵吉宾,夏仁波.多频外差原理相位解包裹方法的改进［J］.光学学报,2016,36(4):1-11.