张芝贤，程继坤，武旭娟

　　（沈阳航空航天大学 电子与通信工程学院，辽宁 沈阳，110136）

       摘要：双目立体视觉测量系统是工业测量中的重要手段，三维重建是双目立体视觉测量体统中非常重要的一环。基于视差原理的传统三维重建模型是对双目立体视觉系统的一种理想化抽象。通过分析由平面到三维点的实际映射过程，提出了一种更加符合实际数据的三维重建模型，异面直线公垂线三维重建方法。该方法通过计算两摄像机光心与其各自像点构成的两条空间直线的公垂线，即两条异面直线的最小距离点来定位三维空间点，且其最小距离参数可有效判断误匹配点。通过实验对该方法进行了验证。结果表明该方法可达到传统视觉三维重建方法的测量精度，并可有效判断匹配点是否为误匹配点。

　　关键词：双目立体视觉测量；异面直线公垂线；误匹配点；三维立体重构

　　中图分类号：TP391文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.04.024

　　引用格式：张芝贤，程继坤，武旭娟.公垂线法双目立体视觉三维重建［J］.微型机与应用，2017,36（4）：80-83.

0引言

　　双目立体视觉测量是一种基于视差原理的三维非接触测量技术。由两台摄像机在不同的角度下同时获取待测目标的图像，然后利用特征点的图像坐标根据测量模型重建其三维坐标，最后通过拟合这些特征点获取待测目标的三维几何信息。双目立体视觉重建技术已经深入到人们生活、生产和工作的方方面面，具有重要的理论意义和实用价值。它所涉及的知识面很广，是一种综合性的技术，有广阔的发展前途和广泛的应用前景［1］。在三维立体重构中,空间点作为三维结构最为基本的组成单位，在理论方面能够从点构成线，从线构成面，随后通过各个面来形成三维空间结构。所以，测量空间点的具体坐标是最为基本的双目立体视觉内容。双目立体三维重构也是基于点的三维信息的获取。

　　双目立体视觉利用三角几何相关原理来对视差进行计算进而获得物象在三维空间上的信息［2］。为理解双目立体的视觉原理，通常假设存在一个结构非常简单的双目视觉系统［3］，两个摄像机光轴平行并且它们的内参完全相同，如图1所示。这个系统的基线（两个摄像机光心之间的连线）与第一个摄像机的x轴一致。

　　而对于构建一般双目视觉系统，无法严格保证两相机坐标系严格平行。一般测量模型［4］更便于理解双目立体视觉结构。如图2所示，该模型不需要两个相机坐标系严格平行。

　　对于以上两种测量模型，都首先需要进行标定获得相机的内外参数，区别在于理想测量模型需要根据内外参数将测量系统映射转化为理想测量系统，而一般测量模型仅需要对图像做畸变校正，而后直接利用两相机的相对位姿关系求得三维点信息。

　　然而由于实际的镜头并不是理想的透视成像，而是带有不同程度的畸变，图像中存在噪声的干扰影响特征点提取精度等原因，使得空间点所成的像并不是在线性模型所描述的位置，在实际数据中这两条直线并非交于一点而是构成空间异面直线。另一方面，对于匹配错误的同名点，以上两种算法的重构过程无法判断该组同名点是否匹配有误。而误匹配在所有的匹配算法中都是无法完全避免的［5］。由于误匹配点的不确定性可能会导致重构三维空间点严重偏离实际点，大大影响了系统测量精度。

　　根据双目立体视觉的实际数据，在一般测量模型基础上，可将两条视线即两相机光心与各自像点的连线视为两条空间异面直线。通过求取这两条异面直线以及异面直线公垂线［6］，可确定三维重构点的最佳估计位置，同时可根据距离参数判断该点是否为误匹配点。

1公垂线法三维立体重建

　　1.1摄像机标定与点的坐标系转换

　　图像与三维信息之间的对应关系是由摄像机成像的几何模型决定的,这些几何模型参数就是摄像机参数,求解摄像机参数的过程即摄像机标定的过程［7］。摄像机标定是双目立体视觉系统中的重要一环，是三维立体重构的基础环节。通过摄像机标定一方面获得成像几何模型的结构参数用于三维立体信息的重构，另一方面是对摄像机存在的镜头畸变进行校正确保测量精度。

　　研究中采用张正友提出的基2D平面标定板的标定算法［8］，并在其原有算法仅考虑镜像畸变基础上考虑了切向畸变带来的影响，使得畸变校正结果更理想，精度更高。

　　其中，k1、k2为径向畸变系数，p1、p2为切向畸变系数，pd(xd, yd)为实际的图像坐标，pu(xu, yu)为不考虑镜头畸变的线性模型下的图像坐标，即为畸变校正后的图像坐标。

　　标定获得相机的内部参数以及两相机坐标系间的变换关系H。根据内参可以确定相机光心与像点在各自坐标下的坐标，然后根据两相机坐标系的转换关系H将所有点统一到同一坐标系下［9］。这里根据方程(2)将所有三维点统一到左相机坐标系下。

　　其中PR为空间点在右相机坐标系下的空间坐标，PL为空间点在左相机坐标系下的坐标R为旋转矩阵，t为右相机坐标系到左相机坐标系的一个平移量。

　　由此可由一对同名点以及相机各自光心四个点构成双目立体视觉的两条视线，并可将这两条异面直线在同一坐标系下表示。

　　1.2公垂线法立体重构

　　如图3所示，两条视线构成一对异面直线。空间异面直线的最小距离点即为两条异面直线的公垂线与两条异面直线的交点。这里是以左相机坐标系为作为系统坐标系。因此选取左相机的视线与公垂线的交点为三维重构的最佳估计点。

　　根据P1、O1与P2、O2构成的两条视线的直线为：

　　公垂线两视线的交点分别为：

　　M(x1+m1t1,y1+n1t1,z1+p1t1)

　　N(x2+m2t2,y2+n2t2,z2+p2t2)

　　两条异面直线的最小距离参数：

　　选取左相机视线与公垂线交点M为最佳三维重构点。距离参数Dist为两条视线的最小距离。

　　与传统方法相比公垂线法立体重构除获得三维重构点外，还可获得一个异面直线距离参数。在理想情况下两个特征点匹配正确时该距离参数为零。而实际中匹配正确的也会存在微小的位置偏差，但这种偏差基本是亚像素级的，虽然会使距离参数不为零，但其值在会在一个很小的范围之内。当重构点为误匹配点时，匹配点对的误差则是不可预知的，至少是像素级别的，其可能是几个、几十个甚至上百个像素点，因而距离参数数值也急剧增大。正是因为正确匹配点与误匹配点在距离参数数值上的差异，所以可将该值作为对误匹配点进行甄别的一个有效手段。

2三维重构实验及精度评价

　　本文标定过程采用宽度为500 mm的 Halcon标定板对双目立体视觉系统进行标定。标定获得相机内参如表1、表2所示，左右两相机的相对位置关系如表3所示。

　　实验中标定板精度在1 μm以内，因此通过提取标定板中的标志点进行匹配三维重构来验证公垂线三维重构点的距离精度。实验中拍摄了标定板8种不同姿态，并对距离为375 mm的两标志点进行三维重构，如图4所示。

　　利用不同三维重构算法对该对同名点进行三维重构求取距离，并对三种方法进行精度分析对比，如表4所示。利用公垂线法三维重构同时可获得16个点重构的距离参数Dist。而后在在双目系统下利用匹配算法进行特征点的提取与匹配，通过人工识别找出自动匹配点对中的误匹配点。同样对重构获得距离参数Dist，并将与正确匹配点对的距离参数作比较，如表5所示。

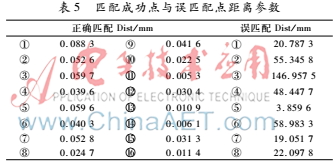
　　由表5可知，正确匹配点与误匹配点对距距离参数Dist有明显差异,且其值与系统精度重构一致，在10-5 m波动。而误匹配点由于误匹配的随机性则距离参数具有较大波动性，并且其距离参数要远远大于求取正确匹配点的距离参数，所以根据该依据可有效区分匹配点中的误匹配点。

3结论

　　本文基于传统双目立体视觉重构方法提出了一种新公垂线双目立体视觉重构方法。通过实验验证了该方法可达到传统的三维立体重构方法对空间点的重构精度。同时利用该方法三维点重构过程中获得的异面直线的距离参数来对匹配点进行判断。通过设置合适阈值可自动筛选出重构点中的误匹配点将其去除，不仅可提高测量效率，而且进一步保证了测量精度。

参考文献

　　［1］ FUSIELLO A.Uncalibrated euclidean reconstruction:a review［J］.Image and Vision Computing, 2000, 18(67): 555563.［2］ 马颂德,张正友. 计算机视觉计算机理论与算法基础［M］.北京: 科学出版社,1998.

　　［3］ 马桂珍,谌海新,马丙辰.基于双目视觉的手术器械跟踪定位技术［J］.微计算机应用,2005,26(2)：181183.

　　［4］ 邾继贵,于之靖.视觉测量原理与方法［M］.北京：机械工业出版社，2011.

　　［5］ 刘晶晶.基于双目立体视觉的三维定位技术研究［D］.武汉:华中科技大学,2007.

　　［6］ 吕林根,许子道.解析几何［M］.北京:高等教育出版社,2007.

　　［7］ 贾云得.机器视觉 ［M］.北京：科学出版社,2005.

　　［8］ Zhang Zhengyou. A flexible new technique for camera  calibration ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence,2000，22（11）：1330 1334.

　　［9］ STEGER C,ULRICH M,WIEDEMANN C.机器视觉算法与应用［M］.杨少荣，吴迪靖，段德山，译.北京：清华大学出版社，2008．

　　［10］ LENZ R K,TSAI R Y. Techniques for calibration of the scale factor and image center for high accuracy 3D machine vision metrology ［C］. Proceedings of IEEE International Conference on Robotics and Automation, Washington DC：IEEE，1987：6875.