杜青
(南京工程学院 计算机工程学院,江苏 南京 211167)
摘要:本文以C++语言设计了大整数类,在类中以数组存储大整数,同时借鉴分治算法思想实现了大整数的乘法运算。算法中将被乘数与乘数按照相同位数进行分组,通过对每组较小数值整数进行乘法和加法运算而得到大整数相乘的积。该程序在VC++2015开发平台调试通过。测试结果表明,当每个分组数据位数多时,运算速度显著提高。
关键词:大整数;大整数相乘;分治算法;类
中图分类号:TP301文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.02.003
引用格式:杜青.基于类的大整数乘法运算的实现[J].微型机与应用,2017,36(2):8-9,13.
0引言
大整数是指数值很大、超出计算机整数表达和处理范围的非负整数。一般计算机能够处理的整数有三种类型,即2字节(16 bit)、4字节(32 bit)和8字节(64 bit)整数,其中8字节整数取值范围最大,8字节无符号整数取值范围是:0~264-1。当整数值超过整数范围的最大值264-1时,计算机无法直接处理。
大整数的乘法运算在密码学等领域有着广泛的应用。如著名的公钥加密算法RSA算法,大整数相乘是其中必不可少的运算,由于运算中使用的密钥推荐位数为1 024位,为了达到更高安全级别,密钥长度甚至达到上万位,远远超出计算机所能直接处理的64 bit的整数范围。
当需要对大整数进行乘法运算时,面临的问题是:如何存储大整数以及如何提高大整数乘法的运算速度。已有的实现大整数乘法的程序中,有的采用累加的方式,将被乘数重复相加若干次,累加的次数等于乘数;有的按照手算的形式,将乘数逐位与被乘数相乘,并将结果做位移运算后按位求和[1]。当被乘数与乘数位数很多时,这些方法运算时间长。
本文以C++语言设计了一个大整数类,在类中以数组存储大整数,同时借鉴分治算法的思想[2],将数值很大的大整数分解为若干组数值较小的整数,通过对每组较小数值整数的运算得到大整数相乘的积。程序在VC++2015开发平台调试通过。
1大整数的存储
由于大整数位数多,若用字符串形式表示,在做运算时,首先要将表示大整数的字符串转换成数值。转换时考虑到大整数的数值一般超出整数的取值范围,所以采用整型数组存储其值[3]。
以下给出了大整数类BigInt的声明,类中的数据成员uint64_t 类型数组array用于存放大整数,uint64_t是64 bit无符号整数类型。转换时从大整数字符串最低位开始,每K个字符为一组,最高位不足K个字符时补0,将每组字符转换为一个数值较小的整数,每个较小整数存放到整型数组的一个元素中。类中数据成员n为已存放了数据的元素个数,即分组数。类声明代码如下:
#define N 10000//数组大小
#define K 3//每个分组中包含的字符个数
class BigInt
{public:
BigInt();//无参构造函数,将n置0
BigInt(string str);//转换构造函数
int compare(BigInt num); //比较类对象大小
friend BigInt operator*(BigInt num1, BigInt num2);//重载乘法运算符
friend int operator>(BigInt num1, BigInt num2);
//重载大于运算符
private:
uint64_t array[N];//存放大整数的数组
int n;//存放了数据的元素个数
};
类中的转换构造函数实现了将大整数字符串分组,并将各组字符串转换为数值存放到array数组中的操作。转换构造函数的代码如下:
BigInt::BigInt(string str) //将字符串转换为数值
{int end = str.length() - 1, i;
uint32_ttemp,w;//w代表权重
n = 0;
i = end;//从最低位开始处理
while (i >= 0)
{temp = 0;w = 1;
for (int k =0;k<K;k++) //K个字符组成1个数
{if (str[i] >= 0&&str[i] <= 9)
{temp = temp + w*(str[i] - 0);
w *= 10; i--;
if (i<0)break;
}
}
array[n] = temp;n++;
}
for (i = n;i<N;i++) array[i] = 0; //其他元素置0
}
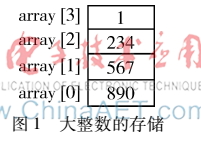
当K=3时,字符串“1234567890”在数组array中存放的形式如图1所示。
2大整数乘法的实现
2.1大整数乘法的算法
当一个m位的大整数X与一个n位的大整数Y相乘时,如按照手算的方式进行计算,需要将Y的每一位与X的每一位相乘,共要做m×n次数据相乘。如m、n很大,则数据相乘次数多,从而使整个乘法运算时间长。
为了解决这个问题,利用分治法的思想,将X、Y均分解为K位一组的整数[4],即X分解为…xi…x2x1x0,共(m+K-1)/K组数字,Y分解为…yj…y2y1y0,共 (n+K-1)/K组数字,运算时将由Y分解得到的每一组整数yj与由X分解得到的每一组整数xi相乘。
以K=3时,1234567890与1234567890做乘法运算为例,如按手算方式进行运算,需做10×10共100次数据相乘,而若将被乘数与乘数分解为3位一组的数字,即各自分解为4组数字,如图2所示,则只需要完成4×4共16次数据相乘,数据相乘次数大大减少。在进行分组数据相乘后,再按组进行数据相加,从而得到两个大整数乘法运算的积。大整数分组运算过程示意图如图2所示。

当K较大时,每组数据因位数增加而数值变大,分组数目随之减少,分组数据乘法次数也减少。但当K过大时,每组数据与其他组数据相乘时得到的中间结果可能会超出整型数据的最大值而导致数据溢出。为了防止溢出情况的出现,K的取值不能太大。由于uint64的最大值是264-1,因此每组数字的最大值不能超过232-1,即4 294 967 295,由此推断,每组数字不能超过9位,即K要满足:1≤K≤9。
2.2大整数乘法的实现
m位的大整数X与n位的大整数Y进行乘法运算时,将yj依次与xi相乘,保留xi*yj%BASE为中间结果,yj*xi/BASE为进位,其中BASE的值等于10K,是运算的基[5]。两个大整数相乘后得到的乘积的位数是m+n或m+n-1[6]。
下面给出了实现大整数乘法运算的函数定义,该函数是乘法运算符重载函数,已在BigInt类中声明为友元。该函数代码如下:
#define BASE 1000 //运算的基
BigInt operator*(BigInt num1, BigInt num2)
{BigInt temp1, temp2;
if (num2>num1)//保证被乘数大于乘数
{temp1=num1; num1=num2; num2=temp1;}
uint64_t num, c;//num存放中间结果,c为进位
int maxi, mini, i, j;
maxi = num1.n; //被乘数分组数
mini = num2.n; //乘数分组数
for (i = 0;i<mini;i++)
{c = 0;//进位初值为0
for (j = 0;j<maxi;j++)
{num = num1.array[j] * num2.array[i] + c;
temp2.array[j+i]+=num%BASE; //做一次
//分组相乘之后做分组加法
c = num / BASE;
if (temp2.array[j + i] >= BASE)//判断是
//否超出BASE
{temp2.array[j+i]=temp2.array[j+i]%BASE;
c++;//进位加1
}
}
if (c) temp2.array[j + i] += c; //有进位时
}
temp2.n = maxi + mini - 1;//设置乘积的分组数
if (c) temp2.n++; //最后一次运算有进位时
return temp2;
}
以上实现大整数乘法的函数中,做一次分组数据相乘之后,将得到的中间结果做分组加法运算,并且在做分组加法运算时,要判断加法运算的结果是否溢出,若溢出,将加法运算结果对BASE取余数,同时进位加1。
2.3运行测试
在VC++2015开发平台运行程序,测试时用两个4 000位大整数做乘法,且使该乘法运算重复执行1 000次,测试当K取1、2、3、……、9不同值时所花费时间,得到结果如表1所示。由表1可以看出,K值增大,大整数乘法运行时间大大减少。

3结论
本文以C++类的方式实现了大整数的乘法运算,算法中根据分治法思想,将被乘数与乘数按照相同位数进行分组,通过对每组较小数值整数进行运算,从而得到大整数相乘的结果。该程序在VC++2015开发平台调试通过。实验结果表明,当每个分组数据位数多时,乘法运算速度显著提高。
参考文献
[1] 周健,李顺东,薛丹.改进的大整数相乘快速算法[J].计算机工程,2012,38(16):121-123.
[2] 王晓东. 计算机算法设计与分析(第3版)[M]. 北京:清华大学出版社, 2014.
[3] 杨灿,桑波.大整数乘法运算的实现及优化[J].计算机工程与科学,2013,35(3):183-190.
[4] 王念平,金晨辉.用分治算法求大整数相乘问题的进一步分析[J].电子学报,2008,36(1):133-135.
[5] 李文化,董克家.大整数精确运算的数据结构与基选择[J].计算机工程与应用,2006,42(32):24-26.
[6] 刘觉夫,周娟.大整数运算的基选择[J].华东交通大学学报,2007,24(2):100102.

