郭江1,2,肖宇峰1,2,刘欣雨1,陈丽1
(1.西南科技大学 信息工程学院,四川 绵阳 621010;2.西南科技大学 特殊环境机器人技术四川省重点实验室,四川 绵阳 621010)
摘要:移动机器人路径规划一直是移动机器人领域里的重要技术问题。A*算法在最优路径搜索上有着比较成功的运用,但在栅格环境下的A*算法也存在着折线多、转折角度大等问题。在考虑移动机器人的实际工作环境及相关运动参数后,这些问题都将大大地影响移动机器人的工作效率。在对以上问题进行分析后提出了一种基于Bezier曲线与A*算法融合的方法来实现移动机器人的路径规划,再通过MATLAB、VREP仿真工具来实现Bezier_A*融合算法与平滑A*算法及A*算法的对比。通过Bezier_A*融合算法使得机器人在工作中的寻优能力、路径规划效率都得到较大的提高。
关键词:移动机器人;路径规划;A*算法;Bezier曲线;融合算法
中图分类号:TP391文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.02.017
引用格式:郭江,肖宇峰,刘欣雨,等.Bezier曲线与A*算法融合的移动机器人路径规划[J].微型机与应用,2017,36(2):52-55,59.
0引言
*基金项目:国家自然科学基金(61601381);四川省科技支撑计划项目(2015GZ0035);四川省教育厅重点项目(14ZA0091)移动机器人路径规划问题一直以来都是移动机器人研究的热点和难点[1]。在近年的发展中,越来越多的学者和专家已经致力于结合智能控制算法来解决移动机器人的路径规划问题。例如遗传算法[2]、蚁群算法[3]、禁忌搜索算法[4]等智能算法及其混合形式都被用来解决路径规划问题。但这些智能算法目前还不太完善,存在着一些缺点,例如遗传算法编码长度变化范围大,求解规模小;Dijkstra算法[5]直接搜索全局而不考虑目标信息,导致路径求解时间长,难以满足快速规划路径的需求;D*算法[6]主要解决局部的动态路径规划问题。
A*算法[7]作为一种比较成功的全局路径规划算法,已成功应用于机器人的路径寻优和规划方面,并且取得良好的路径规划效果。但由于A*算法本身的计算特点,在栅格环境下A*算法规划出的移动机器人路径一般存在着折线多、累计转角大等问题。在对A*算法进行平滑[8]处理方面,最近几年也出现了不少的研究成果。但绝大多数的平滑处理方法都是着眼于障碍物与移动机器人交汇处来进行处理。这种平滑方式有着很大的局限性,平滑算法在对路径平滑时,都是遍历所有的节点,当某一个节点前后节点连线上无障碍物时,就将延长线路的这一中间节点删除,当遍历到路径上从起始点到终止点的所有节点时,平滑算法终止,路径平滑规划结束。这样的平滑方式由于是遍历所有的节点,将大大影响算法的运行效率。本文主要处理两个问题:其一,因A*算法在栅格地图中生成的路径折线多、转折多而影响机器人工作效率的问题;其二,现行的路径平滑算法效率不高的问题。针对以上两个问题,本文提出一种将Bezier曲线[9]与A*算法融合的规划算法,并通过MATLAB、V_REP仿真工具来实现与平滑A*算法、A*算法的性能对比分析。
1环境建模
移动机器人的路径规划在实际应用上主要是面对两个问题:一是环境建模;二是路径搜索生成及处理策略[10]。本节主要讨论环境建模,在下一小节将对路径搜索算法及处理策略进行分析。
移动机器人路径规划的环境建模有很多种,例如栅格法、拓扑图、几何信息法等。栅格法在许多机器人系统中得到应用,是比较成功的一种环境建模方法,且栅格地图容易创建和维护,因此本文采用栅格法。常用的环境地图表示中栅格地图的特点是容易创建和维护,创建成本和使用成本都比较低。移动机器人所了解的每个栅格信息直接与环境区域相对应,且移动机器人可以根据栅格地图进行导航与定位。在本文中所创建的栅格环境模型是根据实验室环境及障碍物映射生成的,最终栅格通过机器人仿真工具VREP画出,如图1所示。VREP栅格地图中,黑色区域表示实验室中的障碍物区域,灰白色区域表示可安全行走区域。
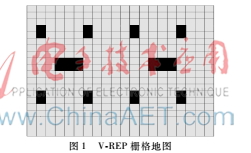
2Bezier曲线与A*算法原理分析
2.1A*算法原理分析
A*算法是建立在Dijkstra和BFS(广度优先搜索)算法基础上的搜索算法。它的整体框架采用遍历搜索法,但是它采用了启发函数来估计地图上任意点到目标点的费用,从而可以很好地选择搜索方向。
A*算法引入了当前节点x的启发函数f(x),当前节点x的启发函数定义为:
f(x)=g(x)+h(x)(1)
其中g(x)是从起点到当前节点x的实际费用度量,h(x)是从当前节点x到终点的最小费用估计。h(x)只要满足相容性条件:不能高于节点x到终点的实际最小费用,则原问题存在最优解,并且A*算法一定能够求出最优路径。A*算法的优点是利用启发函数,使搜索方向更加智能地趋向于终点,所以其搜索深度较小,搜索的节点数少,这样将大大提高算法的运行效率。
A*算法是广泛使用的移动机器人路径规划上的一类算法,同时它也适用于全局环境信息已知的路径规划。但是目前A*算法在实际的工程运用中还是存在折线多、转折次数多、累计转角大等问题,给机器人运行造成较大的麻烦,例如,转角多时,必须准确计算出机器人和障碍物间距,否则就会发生碰撞;当累计角度大、转角多时,机器人的工作效率也会下降。考虑上述问题,本文首先采用A*算法实现路径的初步规划,再采用Bezier曲线实现融合处理。
2.2Bezier曲线分析
n次曲线的定义式有多种形式,目前使用最广泛的是由英国学者Forrest于1972年给出的定义:
P(u)=∑niPiBi,n(u),u[0,1](2)
其中,pi(0≤i≤n) 被称为曲线的第i个控制点,顺次连接从p0到pn的折线被称为Bezier曲线的控制多边形。Bi,n(u)为n次Bernstein多项式,其表达式为:

在坐标系xoy中,对于给定已知的四个控制点(x0,y0),(x1,y1),(x2,y2),(x3,y3)可以由公式(4)、(5)确定一个3次Bezier曲线。
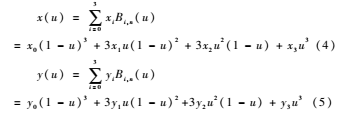
通过分析3次曲线的定义式可知,0次Bezier曲线是其唯一的控制点P0,1次Bezier曲线是连接P0至P1的线段,2次或者2次以上的Bezier曲线则具有以下性质:
(1)端点性质:Bezier曲线的起点P0和终点Pn与特征多边形的起点和终点重合。
(2)切矢量性:Bezier曲线的起点和终点处的切线方向和特征多边形的第一条边及最后一条边走向一致。
(3)凸包性:曲线落在特征多边形各顶点构成的凸包之中。
(4)几何不变性:Bezier曲线的几何特性不随坐标变化而变化,Bezier曲线的位置和形状与特征多边形顶点的位置有关,而不依赖坐标的选择。
通过以上两个算法的分析,下面将设计Bezier曲线与A*算法的融合方案。
2.3Bezier曲线与A*算法融合的路径规划方案
移动机器人路径规划的最终目标是:在保证机器人能达到目标点的同时,找到一条平滑可行的最短路径。移动机器人路径规划的一切设计方案都应该遵循这个宗旨。A*算法能够保证机器人在充满障碍物的地图中找到一条最短路径。但找到这一条最短的路径还是远远不够的,A*算法本身存在着许多的不足:在栅格环境下A*算法规划出的移动机器人路径往往存在着折线多、转折次数多、累计转折角度大、运行效率低等许多问题。
在分析了A*算法的突出问题后,提出了一种A*算法与Bezier曲线融合的路径规划方法,通过融合算法的实现,将有效地解决A*算法及平滑A*算法所存在的折线多、转折次数多、转折角度累计大等问题。整个融合算法大体分以下步骤完成:第一步,实现A*算法对移动机器人路径的初步规划;第二步,将所规划的路径进行Bezier曲线再规划处理;第三步,对Bezier曲线融合后的分段曲线进行拼接并最终输出融合路径。在以上的三个处理步骤中主要的难点问题是如何解决A*算法初次规划后,对初步路径的节点信息进行再处理。当得到初步的路径节点信息后,不可能对所有节点都采取一致的3次Bezier曲线或者2次Bezier曲线优化,单调地使用2次或者3次以及更高次的Bezier曲线处理往往会使移动机器人陷入障碍物死区,如图2所示,在对4个节点进行Bezier曲线优化时,触碰到了障碍物,让机器人陷入了工作死区。但对于障碍物死区问题,结合2次或者3次的处理后,问题将得到很好的解决,能使移动机器人成功地避开障碍物死区。对于2次的Bezier曲线,由公式(2)可得:

结合2次曲线和3次曲线的处理,即可避免移动机器人陷入死区等问题。再对每一段k(k=1,2,3)次曲线按照公式(8)进行拼接:
S(u)=∑ki=0(Pi-Bi(ui))2(8)

如图3所示,通过分段的Bezier处理,有效地避免了障碍物死区问题。整个融合算法实现伪代码如下:
OPEN表 = 起始点start;
CLOSED 表 = 空;
BEZIER 表 = 空;
图3融合算法避开死区
While(OPEN != NULL)
{
从OPEN表中取估价函数f最小节点n;
If(n==目标节点){
Break;
}
For(当前节点n的每个子节点X){
算X的估价值;
If(X in OPEN){
If(X的估价值小于OPEN的估价值){
把n设置为X的父节点;
更新OPEN表中的估价值;
}}
If(X in CLOSE){
If(X的估价值小于CLOSE表估价值){
把n设置为X的父节点;
更新CLOSE表中的估价值;
把X节点放入OPEN;
}}
If(X not in both){
把n设置为X的父节点;
求X的估价值;
并将X插入OPEN表中
}}//end for
将n节点插入CLOSE表中;
按估价值将OPEN表中的节点排序;
BEZIER 表 = 初次规划的路径节点;
}//end while(OPEN != NULL)
While(BEZIER != NULL){
For(对路径所有节点进行Bezier处理){
If(4节点处理无障碍){
3次bezier曲线处理;
更新此4节点为一段Bezier曲线;
}
If(3节点处理无障碍){
2次Bezier曲线处理;
更新此3节点为一段Bezier曲线;
}
If(2节点处理无障碍){
1次Bezier曲线处理;
更新此2节点为一段Bezier曲线;
}}//end for
对每段Bezier曲线实现拼接处理;
输出融合处理后的路径
}//end while(BEZIER !=NULL)
3实验仿真分析
本仿真实验计算机采用处理器为Intel(R) Core(TM) i54595,内存为4 GB;算法分析工具为MATLAB;路径规划仿真工具为VREP。
通过机器人仿真工具VREP,编写相关代码实现了A*算法及Bezier_A*融合算法的路径规划如图4、图5所示。从两个图中可以很清晰地看到,A*算法规划路径的折线较多、转折次数也较多,但在图5中由Bezier_A*融合算法生成的路径上折线和转角已经大大减少。

在V-REP中将A*算法及融合算法的节点数据导出到数据表格,在MATLAB中,得到图6所示的规划路径。
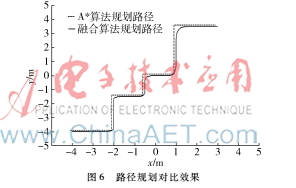
图6路径规划对比效果为同其他的路径规划算法形成性能分析对比,本文将文献[7]和[8]中给出的A*算法、平滑A*算法两种算法的分析结果与本文算法进行对比分析,对比环境为:40×40的栅格地图。表1是Bezier_A*融合算法与A*算法性能对比,表2是Bezier_A*融合算法与平滑A*算法的性能对比。
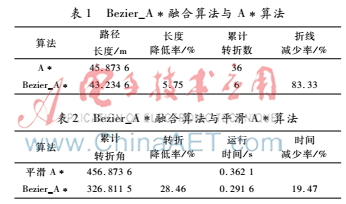
降低率/%累计
转折数折线
减少率/%A*45.873 636Bezier_A*43.234 65.75683.33
表2Bezier_A*融合算法与平滑A*算法算法累计
转折角转折
降低率/%运行
时间/s时间
减少率/%平滑A*456.873 60.362 1Bezier_A*326.811 528.460.291 619.47
通过仿真实验可以得出,与A*算法、平滑A*算法相比,使用Bezier_A*融合算法所规划的移动机器人路径各方面性能得到了较大的提升。对比A*算法,Bezier_A*融合算法有效地减少路径距离6%左右,将累计的转折数减少了85%左右;对比平滑A*算法,Bezier_A*融合算法能更加有效地减少累计转折角30%左右,并且将算法的运行效率提升了20%左右。
4结论
本文主要针对栅格环境中的移动机器人路径规划实现,分析了A*算法、平滑A*算法在移动机器人路径规划上所存在的缺点,如转折角度大、转折数多等问题,这些问题都将大大影响移动机器人的实际工作效率。针对以上问题,本文提出A*算法与Bezier曲线融合的路径规划算法,融合算法大大改善了移动机器人的运动性能。最后通过仿真实验证明,融合算法减少了累计转折角30%左右,减少累计转折数85%左右,相比于一般的平滑A*算法,融合算法还提升了运行效率。实际运用中Bezier_A*融合算法在障碍物分布广泛的栅格环境下具有转折次数少、累计转折角度小等优点,更能满足移动机器人在工作时的运动需求。
参考文献
[1] ZAMIRIAN M,KAMYAD A V,FARAHI M H. A novel algorithm for solving optimal path planning problems based on parametrization method and fuzzy aggregation[J].Physics Letter A,2012,373(38):34-39.
[2] PANDA R K, CHOUDHURY B B. An effective path planning of mobile robot using genetic algorithm[J].IEEE International Conference on Computational Intelligence & Communication Technology,2015,145(15):287-291.
[3] 张琦,马家辰,谢伟,等. 基于改进蚁群算法的移动机器人路径规划[J]. 东北大学学报,2013,34(11):1522-1527.

