凡旭国1,2,周金治1,2,高磊1,2
(1.西南科技大学 信息工程学院,四川 绵阳 621010; 2.特殊环境机器人技术 四川省重点实验,四川 绵阳 621010)
摘要:锂离子电池管理系统设计及荷电状态(SOC)估算依赖于电池等效电路模型的建立,在几种常见的动力锂离子电池等效电路模型分析与比较的基础上,通过对动力锂离子电池进行多种特性实验,分析了锂离子电池的动态特性,提出了二阶RC等效电路模型,并验证了模型的准确性。在电路模型基础上运用扩展卡尔曼滤波算法搭建了MATLAB/Siumlink平台上的仿真模型,通过仿真和实验结果的对比,验证该模型具有较高的估算精度,可用于锂离子电池SOC的实时估算。
关键词:锂离子电池;等效电路模型; EKF算法; SOC估算
中图分类号:TM912.9文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.02.025
引用格式:凡旭国,周金治,高磊.锂离子电池特性建模与SOC估算算法的研究[J].微型机与应用,2017,36(2):83-86.
0引言
*基金项目:特殊环境机器人技术四川省重点实验室基金资助项目(13ZXTK07);西南科技大学研究生创新基金资助项目(16ycx100)可充放电锂离子电池自从20世纪90年代出现以来,由于具有体积小、质量轻、无记忆效应、无污染、可快速充放电等优势,已广泛应用于手机、笔记本电脑、数码相机等便携式电子产品[1]。电池使用时其荷电状态(SOC)的估算是电池管理系统(BSM)中的重要环节,准确地估算SOC能够提高电池的安全性能,有效地保护电池,延长电池的循环使用寿命,提高电池的使用效率[2]。
SOC估算算法的精确性直接依赖于用来描述电池特性的电路模型的准确性。常用的电池模型主要有三类[3]:电化学机理模型、神经网络模型和等效电路模型。由于电池内部化学反应复杂,很难在实际应用中建立精确的电化学机理模型;而神经网络模型则需要大量的历史数据来预测电池性能,并且模型只能针对特定因素分析,难以全面反映电池特性;等效电路模型能够考虑电压、电流、温度、极化等多种因素的影响,使用基本电路元件组成电路描述电池的工作特性,物理意义清晰明确,因而得到广泛应用。
目前国内外常用的等效电路模型包括:Rint模型、Thevenin模型、PNGV模型以及文献[4]提出的对PNGV模型改进的GNL模型等。文献[5]运用插值估算法结合PNGV模型对SOC进行了估算,有效地解决了安时法存在累计误差和初始值不准确的问题,最终使误差控制在5%以内;文献[6]将EKF算法用在一阶RC电路模型上,虽然取得一定的效果,但是考虑影响电池SOC的因素不够全面;文献[7]用神经网络和EKF相结合的方法实现了SOC的在线估计,但是依赖于电池大量的离线数据训练;文献[8]在等效电路模型的基础上将自适应滑模观测器运用于SOC的估算中,最后建立了仿真模型验证了方法的可行性,但算法误差和有效性不能得到保证。
本文通过对动力18650型锂离子电池进行多次充放电实验,分析了锂离子电池的动态特性,提出了二阶RC等效电路模型,并辨识了模型的相关参数,最后在MATLAB/Siumlink仿真平台上建立仿真模型,对模型进行仿真验证,通过仿真和实验结果的对比,验证该模型具有较高的估算精度。
1锂离子电池特性实验
1.1充电实验
锂离子电池常采用恒流转恒压的充电模式,本文以额定容量为2 600 mAh、充电电压4.3 V、标称充电电流0.25C~1C的18650型锂离子电池,实验平台为美诺M9710可编程电子负载和数控电源,通过实验可以获取其充电过程中电压电流的变化曲线,如图1所示。
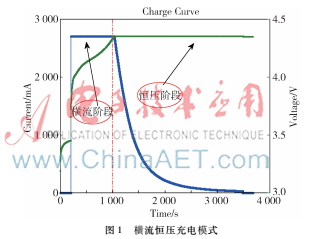
1.2放电实验
锂离子电池在不同的放电倍率下端电压响应不同,为获得电池在工作过程中端电压的变化,分别以0.3C、0.5C、1C放电倍率对电池进行恒流放电实验,得到各种倍率下电池的电压随时间变化的曲线如图2所示。

1.3复合脉冲实验
复合脉冲测试(Hybrid Pulse Power Characterization,HPPC)的目的是测试电池的动态特性,同时也可用来识别模型参数。首先进行10 s放电脉冲,经过40 s静置后再进行10 s充电脉冲,整个过程采用1C(即2.6 A)恒定电流充放电,并在HPPC循环测试中让电池等间隔SOC点进行复合脉冲实验,选取SOC为0.1,0.2,…,0.9,相邻脉冲实验之间的间隔为1 h(注:对于2 600 mAh电池容量,1C电流放电6 min,即放出260 mAh,SOC值下降0.1),电池静置1 h之后进入下一个HPPC循环。SOC为0.5时HPPC测试对应的电压响应曲线如图3所示。
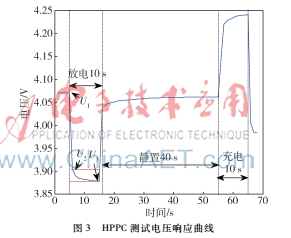
1.4OCV和SOC关系标定实验
开路电压(OCV)表征了电池在某一荷电状态下所对应的电动势,OCV与SOC具有一定的函数关系[9],实验分别采取0.3C、0.5C和1C的倍率放电,每放出0.1SOC时静置30 min,将记录到的电压值作为对应的开路电压,最终OCV和SOC的函数关系式通过对图4中三者的折中曲线进行多项式拟合得到。
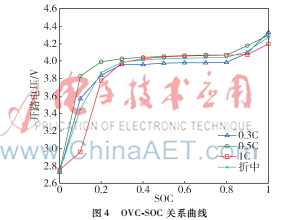
2等效电路模型及验证
由电池的特性试验可以得知无论是施加充电电流还是放电电流,其端电压都存在一个突变,之后又有一个缓慢变化的过程,因此可以用一个欧姆内阻和两个表征电池内部极化效应的RC环节来模拟电池的特性。等效电路模型如图5所示。

电池工作过程中模型的参数是动态变化的,因此模型中的五个参数需要进行参数的辨识。其中R0用电压突变阶段即式(1)得到,两个RC环节的参数用型如式(2)的二阶指数在MATLAB的cftool工具箱中采用拟合方式得到,
R0=U1-U2I (1)
f(x)=a*exp(-τ1*x)+c*exp(-τ2*x)(2)
式中τ1=RsCs、τ2=RlCl。
得到模型参数之后,在MATLAB/Simulink平台上建立二阶RC等效电路模型,设置仿真参数与自定义工况的实验数据做对比。图6为间歇横流放电下仿真电压与真实电压的对比,由图可见仿真值与真实值吻合较好,同时也验证了所建模型的准确性。

3EKF算法流程及实现
由于标准卡尔曼滤波算法只能用于线性系统,而扩展卡尔曼滤波算法(EKF)是通过将非线性系统的状态空间方程进行线性化处理,再利用卡尔曼滤波算法的递推过程对系统状态进行最优估算,因此本文采用EKF结合二阶RC模型的方法进行SOC的估算。
3.1EKF算法流程
EKF算法的非线性离散状态空间方程为[10]:
xk+1=f(xk,uk)+wk
yk=g(xk,uk)+vk(3)
式中,f(xk,uk)是非线性状态转移函数,g(xk,uk)是非线性测量函数。
首先,由基尔霍夫电压和电流定理得图5所示电路的时域方程如下:
i=CsdUsdt+UsRs
i=CldUldt+UlRl
Ubat=Uoc(SOC)-Us(t)-Ul(t)-R0i(4)
系统的状态量需要SOC,根据式(5)安时积分法的定义:
SOCt=SOC0-η∫t0idtQ(5)
选取SOC和两电容上的电压为状态量,对式(4)和式(5)进行离散化处理得到系统的更新方程如式(6)所示,测量方程如式(7)所示。
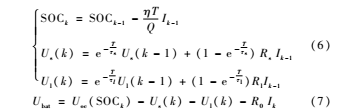
其次,令状态变量xk=[SOCkUs(k)Ul(k)]T,将式(6)、式(7)转化为矩阵形式:

最后,采用EKF算法的递推过程实现SOC的实时估算,具体步骤如下:
(1)初始化x0和P0。
(2)根据初值得到k时刻的状态向量的预测估计和均方误差的预测估计:

(3)计算卡尔曼滤波增益:
![]1Q8@ER2OFZ11_R2T5VWY2S.png ]1Q8@ER2OFZ11_R2T5VWY2S.png](http://files.chinaaet.com/images/2017/03/13/6362504132438392449429888.png)
(4)根据k时刻测量值和卡尔曼滤波增益Gk修正状态向量估计值,得到状态向量及均方误差的最优估计:
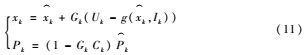
(5)返回步骤(2)进行下一轮估算,如此循环迭代就能得出每个时刻的SOC值。
3.2算法的实现
基于以上算法的分析,在MATLAB/Simulink平台上建立如图7所示的SOC估算仿真框图。该模型的输入为实际的电流,当前时刻的SOC估计值作为上一时刻的输入形成闭环系统,经过算法模块的迭代更新可在线得到每一时刻SOC的最优估计,将仿真结果与真实SOC比较来验证算法的鲁棒性。
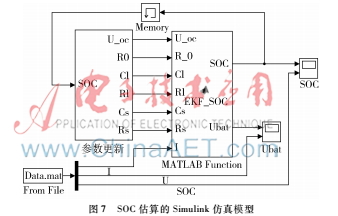
3.3算法的仿真验证
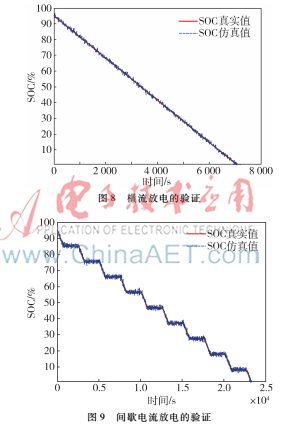
将实际实验测试的.mat数据输入模型中,设置好仿真时间,采样间隔取1 s,经过模型的递推估算可实时在线地得出每一时刻SOC的最优估计。
图8和图9分别显示了0.5C横流放电和间歇电流放电时真实的SOC和模型仿真出的SOC,结果表明,该算法估算出来的SOC值和真实值吻合度较好,并且无论是哪一种放电工况其误差都不超过5%。
4结论
本文通过充放电、HPPC实验以及开路电压实验建立了二阶RC等效电路模型来模拟电池的动态特性,并对模型进行了验证,针对锂离子电池工作过程中的非线性,提出了基于等效电路模型的扩展卡尔曼滤波算法并对算法的流程进行了分析,最后在MATLAB/Simulink平台上搭建了SOC估算的模型,验证了无论是横流还是间歇电流工况下该算法的误差都能控制在5%以内。
参考文献
[1] BESTER J E, EL H A, MABWE A M. Modelling of lithiumion battery and SOC estimation using simple and extended discrete Kalman Filters for Aircraft energy management[C].Industrial Electronics Society, IECON 201541st Annual Conference of the IEEE. IEEE, 2015: 2433-2438.
[2] ALVAREZ A J C, GARCIA N P J, de COS J F J, et al. Battery stateofcharge estimator using the MARS technique[J]. IEEE Transactions on Power Electronics, 2013,28(8):3798-3805.
[3] He Hongwen, Xiong Rui, Fan Jinxin. Evaluation of lithiumion battery equivalent circuit models for state of charge estimation by an experimental approach[J]. Energies, 2011,4(12):582-598.
[4] 林成涛,仇斌,陈全世.电流输入电动汽车电池等效电路模型的比较[J].机械工程学报,2005,41(12):7681.
[5] 杨阳,汤桃峰,秦大同,等.电动汽车锂电池PNGV等效电路模型与SOC估算方法[J].系统仿真学报, 2012,24(4):938-942.
[6] He Hongwen, Xiong Rui, Zhang Xiaowei, et al. Stateofcharge estimation of the lithiumion battery using an adaptive extended Kalman filter based on an improved Thevenin model[J]. IEEE Transactions on Vehicular Technology, 2011, 60(4): 1461-1469.
[7] CHARKHGARD M, FARROKHI M. Stateofcharge estimation for lithiumion batteries using neural networks and EKF[J]. IEEE Transactions on Industrial Electronics, 2010,57(12):4178-4187.
[8] Yin Chun, Zhong Qishui, Chen Yangquan, et al. Estimating the state of charge of lithium batteries based on fractionalorder slidingmode observer[C].Fractional Differentiation and Its Applications (ICFDA), IEEE, 2014: 1-6.
[9] WINDARKO N A, CHOI J. SOC estimation based on OCV for NiMH batteries using an improved takacs model[J]. Journal of Power Electronics, 2010,10(2):181-186.
[10] Yuan Shifei, Wu Hongjie, Yin Chengliang. State of charge estimation using the extended kalman filter for battery management systems based on the ARX battery model[J]. Energies, 2013,6(1):444-470.

