文献标识码: A
DOI:10.16157/j.issn.0258-7998.2017.02.021
中文引用格式: 王建新,李东旭,崔琦,等. FastICA在功耗分析去噪中的应用[J].电子技术应用,2017,43(2):88-91.
英文引用格式: Wang Jianxin,Li Dongxu,Cui Qi,et al. The application of the FastICA denoising in power analysis[J].Application of Electronic Technique,2017,43(2):88-91.
0 引言
功耗分析是一种利用密码设备运行时泄露的功耗信息进行密钥分析的方法。科研人员已经研究出许多种方式来应对噪声,LE T H[1]等提出四阶累积量来处理瞬时脉冲信号,能够有效减少高斯噪声。SOUISSI Y[2]等人提出采用卡尔曼滤波器的方法来减少高斯噪声。
但是传统的去噪方法具有一定的局限性,需要知道有用信号和噪声信号的特征。而应用独立成分分析技术,不需要知道有用信号和噪声具体分布,便能实现信号与噪声的分离,适用于在噪声频率不确定或者是存在同步加密噪声的情况下。
本文提出了将ICA技术应用于侧信道分析中,并用仿真加以实现,通过对比去噪前后的信噪比,证明了此种思路的正确性。
1 独立成分分析
1.1 发展概述
独立成分分析(Independent Component Analysis,ICA)技术属于盲信号分离技术(Blind Signal Separation,BSS)的一种[3]。1991年,HERAULT J和JUTTEN C[4]、SOROUCHYARI E[5]以及COMON P[6]在Signal Processing上发表了三篇关于盲信号分离的经典文章。1994年,COMON P首次提出了独立成分分析的概念。HYVIIRINEN A[7]等人提出了基于源信号非高斯性测度的快速固定点算法。
1.2 ICA理论介绍
ICA研究的问题是分析混合信号各组成成分,并使之统计依赖性最小,从而达到分离源信号的目的。本文用S(t)表示源信号矩阵,用X(t)表示混合信号,上述问题可以表示为:

衡量信号分离程度的独立性准则通常可以用非高斯度来进行衡量。本文基于快速固定点算法中,依据负熵最大化原则。
1.3 快速固定点算法(FastICA)理论介绍
1.3.1 负熵
FastICA算法用负熵来衡量非高斯性。负熵定义:

式中,Ng(Y)表示负熵,H(YGauss)表示高斯信号的熵,H(Y)表示信号熵。当负熵Ng(Y)的值越大,信号的非高斯性越大,分离程度越高。
1.3.2 FastICA的步骤
FastICA的基本步骤包括:(1)球化;(2)白化;(3)牛顿迭代法。由于迭代是在盲信号的情况下,无法计算熵值,可以使用近似公式:

通常情况下,对于超高斯信号,可以选择函数(7);对于亚高斯信号,选择函数(8)。
快速固定点算法的具体步骤:
(1)对待分离数据进行球化操作;
(2)对球化之后的数据进行白化操作,得到v;
(3)建立具有单位范数的初始化向量w;
(4)根据式(6),更新w,并进行矩阵标准化;
(5)判断收敛,收敛就得到一个独立分量,下一组数据执行步骤(2),如不收敛返回步骤(4);
(6)得到全部独立信号。
2 基于FastICA的功耗分析实验平台
2.1 侧信道平台的搭建
侧信道分析的平台架构图如图1所示。本文采用的加密算法为DES算法,采用的加密芯片为Mega16单片机最小系统板,采用的示波器是泰克公司的7104C数字存储示波器。
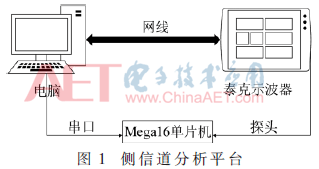
2.2 去噪流程
把采集到的加密算法的功耗信号与高斯噪声进行混叠,利用于负熵的快速固定点算法对混合信号进行区分,流程如图2所示。

3 基于FastICA的实验分析
3.1 功耗和噪声分离实验
首先进行了侧信道信息与高斯噪声和随机噪声的分离实验,分离过程中g函数选择的是公式(6)。将DES密码算法加密时单片机所泄露的功耗信息采集出来作为原始功耗信号,在MATLAB中将功耗信号与噪声进行混叠,再使用算法分离。原始信号分别为DES加密信号、随机噪声、高斯噪声,原始信号的曲线如图3所示。

通过基于负熵的快速固定点算法进行解混,分离信号如图4所示。

通过上面结果图可以看出,3组混合信号基本看不出DES加密的特征;而分离之后的3条曲线中,第二条能够明显看出DES加密的特征,另外两条曲线则是噪声。
3.2 两种加密算法功耗信号分离实验
本文做了两种加密算法的区分,使用的算法分别是DES和Present。此外,还混叠了一组高斯噪声信号。其原始信号和分离后的信号分别在图5、图6中显示。


3.3 计算信噪比
在前面的实验中,解混后信号无法与之前进行信噪比的衡量,于是,本文提出了如下的方法:
(1)将混合信号通过FastICA算法进行解混;
(2)将解混后信号矩阵中噪声行向量置零;
(3)将步骤(2)得到的矩阵经过FastICA反变换得到最终结果。
实验选DES加密信号与噪声的两通道混合曲线,经过上述方法后,最终得到的去噪前后对比如图7所示。
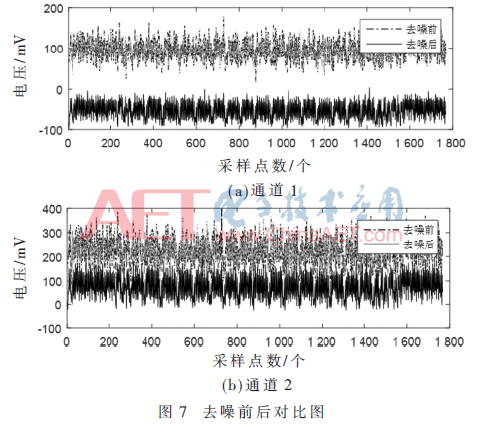
由图7可以看出,通过上述提出的方法,可以将ICA分离信号还原到固有的幅值,并计算去噪前后的信噪比,本文中应用的信噪比公式为:

式中,SNR表示信噪比,单位是dB;Psignal表示信号的能量;Pnoise表示噪声的能量。结果如表1所示。

3.4 比较不同g函数分离能力
在实验中将g函数由式(7)更新为式(8),并将其代入到式(6)中,进行DES加密信号与噪声的分离实验。实验结果如图8所示。
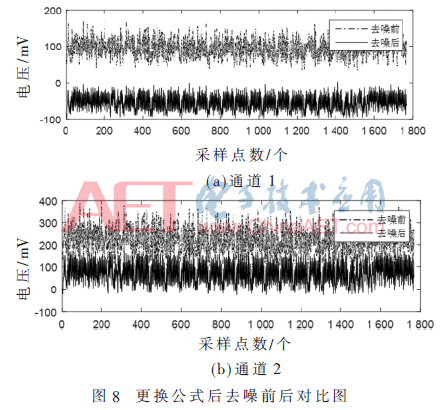
分别使用式(7)和式(8)对同一组数据进行实验,用信噪比的提升量和MATLAB中运算时间作比较,得到的对比结果如表2所示。

从表2可知,使用式(8)的分离效果要优于式(7)。为了追寻原因,本文引入峭度值对信号进行分析。峭度的公式如下:

式中kurt(x)表示峭度,如果值大于0,为超高斯信号;如果等于0,为高斯信号;如果小于0,为亚高斯信号。实验在MATLAB中应用峭度函数计算,得到DES加密信号峭度值为-0.812 7,证实其为亚高斯信号,而对于亚高斯信号,本文提到式(8)的分离能力相较式(7)更为出色。
4 结论
本文针对侧信道分析中存在的噪声问题,提出了一种用独立成分分析技术对采集到的功耗信息进行处理的方法。该方法能够有效地实现从混叠信号中区分出功耗信号和噪声,同时也能实现对不同加密算法的加密信号进行区分。提出了用ICA反变换的方式还原信号的幅值,计算出处理前后的信噪比,使用独立成分分析处理后的信噪比明显比去噪前的信噪比高,证明了此种方法确实可以应用到功耗分析去噪工作中。
参考文献
[1] LE T H,CLEDIERE J,SERVIERE C,et al.Noise reduction in side channel attack using fourth-order cumulant[J].Information Forensics and Security,IEEE Transactions on,2007,2(4):710-720.
[2] SOUISSI Y,GUILLEY S,DANGER J,et al.Improvement of power analysis attacks using Kalman filter[C].Acoustics Speech and Signal Processing(ICASSP),2010 IEEE International Conference on.IEEE,2010:1778-1781.
[3] LEE W T.Independent component analysis:theory and applications[Book Review].IEEE Transactions on Neural Networks,1999,10(4):982.
[4] HERAULT J,JUTTEN C.Space or time adaptive signal processing by neural network models[J].Neural networks for computing.AIP Publishing,1986,151(1):206-211.
[5] SOROUCHYARI E.Blind separation of sources,Part III:Stability analysis[J].Signal Processing,1991,24(1):21-29.
[6] COMON P,JUTTEN C,HERAULT J.Blind separation of sources,Part II:Problems statement[J].Signal Processing,1991,24(1):11-20.
[7] HYVIIRINEN A,KARHUNEN J,OJA E.Independent component analysis[M].New York:Wiley and Sons,2001.
作者信息:
王建新,李东旭,崔 琦,肖超恩,陶勇勇
(北京电子科技学院 电子与通信工程系,北京100070)

