0 引言

    相关向量机(Relevance Vector Machine，RVM)^[1]是建立在支持向量机(Support Vector Machine，SVM)基础上的一种学习方法，依靠稀疏贝叶斯统计理论建立训练模型。RVM与SVM相比，函数形式相似，但RVM的核函数不需要满足Mercer条件以及能提供概率式输出使它更具优势^[2]。近年来RVM在回归估计、模式识别及工程领域方面^[3]得到了较为广泛的应用，但仍存在最优核参数不易确定的问题，所以部分学者将智能优化算法应用到RVM核参数寻优中^[4]，取得了一定的成效。

    果蝇算法^[5](Fruit fly Optimization Algorithm，FOA)是由PAN W T根据果蝇觅食的行为提出的一种智能优化算法。虽然该算法被广泛应用到各个领域^[6]，但在实际应用过程中，也存在陷入局部最优解的情况，文献[7]提出了具有Levy飞行特征的双子群果蝇优化算法（LFOA），有效地解决了FOA陷入局部最优的问题，提高了算法的性能。为了提高RVM分类器的性能，本文提出了一种基于LFOA算法的RVM核函数参数优化方法，并通过UCI标准数据库的仿真实验，验证了方法的有效性和可靠性。

1 相关向量机

1.1 模型描述

    假设每个样本独立分布，p(t|x)采用Bernoulli分布，可得预测结果t的后验概率的似然函数为：

    根据概率预测公式，新的输入向量x?鄢所对应的目标向量t?鄢求得的条件概率为：

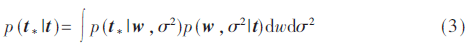
    根据稀疏Bayes理论，给权值向量w分配独立的零均值Gauss先验分布：

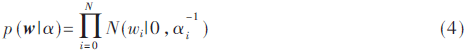
    经过多次迭代后可发现大部分权值都变得很小，只有很少一部分权值非零，根据式(1)，只有非零权值对应的训练向量对目标值起作用，称为相关向量(RVs)，则RVM模型可重新表示为：

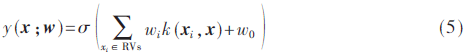
1.2 RVM多分类

    最后，通过式(8)累加所有分类器的概率输出，并采用“最大概率赢^[9]”的策略将x_test判定为累加后验概率最大的类别。

1.3 核参数对RVM分类性能的影响

    相关向量机的核函数可将低维数据样本映射到高维特征空间，从而实现样本的线性可分，所以其参数的设置对RVM的分类性能有着极其重要的影响。研究以比较常用、非线性映射能力较强的径向基核函数^[10](RBF Kernel)为例，利用UCI数据库中Sonar分类数据（共208个样本）进行试验，将Sonar数据集中的全部数据作为训练样本对RVM分类模型进行训练，同时也将全部数据作为测试样本输入已训练的RVM模型中进行学习能力测试。核参数值与相关向量(RVs)和训练时间的关系如表1所示。

    根据表1可知，随着核函数参数逐渐增大，相关向量的数量呈现逐渐下降的趋势，不同核参数所对应的训练时间不同，为进一步说明核函数参数对RVM性能的影响，图1给出了分类准确率随着核参数的变化趋势。

    由图1和表1可知，改变核函数参数实际上是改变映射函数关系，进而改变数据样本映射到高维特征空间的可区分程度，所以核参数的选取对RVM性能有较大程度的影响，同时也只有选择适当的核参数，RVM的学习能力和泛化能力才能得到提升。

2 LFOA-RVM核参数优化方法

2.1 LFOA算法

    LFOA算法是将Levy飞行特征和果蝇算法相结合，利用Levy飞行的高度随机性使果蝇种群容易跳出局部最优，LFOA算法的具体步骤参见文献[7]。

    LFOA算法在寻优过程中，分别计算果蝇个体与当代最优个体和最差个体的欧式距离Dist_best和Dist_worst，若Dist_best<Dist_worst，则将果蝇个体划分到较优子群，否则划分为较差子群，迭代过程中，两个子群的果蝇个体数量是动态变化的。较优子群围绕最优个体按式(9)进行Levy飞行：

2.2 LFOA-RVM优化核参数流程

    基于LFOA算法优化RVM核参数的流程如图2所示，具体步骤如下：

    (1)将数据集分为训练样本和测试样本，训练样本用于RVM核参数选择和建立RVM分类模型，测试样本则用于检验RVM分类器性能；

    (2)初始化LFOA算法种群规模、迭代次数、果蝇个体起始位置和搜索距离以及Levy飞行步进长度等参数；

    (3)对训练样本采用5折交叉验证[11](5-fold cross validation)，将交叉验证平均准确率作为适应度函数，选择最大准确率对应的核参数值作为RVM分类模型参数的设定值；

    (4)根据果蝇个体的适应度，按照与最优个体和最差个体间的欧氏距离大小将果蝇分类，并按式(9)和式(10)进行位置更新；

    (5)计算新位置果蝇的适应度，按照规则更新全局信息；

    (6)重复步骤(4)和(5)，最终输出最优核参数值。

3 仿真实验 

3.1 数据源与参数设置

    为了验证LFOA-RVM的有效性，从UCI机器学习标准数据库中选取了4个数据集进行仿真实验。算法采用MATLAB R2011b实现，RVM工具箱为SB2_Release_200^[12]，实验中使用的UCI数据集如表2所示。

    为了便于对比，分别利用LFOA、FOA、遗传算法(GA)和粒子群算法(PSO)同时对RVM的核参数进行寻优。将全部算法的种群规模设置为20，最大迭代次数为100，g的搜索范围设置为0~500；在LFOA算法中步进长度设置为1.5；GA算法中，交叉概率p_c=0.7，变异概率p_m=0.1；PSO算法中局部搜索参数c₁=1.5，全局搜索参数c₂=1.7。

3.2 结果分析

    利用表2中的4组数据按照2.2节所述的优化流程对LFOA-RVM性能进行测试，寻优迭代过程中的适应度曲线如图3所示。

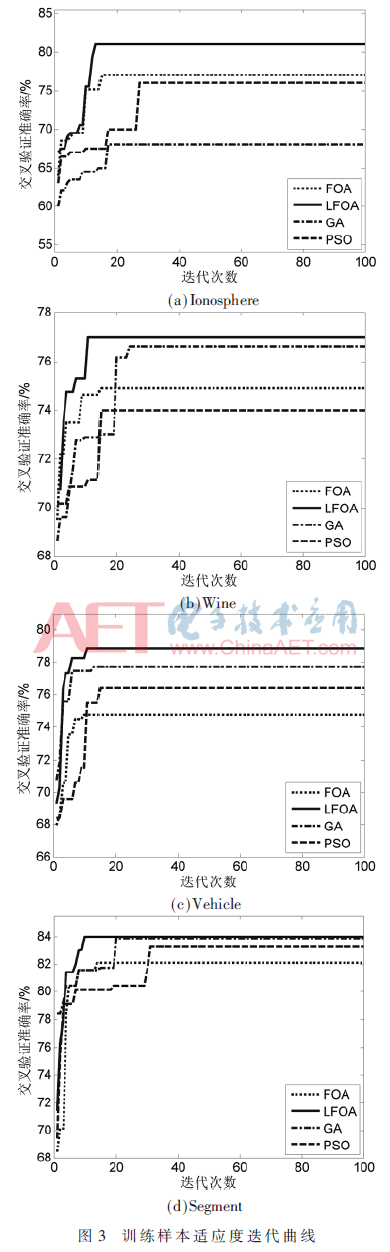
    根据图3可知，FOA、GA和PSO算法在寻优时都不同程度的出现了陷入局部最优解而无法跳出的情况，与以上3种算法相比，LFOA由于Levy飞行高度的随机性从而更容易跳出局部最优，并且适应度更高，寻优速度更快。

    4组数据集测试样本的测试结果如表3~6所示。在表3~6中，平均准确率为使用数据集进行5次实验后得到的平均测试准确率；最高准确率为实验过程中得到的最高测试准确率；最优核参数为达到最高测试准确率时RVM分类模型核函数参数的值。

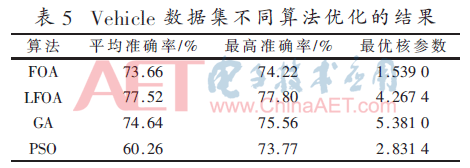
    根据测试结果可知，LFOA-RVM不论是解决二分类问题或者是多分类问题，都可以达到较高的测试准确率，并且4组UCI数据集的最优核参数值跨度较大，表明了LFOA算法具备较强的全局搜索能力，验证了利用LFOA算法进行RVM核参数寻优的有效性。为了便于比较各算法的寻优稳定性，计算出多次实验的测试结果方差，如表7所示。

    由表7可知，Ionosphere、Wine和Segment数据集进行多次测试，LFOA算法所得的方差小于其他几种算法，Vehicle数据集中LFOA测试结果的方差虽略大于FOA，但明显小于其他两种算法，表明了LFOA-RVM测试结果的波动程度较小，验证了该方法具有较高的寻优稳定性；LFOA结合了FOA算法局部寻优精度高与Levy飞行容易跳出局部最优值的优势，提高了全局搜索能力，所以与FOA、GA和PSO 3种算法相比，LFOA算法搜索精度更高，性能更稳定。综合以上分析可知，LFOA算法可较精确地搜索RVM的最优核参数，并能达到较高的测试准确率，较其他几种算法而言，具备一定优势。

4 结论

    RVM核函数参数的选取对其分类性能有着显著的影响。针对这一问题，本文采用LFOA算法对RVM核参数进行寻优，通过几个典型的UCI数据集进行测试，得出该算法可较精确地搜索到RVM的最优核参数，具备较强的局部寻优精度和全局搜索能力，有效地提高了RVM分类模型的性能。相比于传统的果蝇算法、遗传算法和粒子群算法具有更高的寻优精度和稳定性，为选取最优RVM核函数参数提供了一种新方法、新途径。

参考文献

[1] TIPPING M E.Sparse Bayesian learning and the relevance vector machine[J].Journal of Machine Learning Research，2001，1(3)：211-244.

[2] 范庚，马登武，张继军，等.基于决策树和相关向量机的智能故障诊断方法[J].计算机工程与应用，2013，49(14)：267-270.

[3] 张旭峰，杨丰瑞，郑建宏.基于RVM的可重用性SoC测试平台设计[J].电子技术应用，2006，32(5)：82-84.

[4] 陈景柱.布谷鸟优化混合核相关向量机的网络流量预测[J].计算机与现代化，2015(5)：94-97.

[5] PAN W T.A new fruit fly optimization algorithm：Taking the financial distress model as an example[J].Knowledge-Based Systems，2012，26(Complete)：69-74.

[6] 刘翠玲，张路路，王进旗，等.基于FOA-GRNN油井计量原油含水率的预测[J].计算机仿真，2012，29(11)：243-246.

[7] 张前图，房立清，赵玉龙.具有Levy飞行特征的双子群果蝇优化算法[J].计算机应用，2015，35(5)：1348-1352.

[8] 任学平，庞震，辛向志，等.基于小波包最优熵与RVM的滚动轴承故障诊断方法[J].轴承，2014(11)：48-53.

[9] 周勇，何创新.基于独立特征选择与相关向量机的变载荷轴承故障诊断[J].振动与冲击，2012，31(3)：157-161.

[10] 姚全珠，蔡婕.基于PSO的LS-SVM特征选择与参数优化算法[J].计算机工程与应用，2010，46(1)：134-136.

[11] 姚畅，陈后金，YANG Y Y，等.基于自适应核学习相关向量机的乳腺X线图像微钙化点簇处理方法研究[J].物理学报，2013，62(8)：1-11.

[12] TIPPING M E.An efficient MATLAB implementation of the sparse Bayesian modelling algorithm[CP/OL].(2009-03-12)[2016-05-10].http：//www.Relevancevector.com.

作者信息:

吕  岩，房立清，赵玉龙，张前图

（军械工程学院 火炮工程系，河北 石家庄050003）