庞战1,2，滕奇志1，何海波2

　　（1. 四川大学 电子信息学院图像信息研究所，四川 成都 610064；2. 成都西图科技有限公司，四川 成都 610064）

       摘要：为了解决传统的基于尺度不变特征变换（SIFT）算法的图像拼接方法无法使用SIFT特征匹配算法对岩石薄片图像中的空白区域图像进行特征提取，进而影响整个岩石薄片图像拼接的问题，在尺度不变特征变换匹配算法的基础上，提出了一种将岩石薄片图像的行列中心位置作为拼接基准点的图像拼接方法。该方法改进了特征点的提取方式、变换矩阵的计算顺序以及矩阵优化的顺序，并利用相邻图像之间的位置关系估计出空白区域图像的变换矩阵，实现了整个岩石薄片图像的拼接。实验结果表明，该方法可以较好地完成岩石薄片图像中空白图像的拼接，能够较为完整地保留整个岩石薄片的纹理信息，具有一定的实际应用价值。

　　关键词：尺度不变特征变换；空白区域；岩石薄片；估计；图像拼接

　　中图分类号：TP391.4文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.06.015

　　引用格式：庞战，滕奇志，何海波. 基于SIFT的岩石薄片图像拼接［J］.微型机与应用，2017,36（6）：46-50.

0引言

　　*基金项目：国家自然科学基金项目（61372174）图像拼接是指将在同一环境或者条件下拍摄的一组相互之间具有一定重合量的图像，通过提取特征点、图像配准等处理后，得到一幅包含岩石薄片中各个图像纹理信息的全景图。目前，图像拼接技术在很多方面都有广泛的应用价值［1］。

　　在石油地质分析中，由于显微镜视域的限制，无法一次性采集得到宽视域岩石薄片的全景图［2］。为了从整体上分析岩石薄片，只能先对岩石薄片分区域采集得到整个薄片的图像，然后将图像拼接成一幅大视域图像。目前，图像拼接主要采用SIFT算法，通过图像预处理、图像配准以及融合完成图像拼接［35］ 。SIFT算法主要应用在相邻的具有明显特征点和一定重叠量的图片拼接中。然而，由于岩石薄片的不规则性，岩石薄片通常包括空白区域(如图1所示)，由于无法进行特征提取，导致整个岩石薄片图像的拼接失败。

　　本文在SIFT算法的基础上，通过改变SIFT特征提取的顺序与方式、配准的基准点位置和变换矩阵的计算以及优化方式，实现整个岩石薄片图像的拼接。实验结果表明，该方法能够得到比较完整并且包含了各个图像信息的岩石薄片全景图。

1相关理论

　　1.1SIFT算法的基本原理

　　SIFT算法是由哥伦比亚大学的LOWE D G教授于1999年提出，并在2004年完善的［6］。该算法的具体流程如下：

　　（1）构建尺度空间，检测极值点

　　尺度空间是模拟图像数据的多尺度特征，检测图像中具有尺度不变性的位置。1994年，LINDEBERG T发现唯一有可能的尺度空间内核是高斯函数［7］。假设I(x,y)表示一幅图像，尺度可变的高斯函数用G(x,y,σ)表示，则其尺度空间的定义如式（1）所示。

　　L(x，y,σ)=G(x,y,σ)*I(x,y)（1）

　　其中，σ代表尺度因子，其大小表示平滑程度，*为卷积运算符，高斯函数的定义用式（2）表示：

　　G(x,y,σ)=12πσ2exp(－(x2+y2)/2σ2)（2）

　　LOWE D G使用高斯差分算子(DoG)主要有两个原因：一是能够更方便地检测出稳定的关键点；二是考虑到计算的复杂程度。

　　D(x,y,σ)=(G(x,y,kσ)－G(x,y,σ))*I(x,y)

　　=L(x,y,kσ)－L(x,y,σ)（3）

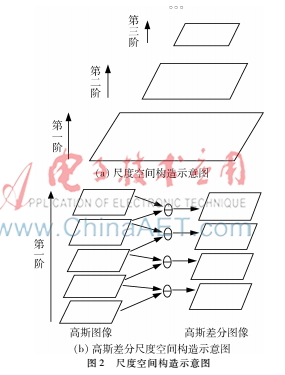
　　其中，k为阈值。LOWE D G在实验中，通过对原始图像进行降采样构造若干阶尺度空间，如图2（a）所示，然后在每一阶尺度空间内利用高斯函数卷积得到若干层高斯图像，再差分生成高斯差分尺度空间，如图2（b）所示。在同一个尺度内，将每一个像素点同时与该像素点同尺度的8个相邻点以及上下两个相邻尺度对应的18个像素点的值进行比较，只有当该像素点的值是最大或者最小值时，才称该像素点是图像在该尺度下的一个特征点，也叫关键点。最后，对其余的每一阶尺度空间都重复以上操作，直到检测完所有尺度空间中的关键点为止。

　　（2）定位关键点，去除不稳定点

　　LOWE D G使用拟合三维二次函数的方法准确定位检测出来的关键点的位置和尺度。该方法可以有效去除对比度低以及稳定性较差的关键点。使用的尺度空间函数的泰勒公式展开式如式（4）所示：

　　其中，X=(x,y,σ)T，在采样点处，计算D和D的导数，当其导数为零时，得到极值点的X1，如式（5）所示：

　　利用尺度空间函数在极值点处的函数值去除对比度较低的响应点。将式（5）代入式（4），计算得到极值点处函数值，如式（6）。

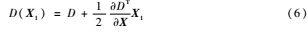
　　通常情况下，若|D(X1)|≥0.03，该特征点就保留，否则就去除。

　　因为高斯差分算子在边缘处会产生比较强烈的边缘响应，在该算子中，差的极值点在边缘处具有较大的曲率，在垂直方向上具有较小的曲率。因此，可以利用该性质去除边缘响应。主曲率可以通过一个2×2的Hessian矩阵H求出，如式（7）所示。

　　D的主曲率和H的特征值成正比，若假设α为最大特征值，β为最小特征值，则矩阵H主对角线的值和行列式的值用式（8）和式（9）表示。

　　如果曲率大于式（10）结果的比值，则舍弃。LOWE D G在实验中通过对比发现，当r=10时，能够最大程度去除不稳定的边缘响应点［6］。

　　（3）确定关键点的大小和方向

　　在初步确定了关键点的位置之后，可以利用图像的局部特性为每一个关键点分配一个基准点，使该关键点的特征描述符具有旋转不变性。对于高斯金字塔检测出来的关键点，使用其高斯金字塔邻域窗口内像素的梯度特征和方向特征对描述符进行描述。(x,y)处的梯度值m(x,y)和方向θ(x,y)的表达式如式（11）和式（12）所示。

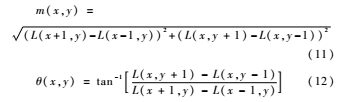
　　其中，L所用的尺度为每个关键点各自所在的尺度。为了进一步准确给出关键点的方向，一般采用梯度直方图统计的方法，以关键点为中心的邻域窗口内的像素的梯度和方向。直方图峰值所代表的方向即为关键点的方向。通过上述各个步骤之后，检测出的包含位置、所在尺度以及方向的关键点称为图像的特征点。

　　（4）生成特征描述子

　　为了确保关键点不受光线等因素的影响，可以为每一个关键点建立一个描述子，使其具有独特性，进而可以提高特征点的匹配率。为了保证描述子具有旋转不变性，首先将方向旋转到关键点的方向。LOWE D G的实验中，在关键点所在的尺度空间中，以关键点为中心，选取一个8×8的窗口，然后在每个4×4的窗口内计算8个方向的梯度方向直方图，绘制每个梯度方向的累加可形成一个种子点，最终获得一个4×4×8共128维的向量特征。

　　（5）特征点的匹配

　　SIFT特征向量生成后，一般使用最近邻域算法对特征点进行匹配。利用特征点的最短欧氏距离和次最短欧氏距离的比值与所设定的阈值的大小关系作为判断两个特征点是否为一匹配对的依据。如果结果小于阈值，则认为这一对特征点是匹配的。LOWE D G在实验中发现，将阈值设定为0.8比较合适，在计算特征点的欧氏距离之后，可以先利用BBF（BestBinFirst）算法对特征向量进行快速处理，再使用RANSAC算法去除误匹配的特征点［7］。

　　1.2变换矩阵计算的基本原理

　　描述图像之间位置关系的矩阵称为变换矩阵。图像的变换矩阵可以通过特征匹配对计算得到［89］。在同一个空间下，两幅图之间的变换关系用式（13）表示，其中，(x1,y1)为参考图像上的点，(x2,y2)为目标图像上与(x1,y1)对应的点，M称为变换矩阵:

　　在式（13）中，线性方程组中有8个未知变量，则至少需要4对特征点匹配对才能求解方程组的解。整理并将结果进行向量化用式（14）表示:

　　A1=MA2（14）

　　若矩阵A2AT2可逆，则可以求解得到变换矩阵M，如式（15）所示：

　　M=(A1AT2)(A2AT2)-1（15）

　　只要有足够多可用的特征点匹配对就可以通过式（15）计算得到图像之间的变换矩阵，从而确定图像之间的相对位置关系。

2空白区域图像拼接方法

　　岩石薄片中空白区域的图像（见图1）虽然可以使用SIFT算法对相邻图片进行特征匹配，但由于空白区域图像的表面特征比较单一，纹理信息不丰富，检测到的特征点匹配对大多都是错误匹配，在使用RANSAC算法［10］去除错误匹配之后，可用的特征匹配数目很少。如图3所示，从实验对比结果可以看出，岩石薄片中空白区域的相邻图像的特征匹配数目在使用RANSAC算法去除错误匹配之后，没有可用的特征点匹配对，无法利用式（15）求出图像的变换矩阵，从而无法确定两张图片的相对位置，影响整个岩石薄片图像的拼接。

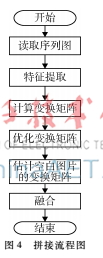
　　图4拼接流程图在实际应用中，为了解决该问题，在SIFT算法的基础上，提出了一种选取岩石薄片图像的中心位置为基准点的拼接方法。并利用空白区域图像与其相邻图像之间的位置关系估计出空白区域图像的变换矩阵，实现了整个岩石薄片的拼接。流程图如图4所示。

　　2.1特征点提取

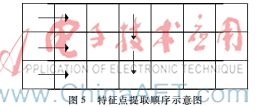
　　为了解决SIFT算法无法提取空白区域图像的特征点的问题，本文在SIFT算法的基础上，改变了特征点提取的方式，并在RANSAC算法筛选时设定阈值，如筛选结果小于阈值则视为不能正常匹配，并标记。本实验设定的阈值为30，该阈值也可以根据图片特征点的具体情况进行设定。如图5所示，该示意图表示3行7列图片。其中，横向箭头表示每一行图片的特征点提取顺序，竖向箭头表示中间一列图片的特征点提取顺序。具体步骤如下：

　　（1）获取待拼接岩石薄片图像的行和列的数目。

　　（2）分别对岩石薄片图像中的每一行和中间列进行特征提取，并对不能正常匹配的图片进行标记。

　　2.2计算变换矩阵

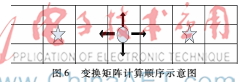
　　由于无法得到空白区域图片的特征点匹配对，从而无法确定空白区域图片的相对位置。在前文特征提取顺序的基础上，对变换矩阵的计算顺序作了相应的调整。如图6所示，其中每一格代表一张图片，圆形代表本文选取的中心位置，五角星代表空白图片，箭头表示变换矩阵的计算方向，每一行图片变换矩阵的计算方向都与示意图中箭头表示的方向一致。文中，“左（右）侧”是表示分别对左侧和右侧都进行相同的操作。具体步骤如下：

　　（1）选取岩石薄片图像的中心位置（图6中圆形所在位置），并初始化其变换矩阵为单位矩阵，作为变换矩阵计算的基准点。

　　（2）从中心位置所在行开始，到图像的起始行，分别从每一行的中间位置开始，对左（右）侧的图片计算变换矩阵，如果遇到标记图像（图6中圆形左（右）侧五角星代表的图片）则停止计算当前图片的变换矩阵，并对标记图片左（右）侧的所有图片的变换矩阵赋值为空。

　　（3）从中心位置所在行开始到图像的最后一行，分别从每一行的中间位置开始重复步骤（2）。

　　（4）从图像中间列的中间位置开始，对中间列图像的上下两部分的图片重复步骤（1）和（2）。

　　2.3优化变换矩阵

　　计算完所有图片的变换矩阵之后，本文在上一节提出的变换矩阵的计算顺序的基础上，对变换矩阵的优化方式作了相应的调整。具体优化方式如下：

　　（1）从中心位置所在行开始到图像的起始行，分别从每一行的中间位置左（右）侧的图片进行变换矩阵优化，如果遇到标记图像则停止优化。直至每一行图像都重复该操作为止。

　　（2）从中心位置所在行开始到图像的最后一行，分别从每一行的中间位置开始重复步骤（1）。

　　（3）从薄片图像中间列的中间位置开始，对中间列图像的上下两部分的图片重复步骤（1）和（2）。

　　2.4估计空白区域图片的变换矩阵

　　变换矩阵优化完成之后，为了获得完整的拼接结果，需要估计空白区域图片的变换矩阵。具体方法如下。

　　（1）从中心位置所在行开始到图像的起始行，分别从每一行的中间位置开始，对其左（右）侧的图片进行标志位扫描，遇到标记图片，则利用该标记图片右（左）侧相邻两张图片的变换矩阵与标记图像之间的相对位置关系估计出标记图片的变换矩阵，同时位于标记图片左（右）侧的所有图片的变换矩阵均通过该方法依次得到。直至每一行图像都重复该操作为止。

　　（2）从中心位置所在行开始到图像的最后一行，分别从每一行的中间位置开始重复步骤（1）。

　　（3）从图像中间列的中间位置开始，对中间列图像的上下两部分的图片则重复步骤（1）和（2）。

　　完成上述处理之后，通过相应的融合算法对结果图进行融合，消除拼接缝［11］，完成整个岩石薄片图像的拼接。

3实验对比结果及分析

　　本文使用6行6列共36张图片进行实验，图片尺寸都是5 184×3 456，实验所用的图像包含了实验所需要的薄片信息。实验结果如图7~9所示，其中，图7是实验所用的图像，图8是基于SIFT算法的拼接结果图，图9是本文提出的拼接方法的结果图。

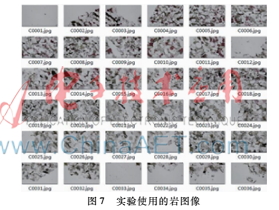
　　从实验的对比结果中可以明显看出，当采集得到的岩石薄片图像中包含空白区域图片时，如图7实验使用的图像中“C0001.jpg”和“C0033.jpg”等图片，因为无法使用SIFT算法对岩石薄片中空白区域图片完成配准，因此，只能在拼接前剔除这些图片所在的行或者列的所有图片，对比可以看到基于SIFT算法的拼接结果图中，第一张图片所在的列和下方最后一行都存在严重缺失（结果图中的黑色缺失部分）。而本文提出的图像拼接方法则较为完整地完成了整个岩石薄片图像的拼接，较好地反映出整个岩石薄片中颗粒的分布情况，保证了岩石薄片的完整性。因此，本文提出的图像拼接方法能较好地完成岩石薄片空白区域图像的拼接，能较为完整地展示岩石薄片的全貌，具有一定的实际应用价值。

4结论

　　本文首先介绍了SIFT算法和变换矩阵计算的基本原理，同时对岩石薄片中空白区域图像不能使用SIFT算法进行特征点提取的原因作了简要分析，并在此基础上分别对本文提出的图像拼接方法中的特征点的提取方式、变换矩阵的计算方式、变换矩阵的优化方式以及估计空白区域图片的变换矩阵的具体步骤进行了描述，在不改变岩石薄片整体性基础上，完成了包含空白区域的岩石薄片图像的拼接，保证了岩石薄片纹理信息的完整性。本文的不足之处在于，若在高倍显微镜下岩石薄片的中心区域存在大量空白区域，则无法具体确定拼接的基准位置，对该方法的使用具有一定的限制。

　　参考文献

　　［1］ 徐鑫, 孙韶媛, 沙钰杰，等. 一种基于RANSAC的红外图像拼接方法［J］. 激光与光电子学进展，2014，51(11):129-134.

　　［2］ 岳永娟, 苗立刚, 彭思龙. 大规模显微图像拼接算法［J］. 计算机应用，2006, 5(26):1012-1014.

　　［3］ 邹承明, 侯小碧, 马静. 基于几何学图像配准的SIFT图像拼接算法［J］. 华中科技大学学报（自然科学版），2016，44(4)：32-36.

　　［4］ 汪松, 王俊平, 万国挺，等. 基于SIFT算法的图像匹配方法［J］. 吉林大学学报（工学版），2013，43(S1):279-282.

　　［5］ 白廷柱, 侯喜报. 基于SIFT算子的图像匹配算法研究［J］. 北京理工大学学报，2013，33(6):622-627.

　　［6］ LOWE D G. Distinctive image features from scaleinvariant keypoints［J］. International Journal of Computer Vision，2004，60(2): 91110.

　　［7］ LINDEBERG T. Scalespace theory: a basic tool for analyzing structures at different scales ［J］. Journal of Applied Statistics, 1994, 21(2):225-270.

　　［8］ 郭红玉, 王鉴. 一种基于RANSAC基本矩阵估计的图像匹配方法［J］. 红外，2008，29（2）: 5-8.

　　［9］ 曲天伟, 安波, 陈桂兰. 改进的RANSAC算法在图像配准中的应用［J］. 计算机应用，2010，30（7）：1849-1851.

　　［10］ FISCHER M A, BOLLES R C. Random sample consensus: a paradigm for model fitting with applications to analysis and automated cartography ［J］. Communication of the ACM,1981, 24 (6):381-395．

　　［11］ 苗启广, 王宝树. 基于改进的拉普拉斯金字塔变换的图像融合方法［J］.光学学报，2007，9(27): 1605-1610.