孙璐,马震
(滨州学院 信息工程系,山东 滨州 256600)
摘要:外部输入通过神经元群模型可以产生不同类型的类似EEG的信号,但是外部输入信号的统计特性多采用经验值,而没有对其专门进行研究。在设定神经元群模型参数的情况下,SR-UKF被用来估计不同观测值所对应外部输入以及模型输出。实验证明外部输入估计数据的均值在前人所采用值的范围内,但是标准差比前面用到的小很多。
关键词:EEG信号;神经元群模型;集合系数模型;均方根不敏卡尔曼滤波器;拟合
中图分类号:TP181文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.06.016
引用格式:孙璐,马震. 基于SRUKF的神经元群模型分析[J].微型机与应用,2017,36(6):51-52,61.
0引言
*基金项目:山东自然科学基金项目 (ZR2014FL005);滨州学院科研基金项目(BZXYG1004, BZXYG1007)脑是一个通过生物电来处理信息的综合神经系统。作为一种间接体现脑行为的手段,脑电图(EEG)能反映大量神经细胞记录在大脑头皮表面或大脑皮层的一系列生物电活动[12]。
EEG信号的复杂性反映了产生它的复杂的皮层结构。为了研究皮层结构,很多数学模型被开发来模拟脑电行为。参考文献[3]、[4]给出了基于神经生理学的皮层柱模型,并对模型的细节进行了探索。
从生理学的角度来看,JANSEN B H的神经群模型是将神经元群分为了相互作用的子群,子群直接通过兴奋的或者抑制的突触相互连接,突触的数量决定了子群间相互作用的强度。本文采用均方根不敏卡尔曼滤波器(Square Root Unscented Kalman Filter, SRUKF)对JANSEN B H的模型的输入进行估计,并对估计结果进行了分析。
1Jansen神经元群模型
神经元群模型结构如图1所示,图1中阴影部分为椎体神经元,无阴影部分为中间神经元。
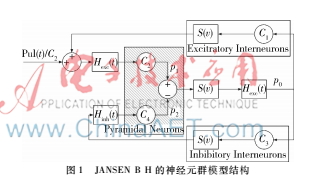
线性变换的冲击响应分别为Hexc(t)和Hinh(t),它们将来到神经元群的动作电位的平均脉冲密度变换到后突触膜平均电位,该电位可以是兴奋的或者抑制的。Hexc(t)和Hinh(t)的表达式具有以下形式:

非线性环节S(v)将一个神经元群的平均膜电位变换为动作电位的平均脉冲密度,这个变换用如下形式的Sigmoid函数来描述:
S(v)=2e0/(1+er(v0-v))(2)
椎体细胞与兴奋、抑制中间神经元间的相互作用通过四个连接常数C1~C4来表示,与神经元的轴突(axons)和树突(dendrites)之上的中间神经元建立的突触总数成正比。
2基于SR-UKF的神经群输入估计

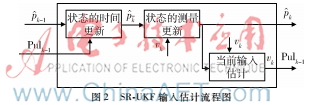
SR-UKF通过一组精确选择的sigma点来匹配随机量的统计特性,可以保证经过非线性系统后,估计量的统计特性与真实值偏差较小。SR-UKF[5]因其无需进行Jacobian矩阵的计算及对非线性系统进行近似,并且其运算量与线性化方法也在同一数量级,从而成为解决非线性参数、状态估计问题的常用方法。JANSEN B H的神经元群模型输入估计的流程如图2所示。首先通过对状态向量进行时间更新和测量更新而获得当前时刻的状态估计值。由于当前时刻的外部输入来自于神经元群外部,因此不能通过神经元的状态方程更新,但是可以在已知观测值的情况下通过解卷积得到。计算得的状态矢量和外部输入值又用于下一次的估计。具体的步骤如下:
(1)初始化状态的均值,并通过Cholesky分解计算状态协方差矩阵的均方根:
0=E[p0],S0=chol{E[(p0-0)(p0-0)T]}
其中状态都初始化为0,经过解卷积,Pul0=aexcy0/Aexc。
(2)计算(2N+1)个σ点,σ0,k=0,σi,k(i=1,2,…,2N)分别取±Sk的一行,χi,k-1=k-1+σi,k。
(3)时间更新;
(4)测量更新;
(5)当前输入估计。通过对状态矢量的更新,可以根据当前的观测值,通过解卷积的方式求得当前输入的估计值,并可以用于下一次的状态更新。
3实验结果
所采用的脑电数据来自于德国波恩癫痫研究室的数据库的F和S集[6]。每个集包含100个单通道脑电数据,每段数据的长度为23.6 s,采样率为173.6 Hz。这些数据采用目测检查的方法,去除了伪迹、干扰,并经过裁剪而得到。其中F集记录了没有癫痫发作的脑电记录,而S集记录了癫痫活动。从F集和S集各随机选择10段数据,并经过重新采样,使数据的采样率转换为256 Hz。采用上面所述的SR-UKF方法对所选数据进行拟合。在拟合之前,采用Runge-Kutta-Fehlberg算法解微分方程,并得到离散时间序列。
表1给出了外部输入估计值的统计数据,它们的均值分布在198~202之间,平均值为200.74。外部输入估计数据的标准差分布在0.12~4.53之间,其中发作数据估计值的分布区间要大于不发作数据估计值的分布区间。其中,数据12、14、15、18的方差不足1,而数据11和19的方差都超过4。
4结论
JANSEN B H的模型中采用在120~320均匀分布的信号来建模外部输入信号,能产生与EEG信号类似的信号。Wendling等人所提出的模型中采用均值为90、标准差为30的高斯噪声来建模外部输入信号,通过确定三个模型参数,可以使频域与原始信号较好地匹配。Ponten等人用神经群模型对结构性和功能性连接之间的关系进行了分析,所采用的外部输入为标准差为0.1的高斯白噪声。而本文的实验数据显示,外部输入估计数据的平均值为200.74,其标准差分布在0.12和4.53之间。可见,估计数据的平均值与JANSEN B H的模型的外部输入相吻合,而标准差却与他人所采用的都不相同。而上述不同分布的输入信号在实验中都表现出较好的性能,所以可以简单地推断,在神经元群模型中,外部输入信号对模型输出的作用要小于模型参数,可以将对神经元群模型的研究重点放在其结构和参数上。
参考文献
[1] AWADA K A,JACKSON D E,WILLIAMS J T,et al. Computational aspects of finite element modeling in EEG source localization[J]. IEEE Engineering in Medicine and Biology Society,1997,44(8):736-752.
[2] Zhang Yingchun, Ding Lei, van DRONGELEN W, et al. A cortical Potential imaging study from simultaneous extra and intracranial electrical recordings by means of the finite element method[J]. Neuroimage, 2006,31(4):1513-1524.

