文献标识码: A
DOI:10.16157/j.issn.0258-7998.2017.03.026
中文引用格式: 王思拨,马社祥,孟鑫,等. 基于训练序列的OFDM频率同步改进算法[J].电子技术应用,2017,43(3):104-107.
英文引用格式: Wang Sibo,Ma Shexiang,Meng Xin,et al. Improved frequency synchronization method for OFDM systems based on training sequence[J].Application of Electronic Technique,2017,43(3):104-107.
0 引言
2013年5月,在国际电信联盟无线电通信工作组(ITU-R Working Party 5B)会议上,多国政府和国际航标协会(IALA)提出了VDES(VHF Data Exchange System)。VDES是针对AIS加强和升级的系统,由AIS(Automatic Identification System)、ASM(Application Specific Messages)以及VDE(VHF Data Exchange) 所组成的集成系统。VDES允许多于一种编码速率和调制方式,可以在系统规模和业务可用性上提供更多的灵活性。VDE采用自适应调制和编码来使频谱效率和吞吐量最大。2015年10月,国际电信联盟无线电通信第5研究组建议VDES采用ITU-RM.2092-0建议书[1]。在VDE-SAT上/下行链路50 kHz专用信道中,可以采用OFDM技术。在VDES中的VDE-SAT上/下行链路通信时,卫星通信的环境给OFDM技术的使用造成了同步问题。
OFDM同步技术主要是对OFDM系统中符号定时偏差(Symbol Timing Offset,STO)和载波频率偏差(Carrier Frequency Offset,CFO)进行估计,同步方法可分为两类:(1)非数据辅助方法[2],主要是利用循环前缀(Cyclic Prefix,CP)的盲估计算法;(2)数据辅助的估计方法[3-7]。数据辅助类算法中最经典的是由SCHMIDL M等人[2]提出的同步算法(以下简称S&C算法),但循环前缀导致这种算法存在定时平台,造成定时模糊现象。MINN H及PARK B等人[4,5]对S&C算法进行了改进,虽然有效地防止了定时估计的峰值平台问题,但是在纠正小数倍载波偏差时误差较大,且要求训练序列的偶数位是等比数列,这样才能纠正整数倍载波偏差,算法复杂度高[8,9]。文献[6]中虽然利用CAZAC(恒包络零自相关)序列设计的训练符号可以准确定时,但在定时同步时都使用了本地序列,存在计算量大的缺点,并且载波频偏估计的性能没有得到改进。Guo Yi等人在文献[7]中提出使用实训练序列,利用时域训练序列的共轭特性,准确定时。但是在对小数倍频偏估计时,由于训练序列中没有重复结构,只能用基于循环前缀的ML算法进行估计,估计范围较小,低信噪比下估计性能较差,整数倍频偏估计算法复杂。本文利用Guo Yi的符号定时方法准确定时后,对频率同步算法改进,根据时域训练序列结构的共轭对称性,利用新的度量函数求出小数倍频偏;根据接收端频域训练序列的循环移位估计整数倍频偏。本文频率同步改进算法在不降低估计精度的前提下扩大了小数倍频偏估计的范围,提高了整数倍频偏的正确检测概率。
1 OFDM系统模型
定义发送信号为x(n),接收信号为y(n),带有循环前缀的发送端信号可以表示为:

2 训练序列结构的设计
在发送端,在频域设计新的训练序列,偶数位发送:

奇数位发送:


在接收端,时域接收信号可以表示为:

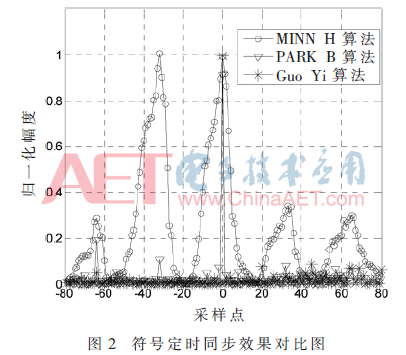
可根据式(12)估计出准确符号定时位置,如图2所示。估计出符号定时偏差后,对信号进行补偿,实现符号定时同步。
3 改进的频偏估计算法
经符号同步算法估计出符号起始点,在时域上进行小数倍载波频偏估计;补偿后,将信号从时域变换至频域,在频域进行整数倍载波频偏估计。
3.1小数倍载波频偏估计
在接收端准确定时后,在时域上对小数倍频偏估计,时域接收信号可以表示为:



3.2 整数倍载波频偏估计
当频偏ε只存在小数倍频偏时,可用上述方法准确估计;当频偏中存在整数倍频偏时,经过小数倍频偏估计且补偿后,接收信号中仅存在偶数倍频偏[3]。在接收端补偿小数倍频偏后,只存在整数倍频偏εi,且εi为偶数,时域接收信号可以表示为: 利用FFT对接收信号解调后,Y(k)=X(k-εi),Y(k)为X(k)的循环移位,得到Y(k)的偶数位序列:
利用FFT对接收信号解调后,Y(k)=X(k-εi),Y(k)为X(k)的循环移位,得到Y(k)的偶数位序列:
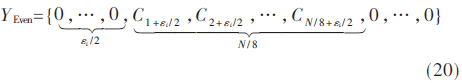
通过求解码后的训练序列能量值最大处,定位原偶数位训练序列的非零训练序列起始位置,该位置的移位个数即为估计的整数倍频偏:

4 仿真结果及分析
在理论分析的基础上进行仿真实验,对本文算法的性能进行测试。在仿真过程OFDM系统的主要参数为:FFT/IFFT的变换长度为128,循环前缀长度为32,子载波采用16QAM调制方式,仿真次数为100次。
图4为各算法在不同的CFO下MSE的性能对比。如图4(a)所示,当ε=0.3时,本文算法MSE性能优于MINN H算法和PARK B算法,在较低信噪比下Guo Yi算法MSE性能明显降低,而本文能保持良好的MSE性能。在图4(b)中,当ε=2.3时,实际频偏值超出了MINN H算法和PARK B算法的估计范围, MINN H算法和PARK B算法不能用于频偏估计,本文算法比Guo Yi算法有更好的估计性能。

图5中比较了本文算法与Guo Yi算法的整数倍频偏估计性能。从图5中可以看出,本文算法在信噪比较低时整数倍频偏正确检测的概率较高,具有更好的同步性能。



5 结论
本文在符号定时准确的基础上,对OFDM系统的载波频率偏差进行估计,提出了一种基于新型训练序列结构的OFDM频率同步的改进算法。根据接收端的时域接收信号中存在部分共轭特性进行小数倍频偏估计,在频域根据训练符号的移位估计出整数倍的频偏。理论推导和仿真结果都表明,本文算法扩大了小数倍频偏的估计范围,小数倍频偏估计在低信噪比下有更好的MSE性能,提高了整数倍频偏的正确检测概率,具有很好的估计性能。
参考文献
[1] International Telecommunication Union.Technical characteristics for a VHF data exchange system in the VHF maritime mobile band[S].Recommendation ITU-RM.2092-0,October 2015.
[2] VAN DE BEEK J J,SANDELL M,BRJESSON P O.ML estimation of timing and frequency offset in OFDM systems[J].IEEE Trans on.Signal Processing,1997,45(7):1800-1805.
[3] SCHMIDL T M,COX D C.Robust frequency and timing synchronization for OFDM[J].IEEE Trans.Commun.,1997,45(12):1613-1621.
[4] MINN H,ZENG M,BHARGAVA V K.On timing offset estimation for OFDM systems[J].IEEE Commun.Lett.2000,4(7):242-244.
[5] PARK B,CHOEN H,KO E,et al.A novel timing estimation method for OFDM systems[J].IEEE Commun.Lett.,2003,7(5):53-55.
[6] 严春林,李少谦,唐友喜,等.利用CAZAC序列的OFDM频率同步方法[J].电子与信息学报,2006,28(1):139-142.
[7] Guo Yi,Liu Gang,Ge Jianhua.A novel time and frequency synchronization scheme for OFDM systems[J].IEEE Trans on Consumer Electronics,2008,54(2):321-325.
[8] CHO Y S,KIM J,YANG W Y,et al.MIMO-OFDM wireless communication with MATLAB[M].1st ed.John Wiley and Sons(Asia) PteLtd,2010.
[9] NISHAD P K,SINGH P.Carrier frequency offset estimation in OFDM Systems[C].Proceedings of 2013 IEEE Conference on Information and Communication Technonlogies(ICT2013),2013:885-889.
作者信息:
王思拨,马社祥,孟 鑫,王俊峰
(天津理工大学 计算机与通信工程学院,天津300384)

