0 引言

    甲状腺结节一直以来都是一个非常普遍的医学问题，研究表明全球大约有50%的人都有甲状腺结节^[1]。因此对甲状腺结节的病理特征研究就显得特别重要，而在此之前对结节所在区域进行精确的分割就成为了当前的首要任务。图像分割在数字图像处理领域中处于很重要的地位，国内外学者对此作了广泛研究。文献[2]提出的CV(Chan Vese)模型就是一种常用的分割模型。该模型利用图像全局信息能有效克服斑点噪声和干扰，并且能很好地处理模糊边缘，抗噪性强，但对灰度不均匀的图像分割效果差；MUMFORD D^[3]等人对该算法进行改进提出了PS(Piecewise Smooth)模型。虽然该模型克服了CV模型的缺点，但计算量过大；Li Chunming^[4]等人在CV模型的基础上提出了LBF(Local Binary Fitting)模型。该模型引入高斯函数构造两个图像的局部拟合函数，能有效获取图像的局部灰度信息，并用它们替代CV模型中两个全局拟合函数，实现了对大部分灰度不均匀图像的分割，但由于其在演化过程中多次使用卷积，因此计算量大，而且必须选择合适的初始轮廓位置才能获得精确的分割结果； ZHANG K H^[5]等人在LBF模型的基础上提出了LIF(Local Image Fitting)模型，该模型对灰度不均匀图像分割时不仅能取得较理想的分割效果，而且与LBF模型相比迭代次数明显降低，因此分割效率大大提高。但LIF模型仅在分割效率和参量设置上作了改进，对初始轮廓的选取依旧敏感。

    文献[6]指出，图像的灰度值不能简单地用一种分布来描述，不同点的灰度均匀性不同，因此仅用一个固定的模型来计算不同区域的灰度统计信息是不准确的。因此，本文提出了一种新的水平集活动轮廓模型来分割甲状腺结节图像。首先在经典的LIF模型中加入局部梯度信息，构造了既包含有灰度信息也包含有梯度信息的GLIF(Gradient Local Image Fitting)模型，并以此构造局部拟合能量项。然后再用经典的CV模型构造全局能量函数。最后将两种能量结合起来，使得水平集函数在局部能量和全局能量的共同支配下朝着目标的真实边界演化。 实验结果表明，本文模型不仅能准确分割具有低对比度、弱边缘、强噪声、灰度不均匀等特点的图像，而且对初始轮廓的敏感性也有所降低。

1 相关模型描述

1.1 CV模型

    CHAN T F和VESE L提出的CV模型^[2]，其基本思想是把图像分为背景区域和目标区域两部分，并且假设这两个部分的灰度值都各自是均匀的。对于图像区域内任一闭合曲线C，c₁和c₂分别用来表示曲线C内部和外部的灰度均值，则CV模型能量泛函的水平集形式如下所示：

    CV模型较传统的活动轮廓模型有了较大的改进，它无需计算图像梯度，并且综合利用了图像的全局信息，因此对大部分的图像都能实现准确的分割。但对灰度不均匀图像，例如甲状腺结节超声图像，该算法无法对其进行精确的分割。

1.2 LIF模型

    ZHANG K H^[5]等人利用图像的局部灰度统计信息来构造图像局部拟合函数，从而提出了LIF模型。对于图像中任一点x∈Ω，LIF模型的能量泛函定义为如下形式：

其中，m₁、m₂表示的是由高斯窗函数决定的局部灰度均值。LIF模型虽然可以实现对灰度不均匀图像的分割，但其对初始轮廓位置的选取比较苛刻，只有当初始轮廓位置选取合适时才能取得精确的分割结果。

2 本文提出的模型

2.1 改进的LIF模型

    传统的LIF模型仅单一地利用图像的局部灰度信息来分割灰度不均匀图像，当图像受噪声污染严重时可能无法获得令人满意的分割结果，且演化时水平集函数极易面临局部最优。而引入图像的梯度信息可以去除图像上相当部分的局部极小值和噪声，因此对传统的LIF模型进行改进，引入图像的局部梯度信息，利用两种局部统计信息构造新的局部能量拟合模型称之为GLIF模型。该新模型由于多用了一个局部梯度信息，可以更好地约束水平集能量泛函的收敛，因此也就在很大程度上避免了传统LIF模型容易出现局部极小的问题。对于任一点，(x∈Ω)该新模型的水平集形式能量泛函表示如下：

    GLIF模型利用图像局部灰度统计信息和局部梯度信息克服了演化过程中易陷入局部极小值的缺点，但其对初始轮廓的位置依然比较敏感。为了解决这一问题，本文提出了结合CV模型全局性优点的方法。

2.2 融合全局与局部的CV-GLIF模型

    考虑到甲状腺结节超声图像往往呈现明显的灰度不均匀，而且结节区域边界通常比较模糊，所以单单利用GLIF模型或CV模型都不可能完成对结节区域的精确分割。为了实现对甲状腺结节的有效分割，提出了GLIF模型和CV模型相结合的算法，集成了两种模型各自的优点。其能量泛函的水平集形式表示如下：

    式(13)中等号右边第一项表示的是全局能量项，由CV模型的全局项构成；第二项表示的是局部能量项，由GLIF模型构成。从而使得水平集函数在局部能量与全局能量的共同控制下向着目标区域的真实边界演化。β∈[0，1]是一个常数，全局能量项与局部能量项所占比重都由其支配。对于β的选取要依据图像灰度的不均匀程度而定，当分割灰度严重不均匀的图像时，局部能量起支配作用，所以此时要选择较小的β；而当分割灰度比较均匀的图像时，全局能量起支配作用，所以此时就要选择较大的β。式(13)的隐式偏微分方程如下：

3 实验结果

3.1 甲状腺结节分割实验结果

    经实验测得该模型的时间步长Δt=0.001，λ₁=1.0，λ₂=2.4。实验平台是Windows 7旗舰版, PC处理器为intel(R)core(TM)i3-2020cpu@3.30GHz，内存是4 GB，软件版本为MATLAB2012b(64 bit)。

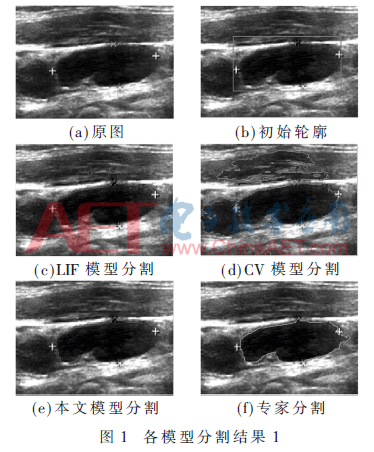
    图1(a)的整体灰度不均匀，结节局部边缘模糊。从实验结果看出，只有本文方法可以准确地找到结节区域的边界。而LIF模型陷入了局部极小值，CV模型则出现了过分割。

    在图2中，结节与背景区域对比度很低，结节区域边缘模糊。只有本文模型可以准确地分割出结节区域，而CV模型与LIF模型都出现了错误分割。

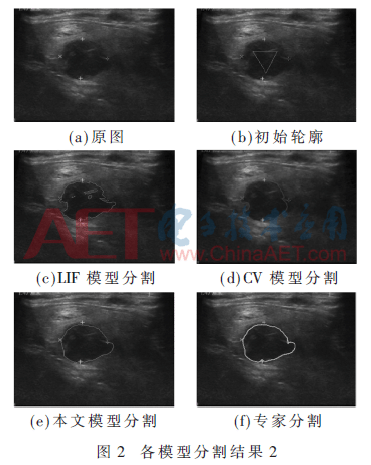
    图3是一幅被噪声严重污染的图片。从实验结果看，只有本文方法可以准确分割出结节。LIF模型因为噪声的干扰而导致错误分割。CV模型法的全局拟合项，针对该类图像很难准确定位到边缘，因此出现过分割现象。

3.2 CV-GLIF模型初始轮廓位置实验

    为了验证本文提出的模型对初始轮廓位置的敏感性程度，与LIF模型进行了对比实验，结果如图4所示。

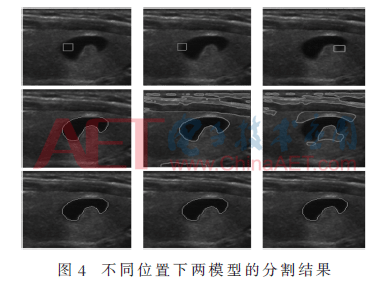
    图4中，第一行表示的是所选取的3个初始轮廓的位置，第二行表示的是LIF模型对应于3个位置时的分割结果，第三行表示是用本文方法进行分割时对应于3个不同位置的分割结果。从实验结果可以看出，采用LIF模型分割时，只有当初始轮廓的位置完全位于结节区域内时才能得到较精确的分割结果。而本文提出的模型在上述3种位置时都能实现较精确的分割。

3.3 实验结果分析

    为了确定实验中各个模型的分割精度，本文采用SHATTUCK D W^[7]等提出的骰子相似系数法(Dice Similarity Coefficient，DSC)来计算各个模型对应的分割精度，DSC的值越接近于1则表示分割的精度越高。图1～图3图像的DSC值见表1。

DSC的表达式为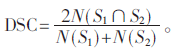其中S₁是由专家手动给出的目标区域的分割图像；S₂是由上述模型分割出的目标区域；N(S)表示的是对应区域的面积，用该区域中像素的数目来表示。

4 结论

    本文采用了以CV模型为全局能量、以改进的LIF模型为局部能量相结合的水平集方法实现了甲状腺结节超声图像的分割。 综合考虑了CV和GLIF两种模型各自的优点，构造了能有效分割灰度不均匀图像的新模型。最后将本文算法的分割结果与LIF模型和CV模型的分割结果进行对比。实验结果表明，本文算法克服了LIF模型与CV模型的缺点，不仅分割精度高，而且能有效抑制噪声的干扰。

参考文献

[1] HERMUS A R，HUYSMANS D A.Treatment of Benign nodular thyroid disease[J].The new England Journal of Medicine，1998，338(20)：1438-1447.

[2] CHAN T F，VESE L.Active contours without edges[J].IEEE Transactions on Image Processing，2001，10(2)：266-277.

[3] MUMFORD D，SHAH J.Optimal approximation by piecewise smooth functions and associated variational problems[J].Communications on Pure & Applied Mathematics，1989，42(5)：577-685.

[4] Li Chunming，Kao Chiu-Yen，GORE J C，et al.Implicit active contours driver by local binary fitting energy[C].IEEE Conference on Computer Vision and Pattern Recognition，2007：1-7.

[5] ZHANG K H，SONG H，ZHANG L.Actives contours driven by local image fitting energy[J].Pattern Recognition，2010，43(4)：1199-1206.

[6] 刘驰，孙权森.一种新的结合图像梯度的局部活动轮廓模型[J].计算机应用研究，2014，31(11)：3510-3513.

[7] SHATTUCK D W，SANDOR-LEAHY S R，SCHAPER K A，et al.Magnetic resonance image tissue classification using a paaial volume model[J].Neuroimage，2001，13(5)：856-876.

作者信息:

王  昕，李  亮

（长春工业大学 计算机科学与工程学院，吉林 长春130012）