0 引言

    随着现代集成电路工艺的发展，单位面积上所能集成的晶体管数量不断增加，时钟频率不断提升，限制应用实现性能提升的主要因素将不再是硬件资源，而是如何充分利用这些资源^[1]。粗粒度可重构分组密码阵列（Coarse-Grained Reconfigurable Block Encryption Array，RBEA）提供了大量密码运算资源，是针对分组密码算法高速实现而设计的加速平台。在该平台上通过设计分组密码算法SM4的不同映射方案，来探究提高运算性能和资源效率的最佳方法。

1 SM4算法简介

    SM4算法是2012年3月国家密码管理局授权的分组密码算法^[2]。该算法主要由32轮迭代组成，每轮迭代完全相同，均为非线性运算，运算数据位宽有8 bit和32 bit两种。SM4算法的数据分组长度为128 bit，密钥长度也为128 bit。

    轮运算的主体是F函数，该函数的运算位宽为32 bit，每轮更新32 bit数据，其表达式如式(1)所示。

    第32轮运算结束后将运算结果进行交换得到最终的密文。

2 粗粒度可重构密码阵列

    RBEA是针对分组密码算法开发的粗粒度可重构运算平台。可重构设计采用数据流驱动，通过可重构单元的配置来满足不同密码算法的需求，具有高效率和高并行度的特点^[3]。粗粒度单元的设计不同于传统的细粒度可重构单元，在实现分组密码算法时速度更快、效率更高^[4]。

2.1 阵列结构

    RBEA的基本结构如图1所示，由输入输出控制器、共享存储区和运算阵列组成。

    FB中的4种运算单元FU1-4是在文献[4]中有所描述。对分组密码算法操作分析分类的基础上，通过整合三输入布尔函数、移位、模加减、模乘、比特置换、S盒运算和有限域乘法等7种基本操作而设计形成的异构单元。分组密码算法中常用的非线性操作SBOX通过共享存储与FB联合实现。在功能单元（简称FU）输出端增加异或单元，主要用于完成指定运算操作后结果与其他数据进行后异或运算。

    运算阵列使用分散-聚簇设计方案，一行中相邻的4个FB中的FU通过固定连线共同完成64 bit和128 bit的运算。该阵列固定输入输出结点，由输入控制器负责数据注入和运算启动，输出控制器负责数据输出。配置单元提供的配置信息将FB重构为需要的运算功能和数据路径，共享存储在本地控制器控制下完成运算存储操作。

2.2 算法映射过程

    不同于传统以指令流驱动的处理器平台，阵列平台在实现算法映射时，通过运算、路由和存储单元的重构配置来完成数据流的实现，通过控制单元配置来完成控制流的实现^[1]。映射基本流程如下：

    （1）数据流配置

    使用图形化编程工具搭建算法任务中的数据路径，主要包括运算结点、寄存结点和结点连接等，并将这些任务分配到1个或多个FB上。最后通过布局布线算法完成阵列结构上的数据路径搭建。

    （2）控制流配置

    通过设置周期级参数，在不同时刻产生所需的控制信号。使用汇编语言对输入输出与FB中的控制器进行编程，完成数据输入输出和运算控制任务。

    （3）阵列配置信息生成

    通过集成的编译器将配置好的数据路径和控制参数信息编译成阵列配置信息，完成算法映射。

3 SM4算法的不同映射方案

    通过对SM4算法的研究，结合RBEA的结构特点，本文采用操作合并、循环展开和任务并行复制等策略设计了不同的算法映射方案，并对这些方案进行评估来探究提高性能和资源效率的最佳映射策略。

    通过对SM4算法的分析，仅需要移位、异或和S盒3种操作就可以完成全部运算。移位操作通过配置移位单元可以实现，异或操作通过配置三输入布尔函数单元或直接使用各FU输出端口的异或单元实现，S盒操作由配置共享存储器实现。运算过程中的以32 bit为单位的数据移位可以直接通过路由实现，不占用功能单元资源。

    使用吞吐率和性能面积比来量化地比较不同方案的性能和资源效率情况[5]。式(4)为吞吐率公式，表示单个时钟内的平均数据处理量，单位为bit/cycle。式(5)为性能面积比公式，表示平均每个FB上单个时钟内的平均数据处理量，单位为bit/cycle perFB。

    其中S为处理分组个数，C为分组大小，T为数据运算所需时钟数，N为映射方案中FB的个数。

3.1 操作合并

    将各步骤操作独立的映射到各个FB上，如图2所示。由于数据输入端口的限制，轮运算共需9个FB，6个时钟周期完成。由于最后的交换可以通过路由单元进行交换，不占用运算资源和时间。因此完成1组数据加密共占用9个FB，(6×32)+3=195个时钟周期，其吞吐率为0.65 bit/cycle，性能面积比为0.07 bit/cycle perFB。

    这种映射方案，对于每个FB来说，只利用到了其中的1种FU，而对于其他FU完全没有利用，FB的利用率仅为25%。通过分析发现，轮密钥异或可以与S盒操作合并，而线性变换L的操作也可以合并，其合并后的映射结构如图3所示。合并方案中轮运算只占用6个FB，4个时钟周期，完成1组数据的加密时，N=6，T=131，性能为0.98 bit/cycle，提高了1.5倍，性能面积比为0.16 bit/cycle perFB，提高了2.25倍，效果非常明显。

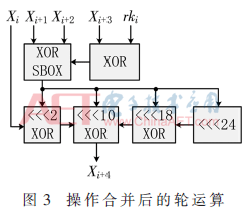
    由于阵列结构中单元的独立性允许将算法映射到更多的单元上进行并行运算，因此操作合并方案减少了资源占用，提高了性能，为其他并行方案打下了基础。

3.2 任务并行

    为提高SM4算法的性能，需要使用大量单元来承担计算任务。本文认为使用这些单元的方式无非是将运算任务分配到这些单元上，并利用阵列特点，使这些单元能够并行运算。分配方式主要有两种，一种是不同的单元组合独立地承担不同数据的运算任务，即基于数据分配的任务复制方案；另一种是使不同的单元组合分别承担同一数据运算的不同阶段的计算任务，即基于循环展开的流水方案。

    任务复制方案在合并操作的基础上，将各个算法任务完整复制到未利用的单元上。由于输入输出的限制，只能将任务复制为4份，如图4所示，4个阴影部分表示为4份复制后的任务。

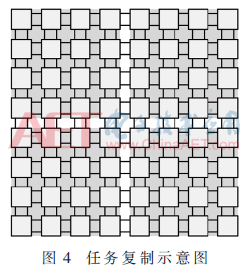
    在当前的映射方案中，理想情况下，性能提升4倍，但资源利用率是原始方案的37.5%，性能面积比仅为0.06 bit/cycle perFB，还不如操作合并前的资源利用率。因此，采用任务复制的方案关键在于如何能够保证资源利用率不被显著地降低，这样才能最大化地提高性能。

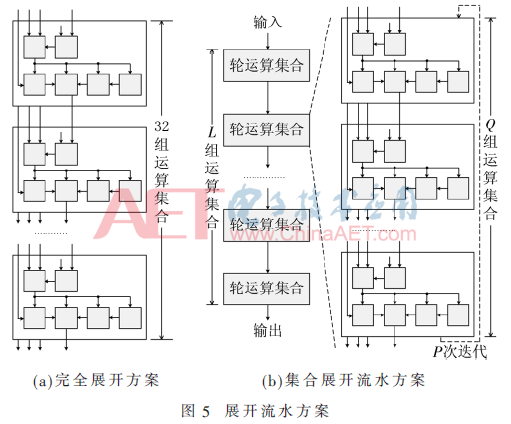
    循环展开流水方案在合并操作的基础上，将轮运算进行复制映射，不同的轮运算承担不同迭代次序的运算，被映射的单元接力处理数据，共同完成对一组数据的加/解密运算。针对阵列提供的资源不同，其流水形式也有所不同，可以分为全展开流水和集合展开流水。全展开流水以合并操作后的轮运算为基本单位进行复制映射，复制次数与迭代次数相同，如图5(a)。集合展开流水同样以轮运算为基本单元，而复制次数则根据外部条件设定，每个轮运算映射的单元不再承担单次迭代任务而是多个轮运算任务的集合，如图5(b)所示。集合展开方案需要满足L×P×Q≥32。可以看出，全展开方案是集合展开在P=0，Q=1设定情况下的特殊形式。

    根据流水线工作原理，吞吐率计算公式为：

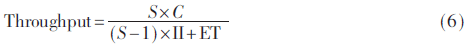
    其中II为迭代间隔，ET为处理一组数据所用的时钟周期数。

    在全展开方案中，II=4，ET=131，N=192，其吞吐率极限值为32 bit/cycle，性能面积比最大为0.167 bit/cycle perFB。性能提升明显，而资源利用效率与操作合并方案基本相同。

    在集合展开方案中，为达到最小II，应使Q=1，P=4，为简化布线，映射时直接认为每轮运算占用两行共8个FB。共占用48个FB，II=16，ET=131，其吞吐率极限值为8 bit/cycle，性能面积比最大为0.125 bit/cycle perFB。相对于操作合并后的方案，其性能提高了约7.8倍，而资源利用效率却下降了，这是因为这种映射方案中共有16个FB未使用。为了提高资源利用效率需要研究自动布局布线算法，能够将未使用的FB充分使用起来。

4 实验验证与分析

    在65 nm工艺下，RBEA的工作频率为320 MHz，测试数据量大小分别为1 KB、16 KB、32 KB、48 KB、64 KB，不同方案的测试结果如表1所示。

    对比操作合并前后的实验数据可以看出，SM4算法实现性能有较大提升，而且性能面积比提升效果非常明显。采用任务复制的方案能够线性地提升算法性能，但是由于阵列结构的限制，其资源利用率却有所降低。采用循环展开流水方案能够显著地提升算法实现性能，但是同样地其性能面积比有所下降。

    对于与SM4结构相似的算法，采用合并操作能够实现提升性能和资源利用率的双重效果，而任务复制和循环展开方案仅能够提高性能却对资源利用的提升没有贡献。究其原因，是由于SM4算法实现的轮运算完全相同，一轮运算硬件可以实现完整算法映射，该组硬件在迭代运算过程中，始终处理被占用状态，即以该组硬件为模板进行复制设计其他方案时资源利用率不会提高。因此，基于合并操作的后续方案中不能够超越这一方案。若想进一步提升资源效率，应该进一步降低II，增加流水深度。

5 结论

    基于操作合并和任务并行这两种思路，本文在RBEA平台上对SM4算法设计了不同的映射方案，并通过实验数据分析了不同方案对性能和资源效率提升的影响。实验结果表明，合并操作减少了操作时间和资源，显著地提升了算法实现性能和资源效率；任务并行使用更多资源来提升性能，但没有提升硬件资源使用效率。通过增加流水深度、减少迭代间隔和使用自动化布局布线算法，将会进一步提升算法的在该平台上的实现性能和资源使用效率。

参考文献

[1] 魏少军，刘雷波，尹首一.可重构计算处理器技术[J].中国科学：信息科学，2012(12)：1559-1576.

[2] 国家密码管理局.国家密码管理局公告第23号[EB/OL].GM/T 0002-2012.(2012-03-21).http：//www.oscca.gov.cn/News/201204/News_1227.htm.

[3] 杨子煜，严明，王大伟，等.面向CGRA循环流水映射的数据并行优化[J].计算机学报，2013，36(6)：1280-1289.

[4] Li Wei，Zeng Xiaoyang，Nan Longmei，et al.A reconfigurable block cryptographic processor based on VLIW architecture[J].China Communications，2016，13(1)：91-99.

[5] LIU B，BAAS B M.Parallel AES encryption engines for many-core processor arrays[J].Computers IEEE Transactions on，2013，62(3)：536-547.

[6] SIM H，LEE H，SEO S，et al.Mapping imperfect loops to coarse-grained reconfigurable architectures[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2016，35(7)：1092-1104.

[7] SHAO S，YIN S，LIU L，et al.Map-reduce inspired loop parallelization on CGRA[C]//IEEE International Symposium on Circuits and Systems.2014：1231-1234.

[8] ZHOU L，LIU H，ZHANG J.Loop acceleration by cluster-based CGRA[J].Ieice Electron Express，2013，10(16).

[9] 朱敏，刘雷波，尹首一，等.面向对称密码领域的可重构阵列设计[J].微电子学，2012，42(6)：815-818.

作者信息:

徐金甫，杨宇航

（信息工程大学，河南 郑州450000）