0 引言

    集成电路和信息技术的日益发展，支付宝、淘宝、网银以及微信等互联网应用的迅速普及，为人们日常生活、学习和工作带来极大便利。大量的信息共享带来方便的同时，也出现信息泄露与被篡改的威胁，如网上银行账户被盗、个人隐私泄露以及棱镜门事件等。因此如何保证数据信息的安全在密码学中显得尤为突出。Hash函数又称哈希函数或者杂凑函数，是现代密码学中最基本的模块之一，以任意长度的消息值作为输入，生成固定长度的输出数据。Hash函数在数字签名、文件校验、鉴权协议以及流密钥产生、伪随机序列生成、流密码等方面有着广泛的应用。自从2004年密码学家王小云教授宣布攻破常用的MD5杂凑算法以来，网络信息安全问题进一步凸显。美国国家标准与技术研究所(NIST)于2007年宣布一项公开征集杂凑函数新标准(SHA-3算法)的活动，于2012年10月2日Keccak杂凑算法凭借着其新颖的Sponge结构迭代设计方法、较强的安全性能以及良好的实现方法成为新一代杂凑函数标准。

    作为当前杂凑算法标准的SHA-3算法，与以往哈希算法相比呈现出良好的安全性和工作效率，但其物理实现还不太成熟。首先，算法的电路实现所占用的硬件资源仍相对较多；其次，算法实现所能达到的处理速度虽已较快，但实际应用空间仍有限；最后，随着攻击方式的进化，SHA-3算法被攻击的轮数会越来越多，其安全性也可能随之降低。因此，SHA-3算法本身存在一定的优化空间。本文在研究查找表（Look-Up-Table，LUT)方法的基础上，针对算法在实际应用中速度慢与占用资源大的问题进行改进，提出一种基于LUT的高速低硬件开销SHA-3算法。将其运行的中间结果先写入RAM中，每轮运算只需输入地址信息就能实现具体逻辑运算，同时利用硬件共用的方式提高硬件利用率。改进后的算法进一步提高SHA-3算法的适用性，具有广阔的应用前景。

1 SHA-3算法

    2012年10月NIST宣布Keccak算法为SHA-3竞选的最终获胜者，该算法方案的提供者主要包括Guido Bertoni，Joan Daemen(AES加密算法的发明者之一)，Michael Peeters以及Gilles Van Assche。所提供标准的Keccak方案整体结构采用海绵结构(sponge construction)。海绵结构的工作过程主要分成两个阶段：吸收阶段和挤压阶段。在吸收阶段，在保存内部状态不变的前提下将输入信息与输入状态进行异或操作，异或的结果作为吸收阶段的输入数据；在挤压阶段，根据输出数据位宽要求，从N轮置换运算的结果中交替取出所需数据，最后拼接成输出数据。Keccak算法所采用的海绵结构模型。其中，压缩函数为Keccak-f[x]，x是轮函数的置换宽度，长度决定迭代函数的轮数，具体根据公式x=25×2l进行计算。即nr=12+2l，在压缩函数处理时，每一轮置换函数f作用在一个三维矩阵的五步迭代置换。

1.1 SHA-3算法的三维置换矩阵

    压缩函数Keccak-f[x]的输入数据按照坐标轴m、n、p依次填充进5×5×64的三维比特数组a[m][n][p]中，称作状态数组。最终提交时，b=1 600，即m=5，n=5，p=64(l=6)，基本块置换函数由12+2l(l=6时为24)轮迭代5个子轮，每轮运算都各自简单独立。每轮迭代的轮函数由五步迭代的R运算组成，通过对三维比特数组进行不同方向的变换达到扩散和混淆的作用。其中，变换为非线性变换，下文将会具体分析SHA-3算法的五步迭代函数。

1.2 SHA-3算法的五步迭代函数

    目前SHA-3算法的三维矩阵主要采用l=6，即矩阵大小为5×5×64。在m、n轴进行模5运算，在p轴进行模64运算。

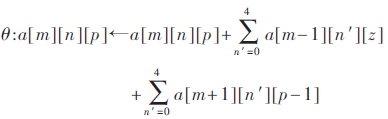
    这一变换是将每比特附近的两列(column)比特之和迭加到该比特上(m和n的坐标都是模5的)具有良好的扩散性。

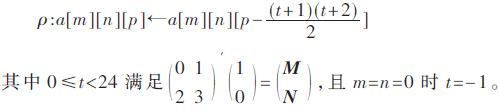
    这一变换作用于z轴上，是针对每个p方向的lane的比特循环移位。

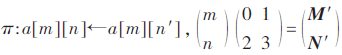
    这一变换是针对每个m-n平面的slice的比特移位，达到长期扩散的效应。

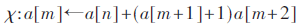
    这是针对每个m方向的row的非线性运算，等效为5×5的S盒。

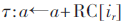
    这一变换是通过在每轮运算最后加一个轮常数RC，逐比特进行，且每轮i_r的轮常数不同，达到破坏三维数组原有对称性的效应。

2 SHA-3面积优化算法的VLSI实现

    SHA-3算法的面积优化的主要思路是通过使用LUT方法达到使用并行加速设计算法的效果，利用RAM寄存每次计算结果以及一些中间变量，实现同时对一个分组数据进行运算处理，从而加快SHA-3置换算法处理速度，降低算法执行功耗。

2.1 LUT面积优化策略

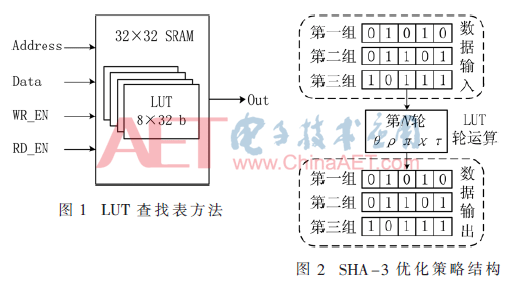
    由于在SHA-3算法中，分组数据位宽均为64位，因而若采用并行加速的方式来设计算法，开销太大不能实现同时对一个分组数据进行运算处理，在运算过程中只能对某一部分数据进行运算，其他数据资源处于闲置状态，极大影响利用率和算法执行速度。而采用LUT方法，如图1和图2所示，暂存中间数据来实现算法，克服内存开销过大的缺点。每次将计算好的结果放在RAM中，进行加密运算时，直接从SRAM中取出运算结果即可。不但加快SHA-3置换算法处理速度，而且极大降低算法设计复杂度，进而减少实际电路资源开销。

2.2 面积优化算法流程

    基于SHA-3标准算法和面积优化策略，确定SHA-3面积优化算法的具体实现方案，该算法的流程如图3所示，该算法步骤如下：

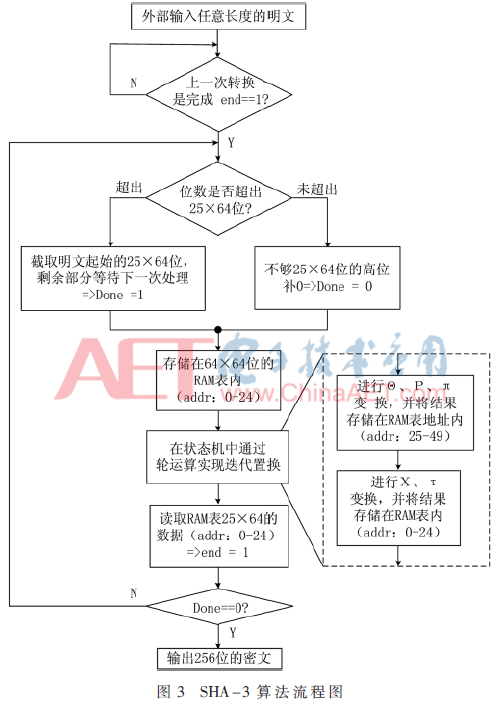
    步骤1：将算法中输入的25位64进制数据形式的输入数据从0地址开始存入64位64进制的RAM表中。

    步骤2：通过状态机对输入数据依次实现线性变换以及非线性变换，每次运算的结果都存储在RAM表中，每个状态都会产生一个0~63的地址addr、一个8位2进制的命令字command、0~4的控制字counter_plane_to_pe和counter_sheet_to_pe、一个0~24的轮转数nr_round以及2个一位二进制读写信号enR和enW，通过地址以及读写信号对RAM表中对应的数据进行操作，读取的数据存储在64位的二进制寄存器data_from_mem中，要写入RAM表中的数存储在64位的二进制寄存器data_to_mem中。

    每个状态执行的变换过程如图4所示，变换进行的运算使用了9个64位的二进制寄存器，分别是r1_in、r1_out、r2_in、r2_out、r3_in、r3_out、rho_out、chi_out、iota，初值均为0x0000。变换流程图如图3所示，主要分成以下两个阶段：

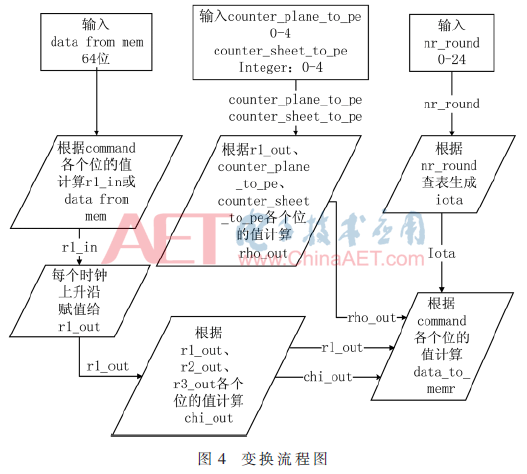
    阶段1：当enW=1时，在执行线性变换阶段，根据command命令字各个位的值选择data_from_mem、r1_out、r2_out、r3_out进行对应的与、异或运算计算出r1_in的值，根据command命令字各个位的值选择r1_out或r2_out赋值给r2_in，根据command命令字各个位的值选择r2_out或r3_out赋值给r3_in，将r1_out、r2_out、r3_out进行对应的与、异或运算计算出chi_out的值；在执行非线性变换阶段，根据counter_plane_to_pe、counter_sheet_to_pe控制字的值将r1_out左移一定位数后赋值给rho_out，在执行变换阶段时，根据轮转数nr_round生成对应的轮常数iota。

    阶段2：当enR=1时，根据command命令字各个位的值选择将r1_out、chi_out、rho_out与iota进行异或运算后赋值给data_to_mem。当时钟上升沿到来时，按照五步迭代公式赋值运算。将RAM表中地址0~24的数据输出，得到最终SHA-3数据。

2.3 面积优化算法的硬件结构

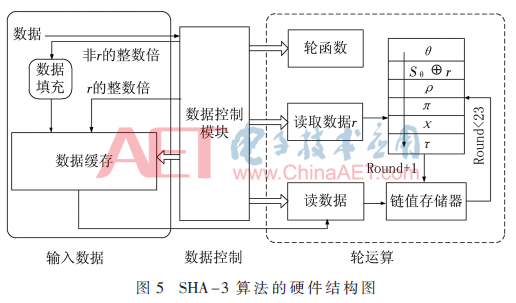
    面积优化SHA-3算法的具体结构如图5所示， HA-3算法的主要开销在轮运算过程中，所以处理速度的快慢由24轮运算的五步迭代所决定。因此，考虑在硬件实现过程中，在一个时钟周期内采用LUT的方法完成五步迭代，提高算法的效率。同时采用硬件复用的方式，进行面积优化。从时间的角度，可以提前完成各轮密匙的计算，杂凑数据时只需要一个时钟周期即可，所以数据计算可以尽量满足对实时性的要求；从硬件开销角度看，整套SHA-3算法采用LUT和硬件复用的方式，节省大量的存储和逻辑运算单元，降低系统功耗。

3 实验结果与分析

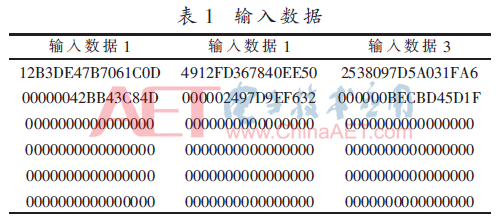
    采用TSMC 65 nm CMOS工艺，实现基于LUT方法的SHA-3算法硬件电路。实验环境包括Intel Pentium(R) Dual-Core CPU 2.70 GHz、2 G RAM计算机，DC综合软件，NCverilog和Modelsim仿真软件。采用VHDL语言实现面积优化SHA-3算法，其中表1和表2分别为部分的输入/输出数据，表3为DC综合的特征总结，工作速度为150 MHz。

4 结论

    本文通过对SHA-3算法的五步置换研究，提出一种基于LUT方法的小面积算法设计方案，并在VHDL硬件语言下实现。将生成数据与原有的SHA-3算法结果进行比较，验证其正确性。采用利用状态机实现SHA-3算法核心置换函数的轮运算，结合LUT方法处理每轮运算的数据交换和数据存储，对RAM表读写数据实现读取运算与覆盖新的运算结果，在优化SHA-3算法效率的同时有效降低面积开销。

参考文献

[1] 王勇，蔡国永.基于随机函数的哈希函数[J].计算机工程与设计，2015，34(10)：2679-2683.

[2] ZHANG H，HAN W，LAI X，et al.Survey on cyberspace security[J].Science China(Information Sciences)，2015，58(11)；5-47.

[3] MALIK A，AZIZ A，KUNDI D，et al.Software implementation of standard hash algorithm(SHA-3) Keccak on Intel core-i5 and cavium networks octeon plus embedded platform[C].2nd Mediterranean Conference on Embedded Computing (MECO)，2013：79-83.

[4] Hash function[OL].http：//en.wikipedia.org/wiki/Hash function.(2015.11.30).

[5] 李倩男，李云强，蒋淑静，等.Keccak类非线性变换的差分性质[J].通信学报，2012，33(9)：140-146.

[6] 李建瑞，汪鹏君，张跃军，等.基于SHA-3算法的图像密钥生成方法[J].华东理工大学学报，2015，41(5)：693-697.

作者信息:

张跃军，廖澴桓，丁代鲁

（宁波大学 电路与系统研究所，浙江 宁波315211）