0 引言

    随着电子信息产业的蓬勃发展，便携式电子产品的耗电量越来越大。在电池本身技术短期内无法取得重大突破的前提下，无线充电技术成为一种可行且便利的解决方式。目前，磁感应式和电磁谐振式无线充电受到广泛关注^[1-3]。相比于磁感应式无线充电，电磁谐振式不仅可以进行中短距离的充电，还能支持多个设备同时充电，且充电功率也有很大提升^[4-6]。

    无线充电区域内可能存在多个不同种类的待充电设备，这些设备往往同时充电^[7]。每个设备理论上能获得均等的充电机会，但当接收端类型各异时，发射端往往无法根据实际需求进行无线供电，因此想要提高无线充电效率，有必要在充电之前或充电过程中对设备进行优先级排序^[8-10]。本文基于电磁谐振式无线充电原理，考虑多设备同时充电场景，提出一种优先级算法。该算法可以有效地优化一对多无线充电，提高充电效率。

1 场景理论分析

1.1 系统模型

    首先，假设在一定范围内的设备才能被充电。其次，发射端线圈和接收端线圈在充电范围内相互平行。无线充电功能模型如图1所示。接收端通过蓝牙将信息反馈给发射端。本文中，蓝牙的工作范围大于充电范围，且蓝牙设备均运行良好。

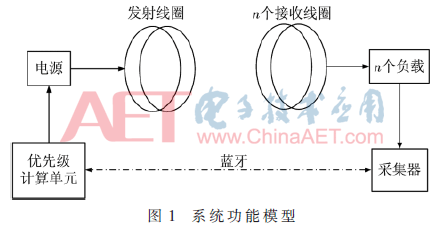
    图1中，采集器实时采集接收端的信息，优先级计算单元根据采集结果实时更新充电优先级并控制充电，使充电优先级的计算和更新与环境的实时变化密切地联系起来。

1.2 谐振式无线充电

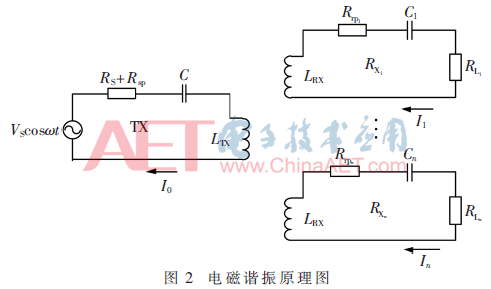
2 优先级算法

    优先级算法的主要目的是减少充电时间、提高充电效率等。本文所提出的优先级是一种动态过程，优先级高的任务最先得到执行；每当有新设备需要充电时，也会根据所有设备的情况重新分配优先级。

    充电范围内的设备有充电和待充电两种状态。当设备的优先级最高或充电范围内仅有一个设备时，该设备处于充电状态，而其他设备则处于待充电状态。当设备处于待充电状态时，接收端线圈电路断开，设备完全不会被充电也不会与其他接收端线圈发生耦合。当设备充满电后，设备的状态切换至待充电状态。

    本文提出一种基于多参数的优先级算法，该算法的基本思想如下：

    (1)无线充电范围内的设备能参与优先级判断；

    (2)充电时间相对短的设备可以被优先充电；

    (3)小功率要求的设备(即负载功率小的设备)优先级高，可以被优先充电；

    (4)离发射端线圈相对近的设备优先级较高。

    本文的动态优先级如式(2)所示。

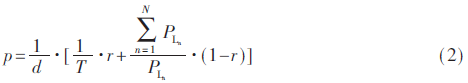
    式中，p为优先级，d为接收端与发射端之间的距离，为设备的负载功率(功率要求)，T为充电时间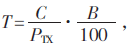，其中P_TX为发射端功率，B为设备的残余电量，C为设备的电池容量（单位为Wh）。式(2)中r(r∈[0，1])为主观系数，即参数对系统的影响比重，由用户决定。r<0.5时功率要求对系统影响大，功率要求优先，反之充电时间优先。换言之，r=0.5是用户决定充电时间优先还是功率要求优先的临界值。

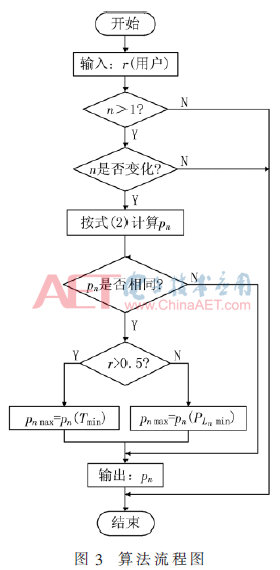
    优先级算法的流程图如图3所示。图中p_n是不同设备的优先级。当p_n相同时，需根据主观系数r来进行优先级判断。图3中T_min和分别表示充电时间少和负载功率小的设备，其中p_{n max}=p_n(T_min)表示充电时间少的设备优先级高，同理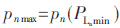表示负载功率小的设备优先级高。

    根据电磁谐振电路原理图(图2)，加入优先级算法的充电效率如式(3)所示。

    相比于式(1)，对接收端依次充电可以提高整个充电系统的充电效率。

3 仿真分析

    本文针对图1所示的无线充电系统功能模型，对不同接收端进行优先级算法仿真。假设发射端功率P_TX为20 W，对以下5种情况进行仿真分析。

3.1 充电时间

    充电时间在充电系统中是人们最关注的因素之一。充电时间取决于电子设备的电池容量、残余电量和发射端功率等，如式(3)所示。

    假设充电区域内有三个不同电池容量的设备，分别为3 Wh、15 Wh和30 Wh；三个设备的负载功率相同，均为5 W；离发射端的距离均为5 cm。主观系数r为0.5时，优先级与残余电量的关系图如图4所示。由图知，电池容量越小，残余电量越少的设备优先级越高，即充电时间越短的设备优先级越高，可以被优先充电。

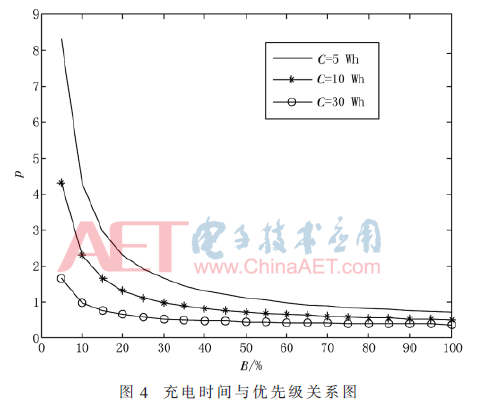
3.2 负载功率

    负载功率是设备本身消耗的电功率，即设备的功率要求和能量需求，负载功率在充电系统中是一个关键因素。

    假设有三个负载功率不同的设备，两个设备的负载功率固定，为5 W和10 W，另一个设备负载功率在变化；充电时间相同，电池容量为3 Wh，残余电量为10%；充电距离均为5 cm。主观系数r为0.5时，优先级与负载功率的关系图如图5所示。

    由图知，对于负载功率变化的设备，负载功率越小，优先级越高，因其需要的能量少；对于负载功率固定的设备，优先级随着负载功率的增加而增加，因三个设备的负载功率和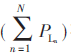在增加。负载功率固定的两设备优先级随负载功率的增加呈直线上升，且上升的幅度不一致，负载功率为5 W的设备能量需求少，故优先级增加的幅度大。设备的负载功率在变化的过程中优先级在不断地变化，三条曲线相交于P₁和P₂点处，负载功率大于10 W(P₂右端)时优先级最低，小于5 W(P₁左端)时优先级最高，反之介于两者之间，负载功率相同，优先级相同，即图5中的P₁和P₂点。

3.3 充电距离和主观系数

    在无线充电中，电子设备与发射端之间的距离起着重要的作用。假设有三个不同的设备，充电时间和功率要求各不相同。三个设备的电池容量均为10 Wh，残余电量分别为10%、80%和10%，负载功率分别为5 W、5 W和20 W。主观系数r取不同值，优先级与充电距离的关系如图6所示。

    由图知，接收端设备离发射端越近，优先级越高，与设备的充电时间和功率要求无关，也不随主观系数变化。

    主观系数r取不同值时，三个设备的优先级各不相同，主观系数r决定充电优先（充电时间优先或功率要求优先），由用户主观决定。图6中，主观系数r的大小对设备的充电优先级影响很大，如左上r为0.1时的图，残余电量为10%的设备充电时间少，理论上应比残余电量为80%的设备优先级高，但用户注重功率要求，故残余电量为80%的设备优先级高，因其负载功率小，功率要求低；当r为0.9时，如右下图所示，残余电量为10%的两个设备，即使两设备的负载功率不同，优先充电的等级却相同，因为用户注重充电时间，功率要求对用户来说不太重要，故负载功率不同残余电量相同的两设备优先级相同；主观系数r增加时，虽然负载功率为20 W的设备功率要求大，能量需求多，但该设备优先级仍然随之增加，因用户越来越注重充电时间，该设备的残余电量仅为10%，充电时间相对短，故该设备的优先级随着主观系数r的增加而增加。

3.4 时间

    充电时间是充电开始到充电结束的时间间隔，优先级在这段时间间隔内随时间的变化而变化。

    假设三个设备的充电距离相同，充电时间不同，电池容量均为10 Wh，残余电量分别为40%、60%和50%；功率要求不同，负载功率分别为3 W、6 W和10 W。主观系数r为0.5，随着时间的变化，三个不同设备的充电优先级如图7所示。

    发射端根据优先级排序对设备依次进行充电，设备1因优先级最高而被优先充电，处于充电状态，此时设备2和3处于待充电状态。在充电过程中设备1的优先级在不断的提高，因充电时间减少，功率要求降低。设备1充满电后切换至待充电状态，设备2和3根据优先级依次充电。设备充满电后不参与优先级判断，参与优先级判断的设备负载功率和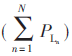减少，故优先级会有稍许降低。

3.5 有无优先级间的比较

    根据式(1)和式(4)对系统有无优先级算法进行仿真，如图8所示。从图中看出，相比于无优先级算法的无线充电系统，加入优先级算法使系统充电效率提高了20%。

4 结论

    本文基于电磁谐振式无线充电场景，通过优先级的研究，提出了一种混合型动态优先级算法，并分析了优先级对整个充电系统的影响。在算法中，本文考虑了设备的充电时间、负载功率、充电距离、主观系数和时间与优先级的关系，此外，还将有无优先级算法对无线充电的充电效率进行对比。充电时间越短，功率要求越小，充电距离越近的设备优先级越高，可以优先充电。仿真结果也验证了本文提出的优先级算法可以使得无线充电的效率大大提高。

参考文献

[1] 贾旭平.无线充电的主流技术[J].电源技术，2013，37(7)：1101-1104.

[2] CANNON B L，HOBURG J F.Magnetic resonant coupling as a potential means for wireless power transfer to multiple small receivers[J].IEEE Transactions on Power Electronics，2009，24(7)：1819-1825.

[3] WANG J，HO S L，FU W，et al. Finite-element analysis and corresponding experiments of resonant energy transfer for wireless transmission devices[J].IEEE Transactions on Magnetic，2011，47(5)：1074-1077.

[4] FU M F，ZHANG T，MA C B，et al.Efficiency and optimal loads analysis for multiple-receiver wireless power transfer systems[J].IEEE Transactions on Microwave Theory and Techniques，2015，63(3)：801-812.

[5] KIM E K，TECK C B，TAKEHIRO I，et al.Impedance matching and power division using impedance inverter for wireless power transfer via magnetic resonant coupling[J].IEEE Transactions on Industry Applications，2014，50(3)：2061-2070.

[6] 任立涛.磁耦合谐振式无线能量传输功率特性研究[D].哈尔滨：哈尔滨工业大学，2009.

[7] AHN D，HONG S.Effect of coupling between multiple trans-mitters or multiple receivers on wireless power transfer[J].Industrial Electronics，IEEE Transactions on，2013，60(7)：2602-2613.

[8] 刘怀，胡继峰.实时系统的多任务调度[J].计算机工程，2002，28(3)：43-44，150.

[9] 金宏，王宏安，王强，等.改进的最小空闲时间优先调度算法[J].软件学报，2004，15(8)：1116-1123.

[10] 巴巍.实时系统动态优先级任务调度算法的研究[D].大连：大连理工大学，2010.

作者信息:

刘  璐1，郝  鹏2，刘维亭1，俞玲娜1

(1.江苏科技大学 电子信息学院，江苏 镇江212003；2.镇江博联电子科技有限公司，江苏 镇江212001)