张家生,崔鹏鹏,沈忱,韩迎鸽
(安徽理工大学 电气与信息工程学院,安徽 淮南 232001)
摘要:针对基于CMA的DFE盲均衡算法收敛速度慢、收敛后稳态剩余误差大的缺点,提出了一种改进的基于CMA的DFE盲均衡算法。该算法通过引入均方误差作为调整步长的参量,构造出指数型变步长函数,把基于CMA的DFE盲均衡算法中前馈滤波器和反馈滤波器更新方程中的固定步长值变为可变值,并对其收敛性做了分析。计算机仿真表明,改进算法具有较快的收敛速度和更小的剩余误差。
关键词:CMA;码间干扰(ISI);判决反馈均衡器(DFE);变步长
中图分类号:TN911文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.09.021
引用格式:张家生,崔鹏鹏,沈忱,等.一种改进的变步长常模判决反馈盲均衡算法[J].微型机与应用,2017,36(9):71-73,77.
0引言
高速数据通信系统中,码间干扰是影响通信质量的主要决定因素,为了消除码间干扰(Inter Symbol Interference, ISI),必须进行信道均衡。盲均衡由于不需要发送训练序列引起了各国学术界以及通信业界的高度重视。在各种盲均衡算法中,基于常数模算法(Constant Modulus Algorithm,CMA)的判决反馈盲均衡(Decision Feedback Equalization,DFE)由于反馈滤波器部件具有非线性特性,能在有效消除ISI的同时不引入增益噪声[12],因此得到了广泛应用。但是在许多情况下相对于CMA,DFE的收敛速度和稳态性能改善得并不明显,尤其在信号的模值不是常数的情况下。这是因为基于CMA的DFE采用的是固定步长的常数模算法,而对于非常模信号,在星座图中的任何一个信号都无法使CMA的代价函数为零,因此基于CMA的DFE就会发生过调,导致收敛慢,收敛后稳态误差较大[34]。
为了提高基于CMA的DFE的收敛速度,减小稳态误差,本文提出一种改进的基于CMA的DFE盲均衡算法,该算法通过引入均方误差作为调整步长的参量,把基于CMA的DFE盲均衡算法中前馈滤波器和反馈滤波器更新方程中的固定步长值变为可变值,以期获得较好的均衡效果和收敛性能。
1基于CMA的DFE算法
基于CMA的DFE算法由一个前馈滤波器和一个反馈滤波器组成,其中反馈滤波器由判决装置输出的判决驱动,其原理图如图1所示。
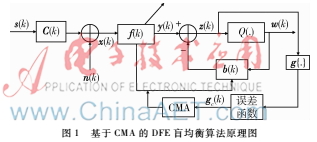
图1中,s(k)是独立同分布的发射信号序列;C(k)是信道脉冲响应;n(k)是高斯白噪声序列;y(k)是前馈滤波器输出;z(k)是判决器的输入;w(k)表示判决器的输出信号。
设前馈滤波器和反馈均衡器的输入信号向量分别为:
x(k)=[x(k),x(k-1),…,x(k-Lf+1)]T(1)
w(k)=[w(k-1),w(k-2),…,w(k-Ld)]T(2)
前馈滤波器和反馈均衡器的权系数向量分别为:
F(k)=[f0(k),f1(k),…,fLf-1(k)](3)
B(k)=[b0(k),b1(k),…,bLd-1(k)]T(4)
则由图1可知:
z(k)=FT(k)x(k)-BT(k)w(k)(5)
式中,Lf和Ld分别为前馈滤波器长度和反馈滤波器的长度,Lf、Ld均为正整数,T表示转置。
则基于CMA的DFE盲均衡算法的权系数迭代公式为:
f(k+1)=f(k)-ufe(k)z(k)y*(k)
b(k+1)=b(k)+ube(k)z(k)w*(k)(6)
式(1)~式(6)构成的算法称为基于CMA的DFE盲均衡算法。式(6)中,e(k)=|z(k)|2-R,R为常数模算法的模值,R=E[|s(k)|4]/E[|s(k)|2],‘*’表示共轭,uf和ub均为正实常数,分别为前馈滤波器和反馈滤波器更新方程中固定的迭代步长。即基于CMA的DFE算法采用的是固定步长的常数模算法来调整前馈滤波器和反馈滤波器的权系数。所以算法收敛慢,收敛后稳态误差较大。
2改进的基于CMA的DFE盲均衡算法
2.1算法原理
为了提高基于CMA的DFE盲均衡算法的收敛速度,改善其均衡性能,研究人员提出了变步长思想[57],即在保证收敛的情况下,在迭代初期为了加快收敛速度,步长取较大的值,在算法接近收敛时,为了减小稳态误差,步长取较小的值。根据这一原则,文献[5]提出了一种基于Sigmoid函数的变步长盲均衡算法,即构造了一个关于瞬时误差和步长因子的单调Sigmoid函数,改进算法不但具有较快的收敛速度且具有较小的稳态误差。但Sigmoid函数过于复杂,而且误差在接近零处变化太大,不具有缓慢变化的特性。对此本文对Sigmoid函数进行了改进,即通过引入均方误差作为调整步长的参量,构造出指数型变步长函数,具体表达式如下:
u(k)=c{1-exp[-d]}(7)
其中,c,d为正常数,用于调整算法收敛速度及稳态误差。
将式(7)代入式(6),则抽头系数权向量的更新方程变为:
f(k+1)=f(k)-u(k)e(k)z(k)y*(k)
b(k+1)=b(k)+u(k)e(k)z(k)w*(k)(8)
式(1)~(5)和式(8)构成的算法称为改进的基于CMA的DFE盲均衡算法。
2.2算法的收敛性分析
为了确保算法具有良好的收敛性和稳健性,步长因子必须满足:
0≤u(k)≤2/3tr(R)(9)
式(9)中,R代表输入信号的自相关矩阵,tr(R)代表该矩阵的迹。
由式(7)可知:
0≤1-exp[-d]}≤1(10)
所以有:
0≤c{1-exp[-d]}≤c(11)
即:
0≤u(k)≤c(12)
所以c的取值要满足:
c≤2/3tr(R)(13)
但满足该条件的所有c和d对于步长的取值大小存在着局限性,为此c和d的取值要由理论分析、仿真分析和试验来共同确定。
3仿真
为了验证新算法的性能,分别对基于CMA的DFE盲均衡算法和改进的基于CMA的DFE盲均衡算法进行了MATLAB仿真。
仿真环境:发射信号采用4QAM的调制信号,信噪比为25 dB,前馈滤波器长度为Lf=33,采用中心抽头初始化的方法;反馈滤波器长度Ld=17,抽头系数初始化为全零值;迭代次数N=4 000,蒙特卡洛次数取400。在两种不同的信道中对两种算法进行仿真。
3.1实验1
信道为:h=[-0.053,0.184,-0.35,0,0,1],基于CMA的DFE算法中前馈和反馈滤波器的迭代步长分别为0.000 75和0.06,改进的基于CMA的DFE算法中的步长按式(8)调整,变步长调整参数c、d分别为0.007和6.0,仿真结果如图2所示。

图2(a)表明改进的基于CMA的DFE盲均衡算法大概经过1 500次迭代收敛,而基于CMA的DFE盲均衡算法大概需要经过2 500次迭代之后才趋于收敛,新算法比原算法将近快了1 000步。另外,由图2(a)可知,改进的基于CMA的DFE盲均衡算法的稳态误差比较小。图2(b)、(c)表明,与基于CMA的DFE盲均衡算法相比,改进的基于CMA的DFE盲均衡算法输出信号星座图更加紧密集中、清晰,即改进算法取得了更好的均衡效果。
3.2实验2
信道为:h=[0.212 2,0.104,0.890 8,0.213 4,-0.15,-0.083],基于CMA的DFE算法中前馈和反馈滤波器的迭代步长分别为0.000 6和0.075,改进的基于CMA的DFE算法中的步长按式(8)调整,变步长调整参数c、d分别为0.007和7.0,仿真结果如图3所示。
图3(a)表明改进的基于CMA的DFE盲均衡算法大概经过2 000次迭代收敛,而基于CMA的DFE盲均衡算法大概需要经过3 000次迭代之后才趋于收敛,新算法比原算法快了1 000步左右。另外,由图3(a)可知,改进的基于CMA的DFE盲均衡算法的稳态误差比较小。从图3(b)、图3(c)可以看出,与基于CMA的DFE盲均衡算法相比,改进的基于CMA的DFE盲均衡算法输出信号星座图更加紧密集中、清晰,即改进算法取得了更好的均衡效果,具有更小的稳态误差。
4结束语
针对基于CMA的DFE盲均衡算法收敛速度慢、收敛后稳态剩余误差大的缺点,构造了一种改进的基于CMA的DFE盲均衡算法。该算法把基于CMA的DFE盲均衡算法中前馈滤波器和反馈滤波器更新方程中的迭代步长由原来的固定值改成可变值,即通过引入均方误差作为调整步长的参量,构造出指数型变步长函数。4QAM信号仿真结果表明,相对于固定步长的基于CMA的DFE盲均衡算法,改进算法不但具有较快的收敛速度而且具有较小的稳态误差。
参考文献
[1] 冯成旭,刘忠,罗亚松.稳健水声信道判决反馈盲均衡算法研究[J].火力与指挥控制,2014,39(6):5-6.
[2] 宁小玲,刘忠,罗亚松,等.一种改进的水声信道载波恢复盲均衡算法[J].西安电子科技大学学报,2012,39(1):151-152.
[3] 张银兵,赵俊渭,郭业才.抑制α稳定噪声的改进常数模盲均衡算法[J].西北工业大学学报,2010,28(2):202-206.
[4] 郭业才,王南南.基于修正模判决的多模盲均衡算法研究[J].计算机应用研究,2014,31(8):2454-2455.
[5] 刘建成,赵宏志,全厚德,等.迭代变步长LMS算法及性能分析[J].电子与信息学报,2015,37(7):1674-1675.
[6] 宋志雄,喻翌,赵海全.基于箕舌线函数的变步长自适应谐波电流检测算法[J].电力系统自动化,2013,37(22):54-59.
[7] 张红梅,韩万刚.一种新的变步长LMS自适应滤波算法研究及其应用[J].仪器仪表学报,2015,36(8):1822-1830.

