0 引言

    当代建筑，尤其是商业建筑中，用电器数量巨大并且种类繁多，这使得监测用电器的开/关状态非常具有挑战性。现有的监测方法大致可以分为两类：(1)高保真状态监测；(2)非侵入式负荷监测(NILM)。NILM的早期工作主要利用了稳态能耗转变^[1]，其主要思想是检测精确到用电器个体的动作和反应能耗模式中的跳变。因此它只适用于稳定且只有有限状态的用电器。之后，调和分析的技术被用于识别连续时间变化的用电器^[2]。最近的机器学习的技术，如支持向量机^[3]、人工神经网络^[4]、线性动态模型^[5]、模式识别^[6]、稀疏编码^[7]以及多种非监督的学习方法^[7-9]在NILM的领域有应用。

    本文创新性地应用了用电器的开闭状态在时域上高度相关的这一现象，研究了一个多电表的NILM系统。为了实现准确、高效且可大规模化的用电器状态解码，提出用隐马尔可夫模型将切换稀疏性和序列可行性限制嵌入到解码过程中,快速序列解码使得大量用电器状态的高效且准确的在线监测成为可能。

1 系统模型

    建筑物中的电网具有树状结构。电力负载树的根节点对应整个建筑物的总电闸，中间层对应电闸和配电箱，叶子节点对应终端用电器。在电力负载树上，一个节点的总能耗是以该节点为根的子树所包含的所有用电器的能耗总和。智能电表可以被部署在树的任何一个节点。

1.1 监测模型

    部署了m个电表在电力负载树中用于监测N个用电器的开闭状态时，每个电表实时监测位于其下的所有用电器的能耗总和。假设所有的电表同步运行，在t时刻，电表i的监测模型遵循以下公式：

1.2 压缩监测模型

    记Δ_t为指示N个用电器在t时刻状态是否改变的向量。Δ_t的稀疏性与采样区间的长度和时刻t相关，如早上和晚上开关时间发生更频繁，而较少发生在凌晨。因而，在不同的时间段选择相应的采样区间长度，使得用电器状态的切换次数至多为U_t，即||Δ_t||1≤U_r，其中U_t是一个小的整数且U_t<<N。

    通过电表的差分测量Γ解码Δ的问题，可以通过带L1范数约束的最小二乘估计解决。

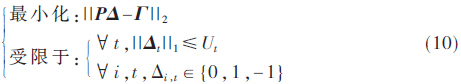
2 基于隐马尔可夫模型的序列监测算法

    通过观察发现，用电器状态的转移具有马尔可夫性，即一个用电器在t时刻的状态仅与t-1时刻的状态相关。其状态不能被直接观察到，但是可以通过智能电表测量总能耗推测得到。于是状态解码问题式(10)可以由一个马尔可夫模型表示为：λ=(X₀，A_t，B)，其中X₀是初始状态分布；A_t是状态转移矩阵，B是观测矩阵。

    考虑A_t是时变的，A_t中的一个元素a_i，j，t=P(X_t=S_j|X_t-1=S_i)，i，j∈(1，2，…，2^N)表示在第t-1时刻由状态S_i变到S_j的概率。B的元素b_i，j=P(Y_t=v_i|X_t=S_j)表示状态当观察到v_i时S_i的似然，其中v_i∈V={v₁，v₂，…，v_M}，且V是电表所能得到的所有不同观测值的结合。由这样一个隐马尔可夫模型，状态序列解码问题可以被表述为：

    问题1：给定m个电表在时刻1～t的能耗测量值：Y={Y₁，Y₂，…，Y_t}，以及隐马尔可夫模型λ，求N个用电器的状态序列X={X₁，X₂，…，X_t}，使得如下条件概率被最大化：

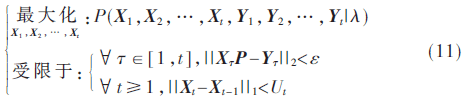
在第一个约束中，ε是一个智能电表可以接受的最大测量误差；第二个约束表征了式(10)中的状态切换的稀疏性。

2.1 快速序列解码算法

    式(11)中的隐马尔可夫模型总共有2^N种状态，且序列长度为t，用于计算最可能的隐序列的传统Viterbi解码算法需要O(t2^2N)时间，这对于N较大的情况是无法承受的。

2.2 快速向前搜索策略

2.3 快速反向搜索策略

    在通过前向搜索得到一个可行状态x_t后，需要通过式(15)使用一个回溯算法来找到一个最佳路径的权重γ(x_t)。由状态转移模型A_t可知，从x_t到一个前驱x_t-1的边权重可以通过下式计算：

3 性能评价

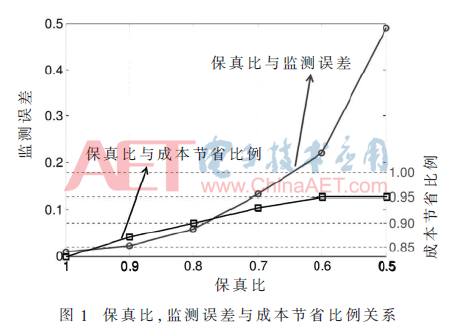
    基于的隐马尔可夫模型的NILM方法，考察保真比例对于监测精度的影响。为了专注于探讨保真比例的影响，电表噪声σ被设为0，因此所有的误差都是由解码的模糊性造成的。监测精度、保真比例与对应的成本节省比例的关系在图1中展示，这些结果显示出了压缩状态监测问题的一些有趣的性质。成本节省比例随着保真比例的下降缓慢上升，当保真比例小于0.6了之后到达一个饱和状态。监测误差随着保真比例的上升快速上升。两条曲线不同的趋势指出了保真比例的较好的区域，在其中监测误差很小且大多数部署成本可以节省，如图中保真比(clear ratio) 0.8～1的区域。

    上述实验都假设用电器都具有静态的模式。接下来在PowerNet^[10]的数据集上的实验突破了这一限制。

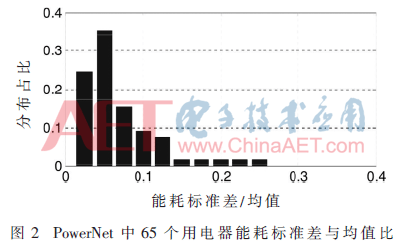
    首先建立用电器的能耗模式。通过对每个用电器的500 s采样的统计分析，其标准差与均值的比例被计算出来，且被展示于图2中。可以看出多过75%的用电器的标准差与均值的比例小于0.1，表明了现实中的用电器的能耗并没有表现出高度动态。

    对于在线部分的计算，当一个用电器被打开时，其能耗并不是静态的而是符合数据集中的一个能耗轨迹。每个电表测量其子树的所有用电器的能耗， 并将相邻30 s读数的平均值用于解码所有用电器的状态。快速序列解码算法和Viterbi算法的状态监测性能的对比可以在图3中看到。

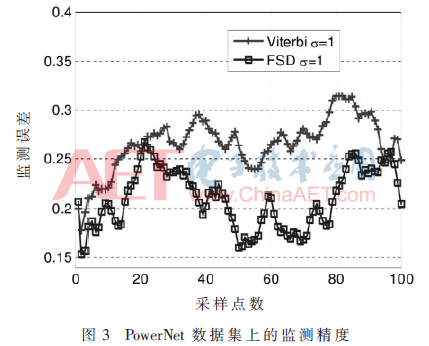
    通过仔细选取电表部署方案，可以保证解码误差通常都在20%以下，同时它具有很高成本节省比例，这表明了所提出的多电表的NILM框架在动态能耗用电器的状态解码中具有巨大潜力。仔细检查了解码错误的原因，发现其主要是因为某些大型用电器的开闭状态变化会掩盖小型用电器的变化。这样的问题可以通过改进部署方案及同时考虑不同用电器的均值和方差来达到，这将是未来的一个研究方向。

4 结束语  

    本文介绍了一个用于检测大量用电器开闭状态的序列解码框架。其主要思想是利用用电器的一些基本性质，如用电器的能耗模式可以离线学习，并且用电器在短时间内开闭状态的切换是稀疏的。提出了一个快速序列解码算法用以提高分辨2^N种状态在时间上的效率。实验结果验证了该算法的有效性和正确性。

    这项工作包含了一些基本假设,例如能耗模式是静态的，状态转移概率是独立同分布的。在未来工作中，可以考虑更加复杂的能耗模式和更加有效的部署算法。状态转移可以进一步被推广到隐式半马尔可夫模型以考虑用电器的持续时间的分布。瞬时信号的检测可以用来找到状态切换的发生时机，而将关联的开闭事件组合起来，可以进一步提高解码精度。

参考文献

[1] LAUGHMAN C，LEE K，COX R，et al.Power signature analysis[J].Power and Energy Magazine，IEEE，2013，1(2)：56-63.

[2] LEE K D，LEEB S B，NORFORD L K，et al.Estimation of variable-speed-drive power consumption from harmonic content[J].Energy Conversion，IEEE Transactions on，2015，30(3)：566-574.

[3] 刘晓明，饶翚.基于OGSA的网格工作负载监测系统研究[J].电子科技大学学报，2007(5)：824-826，857.

[4] PATEL S N，ROBERTSON T，KIENTZ J A，et al.At the flick of a switch: Detecting and classifying unique electrical events on the residential power line[C].Proceedings of Ubi-Comp 2007：ubiquitous computing.Springer，2007：271-288.

[5] KOLTER J Z，BATRA S，NG A Y.Energy disaggregation via discriminative sparse coding[C].Proceedings of Advances in Neural Information Processing Systems，2014：1153-1161.

[6] DONG R，RATLIFF L，OHLSSON H，et al.A dynamical systems approach to energy disaggregation[C].Proceedings of Decision and Control(CDC)，2013 IEEE 52nd Annual Conference on.IEEE，2013：6335-6340.

[7] SHAO H，MARWAH M，RAMAKRISHNAN N.A temporal motif mining approach to unsupervised energy disaggregation[C].Applications to Residential and Commercial Buildings.Proceedings of AAAI，2013.

[8] PARSON 0，GHOSH S，WEAL M，et al.Non-intrusive load monitoring using prior models of general appliance types[C].Proceedings of AAAI，2012.

[9] KOLTER J Z，JAAKKOLA T.Approximate inference in additive factorial hmms with application to energy disaggregation[C].Proceedings of International Conference on Artificial Intelligence and Statistics，2012：1472-1482.

[10] PowerNet.Stanford PowerNet project[EB/OL].http：//powernet.stanford.edu/.2015.

作者信息:

蒋炜华，马临超，郑先锋

（河南工学院 电气工程系，河南 新乡453000）