0 引言

    传统的时频方法在处理非平稳信号时无法得到信号蕴含的全部信息等问题，使得相关学者致力于找到一种适合处理非平稳信号的新的时频分析技术。而2005年SMITH J S^[1]提出局部均值分解(Local Mean Decomposition，LMD)，似乎为解决这一问题找到了一个良好途径。LMD分解信号后可以产生多个具有物理含义的生产函数(Production Function，PF)分量，这些PF分量一般由包络信号和纯调频信号构成，通过组合幅值和瞬时频率就可以得到原信号的完整时频图^[2-4]。LMD被提出以来，相关学者发现LMD方法存在较为明显的端部效应。国内外学者针对这一问题提出了诸多解决方法，如镜像法、神经网络法、自回归法以及波形匹配法等等^[5-12]。其中镜像拓展法效果稍占优势，但镜像拓展法需要将镜面放置极值点处，而BP神经网络具有良好泛化能力，极易找到信号端部的极值点^[13-16]。鉴于此，本文提出基于BP神经网络与镜像技术相结合来处理LMD方法的端部效应问题。

1 LMD算法及端部效应

    局域均值分解的基本流程如图1所示，信号不断筛选就可以得到原始信号的全部PF分量。图中，x为原始信号，h、u为变量，a_i为包络函数，PF_i为生产函数分量，s_i为纯调频函数，n_i为局部极值点，m_i为局部均值函数^[1-3]。

    对于待分解信号x(t)，其计算步骤如下^[1-4]：

    (1)首先提取带分解信号的局部极值点，找到每个相邻局部极值点的平均值：

    对s₁₁(t)重复上述步骤，便可获得s₁₁(t)的包络估计函数a₁₂(t)。若局部包络函数a₁₂(t)不等于2，则说明s₁₁(t)不是纯调频信号，重复上述步骤获取的s_1p(t)为纯调频信号，于是：

2 基于镜像延拓和BP神经网络的端部效应处理方法

2.1 神经网络的数据序列预测模型

    BP神经网络算法就是利用BP算法来对神经网络进行训练，神经网络具有三层，分别为输入、输出和中间层，经验表明，中间层一般选取一个即可，具体如图2所示。

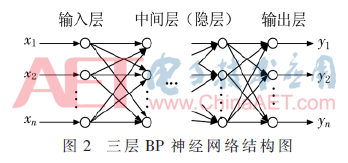
    BP神经网络基本步骤如下：

    (9)随机选取样本提供给网络，返回到步骤(3)，直到满足要求。基本思路如图3所示。

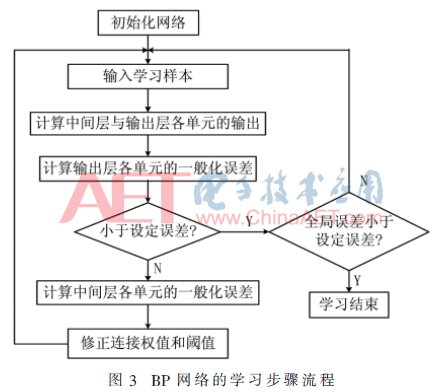
2.2 镜像延拓法

    为了更加显著消除端部效应，必须将镜面放置在极值点处，再根据信号特点决定放置镜面的具体位置。最后两端放置镜面的原信号的像将和原信号构成连续封闭的环状，如此原信号上下包络线将完全通过内部数据来得到，可以避免端部效应发生，故本文利用该方法来处理LMD的端部效应^[11-16]。

2.3 基于BP神经网络和镜像延拓闭合的端部效应处理方法

    本文首先通过BP神经网络方法预测得到原始信号的两端处的极值点，再利用镜像法对原信号形成闭环，最后将其运用到LMD分解过程中出现的端部效应抑制中。基本步骤如下^[10-14]：

    (1)以原始信号数据作为样本，训练得到BP神经网络预测模型。

    (2)以信号左端预测为例，通过步骤(1)得到的预测模型对原始信号进行预测，也就是通过x_q-n+1，…，x_q预测x_q+1，再将x_q+1代入到BP神经网络模型中，以x_q-n+2，…，x_q+1预测x_q+2，如此反复。右端预测同理。

    (3)判断步骤(2)得到的预测点是否为极值点。若为极值点，停止预测，否则继续预测，从而得到全部预测序列x_q，…，x_q+p。

    (4)将“镜面”放置步骤(3)得到的极值点处，使得原始信号形成闭环数据，再利用LMD对此信号进行分解。

3 仿真信号实验及结果分析

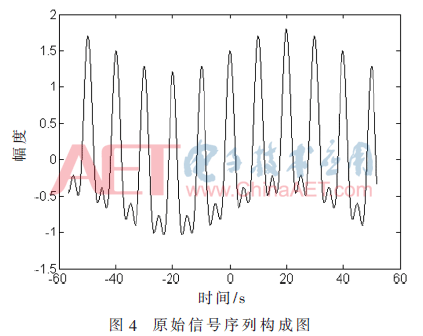
    构造仿真信号为：s(t)=0.5cos(0.4π·t)+cos(0.2π·t)+0.3sin(0.025π·t)，t∈[-57，52]，其信号如图4所示。这里，仅用镜像延拓进行端部效应处理，LMD分解得到PF分量及其误差分别如图5和图6所示。从图5和图6可以看出，LMD分解得到的各个PF分量与原信号之间误差不是很大，但是端部效应仍然比较明显。

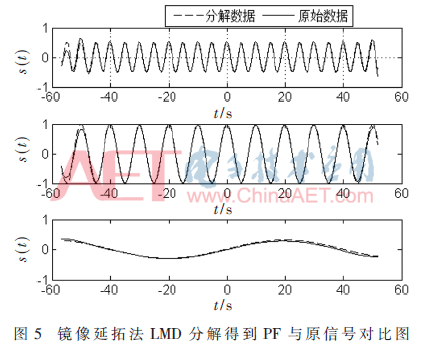
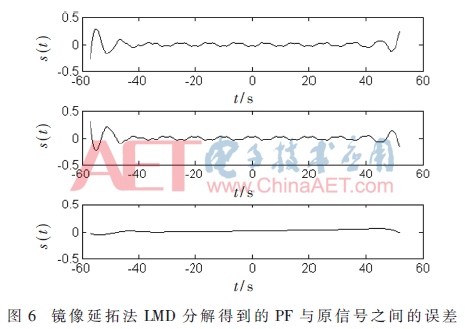
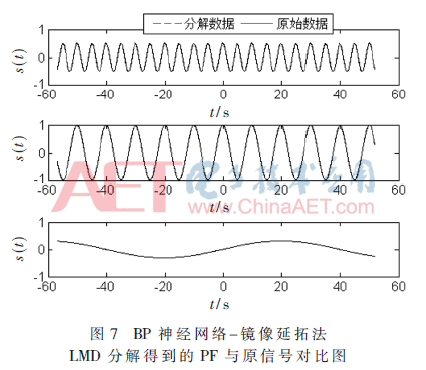
    采用本文提出的BP神经网络—镜像延拓法对图1所示信号进行LMD分解，各PF分量与其真实构成的对比结果如图7所示，它们与原始信号之间的误差如图8所示。利用BP神经网络方法对左右端点进行延拓获取极大值点和极小值点时，所获得的效果较好。将图5和图6的结果进行对比，可以看出，利用BP神经网络函数拟合预测方法获取一个或者几个极大值点和极小值点后，通过镜像延拓法完全抑制了可能产生的端部效应，进而得到与原始构成信号更为吻合的各个PF分量。相对于图6所示传统镜像延拓方法进行LMD分解各PF分量与原始构成信号之间的误差而言，图8所示BP神经网络—镜像延拓方法LMD分解的误差小得多。

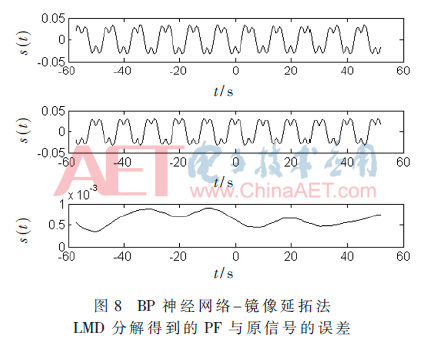
4 结论

    本文提出了利用BP神经网络进行数据序列延拓来抑制端部效应的一种新方法，所提出理论方法的要点在于通过BP神经网络函数拟合外推预测方法分别正向和反向延拓一个或者多个极大值点和极小值点，这样就可以将镜面放置在局部极值点上，然后再利用镜像延拓法进行端部延拓处理。它可以有效地抑制和消除LMD分解过程中可能出现的端部效应，分解得到的PF也能更好地反映原信号的真实信息和特征。仿真实验表明，BP神经网络-镜像延拓方法处理后进行LMD分解得到各个PF与原信号的构成信号之间的误差极小。这种方法能够适应不同信号分析的需要，具有极高的适应性和良好的推广价值。

参考文献

[1] SMITH J S.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface，2005，2(5)：444-450.

[2] HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London，Series A，1998，454(1971)：903-995.

[3] HUANG N E，WU Z，LONG S R，et al.On instantaneous frequency[J].Advances in adaptive Data Analysis，2009，1(2)：177-229.

[4] 程军圣，杨宇，于德介.局部均值分解方法及其在齿轮故障诊断中的应用[J].振动工程学报，2009，22(1)：76-84.

[5] WANG Y，HE Z，ZI Y. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis[J].Journal of Vibration and Acoustics，2010，132(2)：010-021.

[6] WANG Y，HE Z，ZI Y.A demodulation method based on improved local mean decomposition and its application in rub-impact fault diagnosis[J].Measurement Science and Technology，2009，20(2)：25-32.

[7] CHENG J，YANG Y.A rotating machinery fault diagnosis method based on local mean decomposition [J].Digital Signal Processing，2012，22(2)：356-366.

[8] WANG Y，HE Z，XIANG J，et al.Application of local mean decomposition to the surveillance and diagnostics of low-speed helical gearbox[J].Mechanism and Machine Theory，2012，47(1)：62-73.

[9] LIU H，HAN M.A fault diagnosis method based on local mean decomposition and multi-scale entropy for roller bearings[J].Mechanism and Machine Theory，2014，75(5)：67-78.

[10] FENG Z，ZUO M J，QU J，et al.Joint amplitude and frequency demodulation analysis based on local mean decomposition for fault diagnosis of planetary gearboxes[J].Mechanical Systems and Signal Processing，2013，40(1)：56-75.

[11] YANG Y，CHENG J，ZHANG K.An ensemble local means decomposition method and its application to local rubimpact fault diagnosis of the rotor systems[J].Measurement，2012，45(3)：561-570.

[12] YUAN B，CHEN Z，XU S.Micro-Doppler analysis and separation based on complex local mean decomposition for aircraft with fast-rotating parts in ISAR imaging[J].Geoscience and Remote Sensing，IEEE Transactions on，2014，52(2)：1285-1298.

[13] GUO Z，WU J，LU H，et al.A case study on a hybrid wind speed forecasting method using BP neural network[J].Knowledge-based systems，2011，24(7)：1048-1056.

[14] DING S，SU C，YU J.An optimizing BP neural network algorithm based on genetic algorithm[J].Artificial Intelligence Review，2011，36(2)：153-162.

[15] WONG W E，QI Y.BP neural network-based effective fault localization[J].International Journal of Software Engineering and Knowledge Engineering，2009，19(4)：573-597.

[16] REN C，AN N，WANG J，ET AL.Optimal parameters selection for BP neural network based on particle swarm optimization：A case study of wind speed forecasting[J].Knowledge-Based Systems，2014，56(3)：226-239.

作者信息:

王莉娜1，杨  剑2，孟庆强3

(1.江苏第二师范学院 数学与信息技术学院，江苏 南京210036；

2.江苏第二师范学院 信息化建设与管理办公室，江苏 南京210036；

3.南京南瑞集团信息通信技术分公司,江苏 南京210003)