陈富琴,周渊平
(四川大学 电子信息学院 ,四川 成都610065)
摘要:波达方向(Direct of Arrival,DOA)估计技术渐渐成为移动通信中的研究热点,当用户的信号方向未知时,可以根据经典算法多重信号分类(Multiple Signal Classification, MUSIC)和旋转不变技术信号参数估计(Estimating Signal Parameters Viarotational Invariance Techniques,ESPRIT)等方法估计信号DOA。针对不同的信号采取不同的算法分析。对窄带信号,从信噪比、阵元数、快拍数等不同情况下对TLSESPRIT算法和MUSIC算法进行了仿真实验,并比较了TLSESPRIT算法与MUSIC算法的DOA性能。对宽带信号,主要重点分析了基于非相干信号处理算法(Incoherent Signalsubspace Method, ISM)的两种改进的方法,对低信噪比子带赋予低权重或舍弃。通过仿真实验,证明了改进算法的优越性,同时对两种改进算法的使用场合作了简单的分析。
关键词:DOA;MUSIC算法;窄带信号;宽带信号
中图分类号:TN911文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.10.018
引用格式:陈富琴,周渊平.不同信号的DOA估计算法比较[J].微型机与应用,2017,36(10):61-64,69.
0引言
近年来,用阵列信号处理技术实现对信号的波达方向(Direction of Arrival,DOA)估计成为了研究热点。DOA估计是在空域、时域谱估计的基础上发展来的一种技术,是阵列信号处理中的一个重要研究方向。DOA估计就是确定同时处在空间某一区域内多个感兴趣的信号的空间位置( 即多个信号到达阵列参考阵元的方向角)。DOA估计技术在近二十多年来得到了广泛的发展,并取得了大量的成果。
窄带信号的MUSIC算法利用的是接收数据协方差阵的噪声子空间的正交特性,而ESPRIT算法则是利用了数据协方差阵信号子空间的旋转不变性[1]。本文着重分析了MUSIC和 TLSESPRIT算法,然后在不同条件下对这两种算法的性能进行了 MATLAB的仿真和分析。窄带信号的频率相对不变,故阵列流型依赖于信源方位角 ,因此从时域的快拍数即可进行DOA估计,而信源为宽带信号时,阵列流型矩阵依赖于频率和角度,故需要在频域构建多个窄带模型,进而利用窄带DOA估计的方法进行处理。ISM算法是最早出现的宽带DOA估计算法,该方法在高信噪比时简单有效,然而在低信噪比时,由于某些频段上的DOA估计效果非常差,导致整体性能较差,但是能量加权法(EWISM)和能量门限法(ETISM)两种改进算法有效地改善了ISM算法存在的不足[2]。
1MUSIC算法模型
对于远场信号,波阵面考虑为平面波,在此假设信源为点源, 空间中有D个窄带的远场信号辐射到以均匀线阵上,阵元个数为M,阵元间距为d,阵元接收信号为nm(t),m=1,2,…,M(噪声互不相干且与信号不相干)。互不相关的信源信号为Sk(t),k=1,2,…,D。
信号可用如下的复包络形式表示:
Xm(t)=∑Dk=1sk(t)e-j2π(m-1)dλsinθk+nm(t)(1)
写成矩阵为形式为:
X(t)=AS(t)+N(t)(2)
求出接收矩阵的相关矩阵:
R=E{X(t)XH(t)}=APAH+σ2I(3)
其中,P=E{S(t)S(t)H},σ2为噪声功率 。
对式(3)中的协方差矩阵R求其特征值和特征向量。
在理想的条件下,协方差矩阵R的最小特征值为噪声方差σ2,且其重数为MD,即有:
λD+1=…=λM=σ2(4)
根据式(9)可以知道信号源的数目(其中K为R最小特征值的重数) :
D=M-K(5)
所以,M阵元可估计的最大信源数为:
Dmax=M-1(6)
矩阵的特征向量相互正交,因为最小特征值为噪声的贡献,所以其对应的那些特征向量构成噪声子空间,剩余的特征向量构成信号子空间,且信号子空间与噪声子空间相互垂直。
在信号源所在的方向上,方向向量a(θk)⊥ΩN(θk),k=1,2,…,D,处于信号子空间ΩS中,所以有:a(θk)⊥ΩN,构造矩阵:
En=[υD+1,…,υM](7)
则有:En⊥a(θk)=0,k=1,2,…,D
根据式(7)可以求得空间谱,搜索空间谱的最大值,即为入射方向。
2ESPRIT算法模型
以均匀线阵为研究背景,信号位于远场,从而在均匀各向同性的介质中到达阵列的是平面波。假设加性噪声在所有天线单元上都存在,而且是平稳零均值随机过程。将阵列描述为由两个子阵构成,这两个子阵在各方面都是相同的,只是彼此有一个已知的位移矢量的偏移。
ESPRIT算法的基本思想是:研究由阵列的位移不变特性而引起的信号子空间的旋转不变性,信号子空间是由数据矩阵X和Y张成的,均张成了维数为K的信号子空间,即矩阵A的列向量张成的空间,但Y张成的信号子空间旋转了一个相位[3]。
LSESPRIT 普通最小二乘的基本思想是用一个范数平方为最小扰动去干扰信号子空间,其目的是校正信号子空间中存在的噪声。
TLSESPRIT总体最小二乘的基本思想是同时扰动信号子空间和噪声子空间,并使扰动范数的平方保持最小。
ESPRIT算法的流程图如图1所示。

3TLSESPRIT与MUSIC对比实验
实验中,对信号DOA估计采用方差来衡量性能,并认为估计角度误差在2°范围内都是正确的估计。
(1)不同SNR下两种算法的对比
仿真条件:均匀线阵阵元数目M=8;一个信号源,快拍数N=100,入射角度DOA=10°,不同SNR下进行100次蒙特卡洛仿真,准确度及估计方差如图2所示。

由图2可知, 随着SNR的增加,两种算法DOA估计方差在减小,MUSIC算法DOA估计性能优于TLSESPRIT算法,方差更小,正确率更高。
(2)不同快拍数N下两种算法的比较
仿真条件:均匀线阵阵元数目M=8;一个信号源,SNR=0 dB,入射角度DOA=10°,不同快拍数下进行100次蒙特卡洛仿真,仿真结果如图3所示。

由图3可以看出随着快拍数的增加,两种算法DOA估计的方差在减小,MUSIC算法DOA估计性能优于TLSESPRIT算法,方差更小,正确率更高。
(3)不同入射角度下两种算法的比较
仿真条件:均匀线阵阵元数目M=8;一个信号源,快拍数N=100,SNR=0 dB,不同入射角度下进行100次蒙特卡洛仿真,如图4所示。
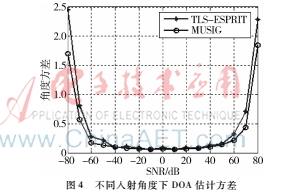
由图4可知,入射角度在-60°~60°的角度范围内DOA估计方差小,角度越靠近90°,DOA估计性能越差。
(4)两个信源时DOA估计结果直方图
仿真条件:均匀线阵阵元数目M=8;一个信号源,快拍数N=100,SNR=0 dB,入射角度DOA=[10,20],进行100次蒙特卡洛仿真,得到直方图如图5所示,DOA估计结果如表1所示。

由图5可知, MUSIC算法具有更高的分辨力,方差更小,性能更优。
4宽带信号ISM算法
对于窄带信号,其频率为常量,而宽带信号包含了大量的频点,频率是变量,当信号变为宽带信号时,阵列的流型矩阵A会发生变化。
第m个阵元在采样时刻t的输出为:
Xm(t)=∑Di=1si(t-τmi)+nm(t)(8)
其中,τmi表示第m个阵元对第i个信号相对于参考阵元的延迟。
对式(8)通过DFT变换到频域:
Xm(f)=∑Di=1Si(f)e-j2πfτmi+Nm(f)(9)
则阵列接收数据的频域矩阵表示形式如下:
X(f)=A(f,θ)S(f)+N(f)(10)
其中X(f),S(f),N(f)分别是阵列接收数据、信号、噪声经DFT变换后的频域数据:
A(f,θ)=[a1(f,θ),a2(f,θ),…,aD(f,θ)]
ai(f,θ)=[e-j2πfτ1i,e-j2πfτ2i,…,e-j2πfτMi]T
(1)EW-ISM算法
宽带信号在各个频率成分上的能量分布不均,ISM算法对于信噪比较低的频率点,进行估计的精度低,效果差,用以平均空间谱函数会使得估计误差增大。采用改进的EWISM算法对能量小的频点赋予小的权重,对能量大的频点赋予大的权重,最后对所有频点进行加权平均得到最终的空间谱[4]。
(2)ETISM算法
ISM算法由于在每个频点都需要进行DOA估计,因此,算法的计算量很大,实时性不好。ETISM算法是先求出各个子带上的能量值,然后设定一个合适的能力门限,若某一子带的能量大于该门限,则对其进行窄带空间谱处理,反之,则不予考虑。例如,以所有子带能量的均值为门限[5]。
4.1ISM算法DOA估计仿真实验
实验条件:两个线性调频信号,频率范围分别为:0~100 Hz,100~200 Hz,SNR=[10,10],阵元数M=8,阵元间距为最高频率对应半波长,划分子带数目:J=64,频域快拍K=32; DOA=[0,20],采用ISM算法,仿真结果如图6所示。

由图6可以看出,不同子带得到的空间谱效果不同,少数子带得到的空间谱中有两个谱峰,很多子带仅有一个谱峰,这是因为两个宽带信号频率基本无重叠,在100 Hz频率附近,含有两个信号的频率成分,这些子带能较准确地估计出两个谱峰,而远离100 Hz频率处的子带,仅包含一个信号的频率成分,故得到的空间谱中仅有一个谱峰。
4.2ISM与EWISM算法的比较
实验条件:同上,采用EWISM算法进行DOA估计,得到每个子带的空间谱和加权后的空间谱如图7所示。
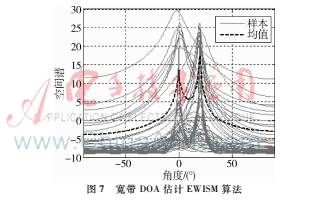
EWISM对不同子带的DOA估计结果进行了不同的加权处理,信噪比越高的子带权重越高,信噪比越低的子带权重越低,得到的空间谱的分辨力更高,估计结果更准确,如图7所示,经过加权后的EWISM算法优于传统的ISM算法。
4.3ETISM算法的仿真及分析
实验条件:同上,采用ETISM算法进行DOA估计,其中能量门限选择为个子带能量的均值,实验结果如图8所示。
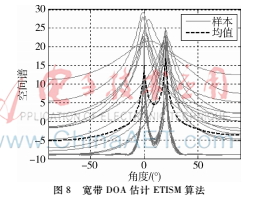
ETISM算法通过对子带进行筛选,选出了信噪比较高的子带进行DOA估计,舍弃了信噪比低的那些子带,减少了计算量,提高了DOA估计的精度。
4.4三种算法对不同宽带信号DOA估计
选择两组不同的宽带信号,一组信号频谱无重叠,另一组信号频谱部分重叠。
(1)频谱无重叠
实验条件:两线性调频信号频谱: 0~100 Hz,400~500 Hz;阵元数M=8, SNR=[10,10],阵元间距为最高频率对应半波长,信号为两个线性调频信号,划分子带数目J=64,频域快拍K=32; DOA=[0, 20];仿真结果如图9所示。
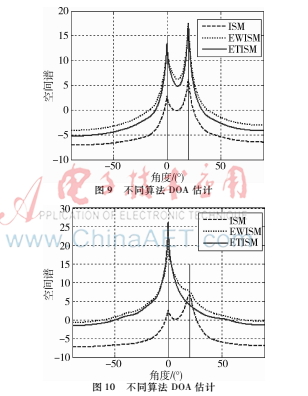
(2)信号频谱无重叠,信号功率差距大
实验条件:信号频率范围分别为:0~50 Hz,100~600 Hz,信噪比SNR=[20,10],其他条件同上,采用三种算法进行DOA估计,结果如图10所示。
(3)信号频谱部分重叠
实验条件:信号频率范围分别为:100~400 Hz,200~500 Hz,SNR=[10,10],其他条件同上,采用三种算法进行DOA估计,结果如图11所示。
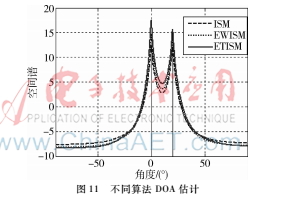
由图9~图11可以看出,当两信号频率成分重合较多时,三种算法性能基本相同。当信号频率无重叠且两信号信噪比相当时,部分子带不包含有用信号频率,这些子带DOA估计性能极差,若采用统计平均,将会影响整体性能。此时EWISM、ETISM有效地处理了上述问题,给予较小的权重或舍去相应的子带,效果较好。EWISM、ETISM算法优于传统的ISM算法,当两信号频谱无重叠且功率差距较大时,如图10所示,由于信号1功率大,信号2功率小,EWISM对信号1的子带加权大,对信号2子带加权小,此时DOA估计结果偏向信号1,信号2几乎被掩盖。同样,对ETISM算法,信号1的子带被选出,信号2的子带
被忽略,最终导致信号2处无法形成较好的谱峰,导致各算法性能均不理想,EWISM、ETISM算法均只有一个明显的谱峰,不如传统的ISM算法。为解决上述问题,可利用信号频带不同的特点,先对接收数据进行滤波处理,分别对滤波得到的信号进行单信源的宽带DOA估计,最终联合得到DOA估计结果。
5总结
与MUSIC算法相比,ESPRIT算法进行DOA估计同样具有较高的分辨力,而且不需要进行谱峰搜索,其计算量大大减小,但其估计精度不如MUSIC算法。由窄带信号的MUSIC算法引出了对宽带信号的处理,针对ISM算法的运算量大和精确度低两点不足,提出了EWISM、ETISM两种改进算法,两种算法克服了低信噪比子带对DOA估计结果的影响,仿真实验证明了该方法的有效性。通过对不同带宽的宽带信号DOA估计仿真实验,分析了各算法的不同应用场合:在两信号频谱有重叠且功率相当时,改进的两种算法要明显优于传统的ISM算法;而当其频谱无重叠时,若信号功率相当,则ETISM、EWISM明显优于ISM算法,若信号功率差距较大,此时三种方法效果都不理想,改进的算法可能不如传统的ISM算法,此时,可利用频带不重叠的特点进行滤波处理,对单个宽带信号作DOA估计,最终联合得到波达方向[6]。
参考文献
[1] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas & Propagation,1986,34(3):276-280.
[2] 王永良,陈辉,彭万宁,等.空间谱估计理论与算法研究[M].北京:清华大学出版社,2004.
[3] 张揽月,杨德森.矢量阵的非空间ESPRIT算法[J].哈尔滨工程大学学报,2009,30(4):406-410.
[4] 林静然,彭启棕,邵怀综,等.一种基于能量加权的阵列宽带信号定位算法[J]. 仪器仪表学报,2005,26(8):123-125.
[5] 司伟建,林晴晴.基于延时相关处理ESPRIT算法[J].系统工程与电子技术,2012,34(3):144-146.
[6] 刘庆华,伊晓东.基于分布式任意阵列的宽带信源定位方法研究[J].电子技术应用,2016,42(1):82-86.

