0 引言

    在数据挖掘、图像分类、目标识别等领域，经常需要对不同的数据进行分类。常用的策略是，先对已有的数据和先验知识进行学习并构造一个分类器，然后再采用分类器对待分类数据进行分类。分类器也可以看作是一个数据映射函数，可以将待分类数据映射到数据库中的某一个给定的类别^[1-3]。通常，数据分类方法统称为分类器。目前，常用的分类器有五类：(1)朴素贝叶斯分类器，该分类器具有收敛速度快的优点，对样本数量要求不高，可以适用于小样本的学习。但是，该分类假设数据条件独立，难以有效学习数据之间的关联信息^[4]；(2)逻辑回归分类器，该分类器的最大优点是支持增量学习，当分类器构建完毕之后，后续如果又有了新样本需要学习，可以采用在线梯度下降方法在原有分类器的基础上快速学习新的数据，而且，该分类器的正则化模型较多，不要求数据之间相互独立，但是该分类器的分类性能目前表现还不是很突出^[5]；(3)决策树分类器，该分类器首先需要构建一个属性集合，决策树基于属性集合来做出一系列的决策，实现数据的分类。该分类器易于处理数据间的关联信息，不限制数据是否异常或者线性可分。缺点是容易发生过拟合现象^[6]；(4)神经网络分类器，该分类器也对输入数据没有严格的要求，网络的构建比较灵活，但涉及参数较多，运算效率偏低^[7]；(5)支持向量机（Support Vector Machine，SVM）分类器，该分类器为过拟合提供了好的理论保证，泛化能力较强，对于小样本的学习尤其有效，分类效果较好。该分类器在学习非线性可分数据时，需要先将数据映射到高维空间，使得高维空间的数据线性可分。常采用核函数来完成数据由低维到高维的映射^[8]。然而，当数据维数较高时，核变换的复杂度较高，导致SVM的运算效率偏低。

    为了提高SVM分类器的运算效率，本文提出一种结合本征分解和抽样学习改进的快速SVM分类器，通过本征分解方法来降低低维空间向高维空间变换时核矩阵的维数，通过对训练样本进行抽样学习来降低数据处理量，提高SVM分类器的运算效率。

1 SVM概述

    SVM是一种应用广泛的分类器，基于结构风险最小原理进行学习，具有泛化能力强的优点，可以有效解决小样本的学习难题，在高维特征分类领域也有优势。

    依据训练数据的不同，可以将SVM分为线性SVM和非线性SVM两类，下面进行简要介绍。

1.1 线性SVM

    当训练数据线性可分时，可以采用线性SVM学习一个最优的分类面来进行分类。SVM的基本原理是：最优分类面既要能将两类样本正确分开，又要使得分类间隔最大。

    SVM的学习可以看作一个最优化问题，可以表示为：

1.2 非线性SVM

    当训练数据线性不可分时，可以采用非线性SVM学习一个最优分类面。通常的解决方法是：采用一个非线性的映射函数将低维空间上线性不可分的数据映射到高维空间上，变成线性可分的数据。依据Hilbert-Schmidt原理，满足Mercer条件的核函数可以代替高维空间上的点积运算。因此，这里的关键是选择一个合适的核函数来进行数据映射。核函数可以表示为：

其中，f(·)表示映射函数，用于表示将低维空间上的数据映射到高维的核空间F上。可见，核函数k(x_i，x_j)可以用高维空间上数据的乘积运算来代替低维空间上数据的点积运算。

    常用的核函数主要有3个，包括：

    (1)径向基函数(Radial Basis Function，RBF)，可以表示为：

2 改进的非线性SVM

    数据的核变换可以构建一个核矩阵K∈R^N×N，表示为：

其中，F是指数据x映射到核空间F上的数据集，可以表示为：

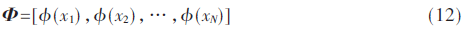
    当数据维数较高时，核变换的运算效率偏低。为了提高核运算效率，本文考虑对核矩阵进行降维处理。考虑到核矩阵K为正半定矩阵，通常可以通过本征分解来进行降维。因此，对于核空间F上的数据集F，可以分解为：

其中，L是由矩阵F的特征值构建的对角矩阵。这里，特征值按照从大到小的顺序降序排列。U为对应的特征向量矩阵。

    这样，低维空间上的数据x映射到高维空间之后对应的n维向量可以表示为：

    计算整个核矩阵仍然非常耗时，为了进一步提高运算效率，本文对训练子集进行划分，随机挑选包含n个训练样本的子集来计算K的子矩阵，表示为：

3 实验与分析

    分类器在图像分类领域应用非常普遍，因此，本节通过图像分类实验来测试和评价本文所述的改进SVM分类器的性能。

3.1 图像分类实验流程

    图像分类的基本流程如图1所示。主要包括两个阶段：(1)分类器训练阶段，主要是对训练数据集进行特征提取，依据先验的图像类别标签来进行分类器的训练；(2)图像分类阶段，对于待分类的图像，先要提取图像特征，然后结合训练阶段得到的分类器估计特征所属的类别，得到图像分类结果。

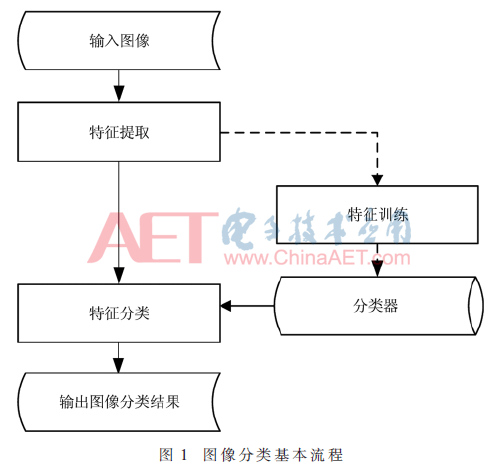
    其中，特征提取和特征分类是图像分类的关键环节。特征提取是对图像的抽象描述，常用的特征有Haar^[9]、方向梯度直方图（Histogram of Oriented Gradient，HOG）^[10]、局部二元模式（Local Binary Pattern，LBP）^[11]和尺度不变特征转换(Scale-Invariant Feature Transform，SIFT)^[12]等，本文将在后续实验中对不同的特征进行定量评测，进而选择最有效的特征进行图像分类。特征分类是本文的研究重点，本文所述方法是一种改进的SVM分类器，因此后续实验着重是将本文改进的SVM分类器与经典SVM分类器以及目前常用的一些分类器进行性能对比，具体将在后续实验部分详述。

3.2 实验数据集

    图像分类领域的公开测试的数据集比较多，本文选用目前常用的两个测试数据集，分别是PASCAL VOC-2007和COIL-100数据集，简要介绍如下。

    (1)PASCAL VOC-2007数据集

    该数据集包含20个类别的目标图像，这些目标存在尺度、视角和光照方面的变化，数据集包含的图像总数为9 963幅，其中训练子集中包含图像5 011幅，测试子集中包含图像4 592幅。

    (2)COIL-100数据集

    该数据集包含100个类别的目标图像，目标也存在尺度、视角及光照方面的变化，图像数量为7 200幅，其中训练子集中包含图像800幅，测试子集中包含图像6 400幅。

    后续对比不同的特征提取和分类方法时，分别在上述两个数据集上进行训练和测试，在相同的训练数据集和测试数据集上统计各种方法的性能指标，以便于验证本文方法的性能。

3.3 性能评价指标

    本文实验的目的主要用于评价改进SVM分类器的分类正确率和运算效率。因此，这里的图像分类实验选用3个性能评价指标，分别是分类正确率、训练耗时和平均分类耗时。其中，分类正确率可以用分类正确的图像总数与测试数据集中的图像总数的比值来表示，记为A_R。训练耗时指两个数据集的整个训练过程所耗费的总时间，记为T_T。平均分类耗时可以用所有测试图像的分类耗时与图像数量的比值来表示，记为T_C。需要说明的是：分类耗时与计算机平台性能有关。实验时不同方法使用相同的计算机平台进行测试。所有计算机平台的性能参数为：3.2 GHz四核 Intel I5 CPU、16G DDR3内存、Windows 7 32位操作系统、Visual Studio 2010开发环境。

3.4 实验结果与对比分析

3.4.1 特征选择对比

    下面首先对比采用不同特征时两个数据集的图像征分类性能指标，其中，图2展示了分别采用Haar、HOG、LBP和SIFT 4种特征时的图像分类结果，分类器采用的是本文改进的SVM分类器。其中，改进SVM分类器所用的核函数为径向基函数，参数σ取值为0.5。

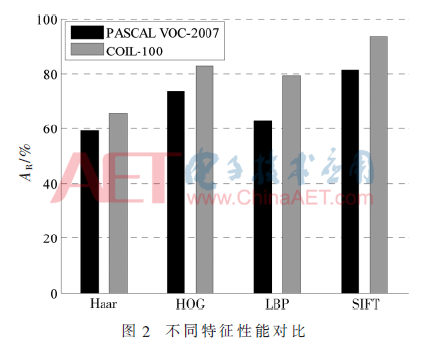
    由图2可见，在分类器相同的条件下，采用SIFT特征在两个数据集上测试所得的图像分类正确率指标都高于其他3种特征。这说明SIFT特征优于其他3种特征，因此，后续的实验中在特征提取阶段都采用SIFT特征对图像进行描述。

3.4.2 核函数选择对比

    本文1.2节列出了3种常用的核函数，分别是径向基函数（RBF）、二层神经网络函数（Sigmoid）和多项式函数（Polynomial）。采用的核函数不同，所得到的图像分类结果也不同。图3展示了分别采用3种不同的核函数时得到的图像分类正确率指标，其中，图3(a)采用的是经典的SVM分类器，详见文献[8]；图3(b)采用的是本文改进的SVM分类器。

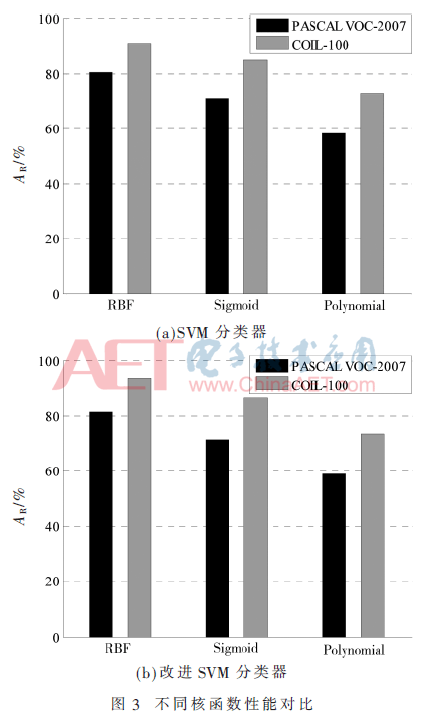
    由图3(a)和图3(b)可见，对于两个不同的数据集，不论是采用经典的SVM分类器还是采用本文改进的SVM分类器，都可以看出采用径向基函数作为核函数得到的图像分类正确率指标高于其他两种核函数，因此，后续实验中经典SVM分类器和本文改进的SVM分类器都选择径向基函数作为核函数。

3.4.3 分类器对比

    为了验证本文改进的SVM分类器的性能，下面采用不同的分类器进行对比实验。图4展示了分别采用经典SVM分类器、随机森林分类器、神经网络分类器和本文改进的SVM分类器得到的图像分类正确率指标。表1展示了对应的平均分类耗时指标。

    由图4可见，本文改进的SVM分类器得到的图像分类正确率指标略高于经典的SVM分类器，明显高于随机森林和神经网络分类器。这说明，相对于随机森林和神经网络分类器，SVM分类器的泛化能力更强，更适用于图像分类。同时，改进的SVM采用本征分解降低了噪声干扰，相对于经典SVM分类器其图像分类正确率指标略有提升。由表1可见，本文改进的SVM分类器的训练耗时明显低于其他3种分类器，平均分类耗时也明显低于经典SVM分类器和神经网络分类器，略高于随机森林分类器。这说明，通过降维和抽样处理，可以明显提高SVM分类器的分类耗时。因此，综合评价，本文改进的SVM分类器不仅提高了运算效率，而且提高了分类正确率。

4 结束语

    为了提高经典支持向量机分类器的运算效率，本文提出了一种结合本征分解和抽样学习改进的快速SVM分类器。主要是针对低维空间向高维空间变换时核矩阵运算效率低的问题进行改进：对核矩阵进行降维处理，采用本征分解方法得到核矩阵的近似表示，提高核矩阵的运算效率；在表示低维的核矩阵时，采用抽样学习的思想，先对训练数据进行划分，随机抽样一个数量很小的训练样本子集进行学习，进一步降低了数据量，进而提高了SVM分类器的运算效率。

    经过优化，不仅提高了SVM分类器的运算效率，也进一步强化了SVM分类器的泛化能力。通过将改进的SVM分类器与经典的SVM分类器以及常用的随机森林、神经网络分类器进行图像分类对比实验，证明了改进的SVM分类器不仅分类正确率高于经典SVM、随机森林和神经网络分类器，而且训练耗时最少，平均分类耗时也优于经典SVM分类器，是一种快速可靠的分类器。

参考文献

[1] LIU Q.Kernel local sparse representation based classifier[J].Neural Processing Letters，2016，43(1)：123-137.

[2] 杨春，殷绪成，郝红卫，等.基于差异性的分类器集成：有效性分析及优化集成[J].自动化学报，2014，40(4)：660-674.

[3] LIAN C，SU R，DEN?覹UX T.An evidential classifier based on feature selection and two-step classification strategy[J].Pattern Recognition，2015，48(7)：2318-2327.

[4] 王双成，高瑞，杜瑞杰.基于高斯核函数的朴素贝叶斯分类器依赖扩展[J].控制与决策，2015，30(12)：2280-2284.

[5] 郭华平，董亚东，邬长安，等.面向类不平衡的逻辑回归方法[J].模式识别与人工智能，2015，28(8)：686-693. 

[6] PUISSANT A，ROUGIER S，STUMPF A.Object-oriented mapping of urban trees using Random Forest classifiers[J].International Journal of Applied Earth Observation & Geoinformation，2014，26(1)：235-245.

[7] SUJAY R N，DEKA P C.Support vector machine applications in the field of hydrology：A review[J].Applied Soft Computing，2014，19(6)：372-386.

[8] CHAI R，LING S H，HUNTER G P，et al.Brain-computer interface classifier for wheelchair commands using neural network with fuzzy particle swarm optimization[J].IEEE Journal of Biomedical & Health Informatics，2014，18(5)：1614-1624.

[9] Chang Zheng，Ban Xiaojuan，Wang Yu.Fatigue driving detection based on Haar feature and extreme learning machine[J].Journal of China Universities of Posts & Telecommunications，2016，23(4)：91-100.

[10] YANG X, DI T.Research on mean-shift target tracking based on image HOG feature[J].Open Automation & Control Systems Journal，2015，7(1)：1022-1028.

[11] CIOCCA G，CUSANO C，SCHETTINI R.Image orientation detection using LBP-based features and logistic regression[J].Multimedia Tools and Applications，2015，74(9)：3013-3034.

[12] GHOUALMI L，CHIKHI S，DRAA A.A SIFT-based feature level fusion of iris and ear biometrics[C].Multimodal Pattern Recognition of Social Signals in Human-Computer-Interaction(MPRSS 2014)，2014：102-112.

作者信息：

武海燕1，李卫平1，2

（1.铁道警察学院 公安技术系，河南 郑州450000；2.武汉理工大学 信息工程学院，湖北 武汉430070）