文献标识码: A
DOI:10.16157/j.issn.0258-7998.171111
中文引用格式: 蒋从元,杨杰. 基于分布式多跳误差估计目标位置感知算法[J].电子技术应用,2017,43(11):95-98.
英文引用格式: Jiang Congyuan,Yang Jie. Energy efficiency target position aware algorithm with distributed multi-hop error estimates[J].Application of Electronic Technique,2017,43(11):95-98.
0 引言
在无线传感器网络定位算法[1-6]的研究上,谭志等[7]提出一种基于节点间覆盖关系的改进DV-Hop算法,该方法根据两节点间的通信覆盖率引入跳数系数,降低了每跳距离产生的误差,在一定程度上降低了DV-hop算法的定位误差。赵雁航等[8]提出一种基于跳距修正粒子群优化的WSN 定位算法,该算法通过对锚节点广播的数据分组结构进行了改进,来对定位误差进行加权处理并对定位的迭代过程进行优化,提高了无线传感器网络的定位精度。吴玉成等[9]提出一种基于最优节点通信半径的改进DV-Hop定位算法,该算法通过分析网络节点分布特性得到最优节点通信半径,并获得受扰动影响最小的锚节点优化分布方案,采用加权方法修正未知节点位置,改善了节点随机分布的无线传感器网络的节点定位性能。朱敏等[10]提出一种基于DV-HOP改进的无线传感器网络定位算法,该算法采用新的方式计算未知节点与锚节点的距离,提出锚节点信任度的概念,并利用加权最小二乘法计算节点坐标。该方法在提高定位精度的同时,减少了节点的通信量和计算量。JIANG K等[11]提出一种基于最小二乘法和DV-Hop算法的无线传感器网络的目标定位算法,移动信标节点引入DV-Hop,允许在预先安排的方式下移动信标节点,并连续广播其位置信息,形成多个虚拟信标。该算法可以减少网络的定位成本和复杂性。ZHANG Q G等[12]提出一种基于改进粒子群优化算法的无线传感器网络节点定位算法,通过将DV-Hop算法和简单的粒子群优化(tsPSO)算法结合在一起,该算法迭代地搜索未知节点,抑制对定位精度的距离估计误差,可以实现比DV-Hop算法更高的定位精度[13-15]。
1 NFDV-Hop定位算法
为了减少计算中的传播误差和提高定位精度,通过划分最接近锚节点的距离方程,未知节点再通过从方程组利用获得的信息更新位置信息。步骤如下:
(1)在这个步骤中,每个锚节点广播信标包与它的位置(坐标)并且跳数的值初始化为1。当节点接收到信标数据包,将生成一个表(xi,yi,n(hop)),这个表代表着节点所接收到的每个锚节点的位置坐标以及跳数信息。如果接收到的数据包中关于达到一个特定的锚节点是包含较少的跳数值,则表中的跳数值被替换为收到的数据包的跳数值,并且在网络中如果数据包被转发,则跳数值增加1,否则该数据包将被丢弃。通过这种机制,网络中的所有未知节点从每个锚节点获得锚节点的坐标和最小的跳数值。
(2)未知节点从步骤(1)中获得的锚节点的坐标后,未知节点计算锚节点跳数的大小,在这里假设节点的通信范围为R,用d(i,j)表示节点i到锚节点j的欧几里得距离,由于节点的跳距离是一定小于其通信距离,因此节点到锚节点所需的最小跳数为:

计算跳数后,未知节点使用跳数和锚节点之间的信息距离计算出锚节点的跳距离。为了使跳距离更加接近于实际跳距离的大小,未知节点采取锚节点之间的平均距离之比以及平均跳数来计算跳距离,得到:

而锚节点每一跳所产生的误差,则与跳数以及锚节点i与锚节点j之间的距离有关:

一旦未知节点计算平均跳数的大小,则开始通过使用平均跳距离和各自的锚节点的最小跳数来估计与锚节点的距离,未知节点估计与第i个锚节点的距离为:

通过每一次的距离划分来得到最接近锚节点真实距离的距离方程,假设第j个锚节点是最接近未知节点的锚节点i,首先得到距离的划分方程为:


2 实验仿真及分析
在仿真实验中主要进行定位误差和计算成本的分析,算法是在Matlab7.0仿真软件上进行编程和运行,在模拟的仿真环境中,包括了对100个随机生成的传感器节点部署,并且模拟的部署环境为一个面积为200×200的区域,每个节点都具有50 m的通信半径,在仿真中,定位误差定义为:

为了更好地验证本文所提出算法的性能,在实验中分别与文献[11]的基于最小二乘法的DV-Hop算法以及文献[12]的基于改进粒子群优化的DV-Hop算法进行了对比,并得到了仿真结果的比较图。
图1定位误差是衡量定位算法性能的关键,为了验证算法的定位误差情况,实验中在初始的节点数量的情况下增加节点数量,从初始的100个节点增加到300个,并得到在节点数量增加的过程中算法的定位误差情况。从图1的结果可以看出,节点数量越多,定位误差越小,这是由于节点数量增多后,节点间的距离计算的误差就相对减小,因此定位精度变高。从与基于最小二乘法的DV-Hop算法以及基于改进粒子群优化的DV-Hop算法的对比情况可以看出,本文方法的定位误差保持在27.5%以下,定位误差最低时仅为5.7%。而对比算法的定位误差最低时分别为17.8%和14.7%。因为基于最小二乘法的DV-Hop算法以及基于改进粒子群优化的DV-Hop算法都是专注于修改其估计平均跳距离,通过减小平均跳距离误差来提高未知节点距离的估算精度,再通过未知节点与锚节点的位置关系来实现坐标定位。然而平均跳距离作为估算距离始终存在一定的误差,因此提高精度的能力有限。而NFDV-Hop算法除了通过多个锚节点的平均距离之比以及各自的锚节点的最小跳数来提高的平均跳距离的估算精度,而且估计的跳距离采用距离的划分方程来得到未知节点的估计坐标,并引入位置比值来提高位置坐标的估算精度。

为了验证算法的节能性能,在实验中通过逐渐增加节点数量,得到网络的平均节点能耗情况。从图2的结果可以看出,本文的平均节点能耗相比对比算法少了很多,最高时仅为0.768 J,最低时为0.529 J,而两种对比算法的最低平均节点能耗则分别为0.754 J和0.696 J,因此相比之下本文算法的节能性能更加显著。

当锚节点在总的节点数量的占比增加时,意味着可以用来作为距离测量的锚节点数量增多,即定位精度会有一定提升。该组实验即在锚节点占比提升的情况下,验证算法的定位误差。从图3的结果可以看出,3种算法的定位误差都随着锚节点占比的提升而减少,定位精度有所提升。从曲线的分布情况来看,定位误差最低的为本文的NFDV-Hop定位算法,其次为改进粒子群优化的DV-Hop算法,而基于最小二乘法的DV-Hop算法的定位误差最高。
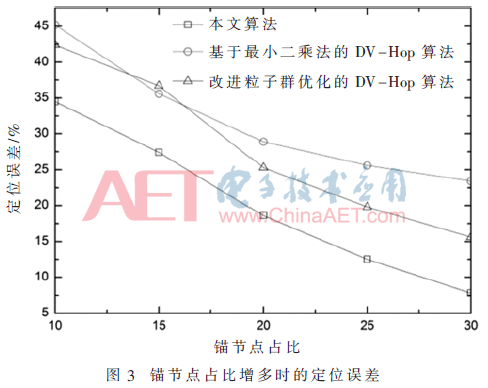
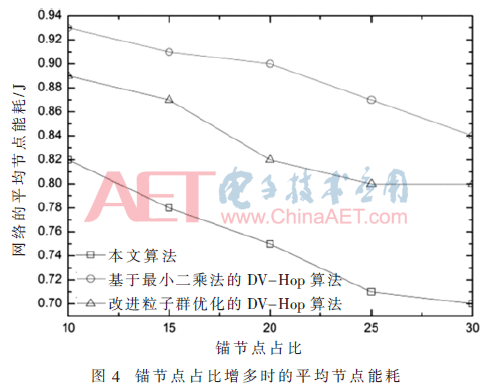
图4为锚节点在总的节点数量的占比增加时的平均节点能耗情况,由于本文算法的锚节点只需广播一次自身的位置信息,因此锚节点占比的提升,意味着节点的总的通信成本降低,即平均节点能耗也降低。因此在锚节点在总的节点数量的占比增加时,本文算法的平均节点能耗的降低趋势较为明显,而另外两种算法的能耗降低并不多,在锚节点占比为30%,本文算法的平均节点能耗为0.706 J,另外两种算法分别为0.842 J和0.805 J。因为基于最小二乘法的DV-Hop算法在广播消息上与DV-Hop算法相同,并没有起到节能效果,而基于改进粒子群优化的DV-Hop算法需要多次迭代,节能效果不理想。而NFDV-Hop定位算法专注于减小通信成本,通过有效减少信息的广播次数减少节点的能量消耗,从实验结果来看起到了一定的效果。
3 结论
本文提出了一种分布式多跳误差估计的能量高效目标位置锁定算法,该算法在DV-Hop算法的基础上,针对DV-Hop算法定位精度不高、通信成本较大的问题,采用节能非测距优化方法,锚节点只需广播一次自身位置坐标信息,有效减少通信能耗。使用锚节点的平均跳数的大小以及锚节点间的平均跳距离来求得未知节点的位置坐标。在实验中,通过验证和对比的方法来体现本文算法在减小定位误差和能量消耗上的有效性。
参考文献
[1] YU C B,YU L,TAN J,et al.DV-Hop localization algorithm in WSN based on weighted of correction in hop distance[J].Applied Mechanics and Materials,2013,303:143-148.
[2] GUO Z,MIN L,LI H,et al.Improved DV-Hop localization algorithm based on RSSI value and hop correction[M].Advances in Wireless Sensor Networks.Springer Berlin Heidelberg,2013:97-102.
[3] CHAO J,HAN G,ZHU C,et al.Performance evaluation of DV-hop localization algorithm with mobility models for Mobile Wireless Sensor Networks[C].Wireless Communications and Mobile Computing Conference(IWCMC),2013 9th International.IEEE,2013:1827-1832.
[4] HU Y,LI X.An improvement of DV-Hop localization algorithm for wireless sensor networks[J].Telecommunication Systems,2013,53(1):13-18.
[5] ZHANG J,WANG H B,QIAO X G,et al.Node localization algorithm based on DV-HOP in wireless sensor networks[J].Applied Mechanics and Materials,2014,440:289-292.
[6] KUMAR S,LOBIYAL D K.Improvement over DV-Hop localization algorithm for wireless sensor networks[J].World Academy of Sciences, Engineering and Technology,2013:282-292.
[7] 谭志,张卉.基于节点间覆盖关系的改进DV-Hop算法[J].北京邮电大学学报,2014,37(1):35-38.
[8] 赵雁航,钱志鸿,尚小航,等.基于跳距修正粒子群优化的WSN定位算法[J].通信学报,2013,34(9):105-114.
[9] 吴玉成,李江雯.基于最优节点通信半径的改进DV-Hop定位算法[J].华南理工大学学报(自然科学版),2012,40(6):36-41.
[10] 朱敏,刘昊霖,张志宏,等.一种基于DV-HOP改进的无线传感器网络定位算法[J].四川大学学报(工程科学版),2012,44(1):93-98.
[11] JIANG K,YAO L,FENG J.Wireless sensor networks target localization based on least square method and DV-Hop algorithm[J].Journal of Networks,2014,9(1):176-182.
[12] ZHANG Q G,CHENG M.A node localization algorithm for wireless sensor network based on improved particle swarm optimization[M].Mechatronics and Automatic Control Systems.Springer International Publishing,2014:135-144.
[13] CHANDRASEKHAR V,SEAH W K G,CHOO Y S,et al.Localization in underwater sensor networks:survey and challenges[C].Proceedings of the 1st ACM international workshop on Underwater networks.ACM,2006:33-40.
[14] LIN J Z,LIU H,LI G,et al.Study for improved DV-Hop localization algorithm in WSN[J].Application Research of Computers,2009,26(4):1272-1274.
[15] WANG Y,WANG X,WANG D,et al.Range-free localization using expected hop progress in wireless sensor networks[J].Parallel and Distributed Systems,IEEE Transactions on,2009,20(10):1540-1552.

