0 引言

    随着电子技术和互联网技术的迅速崛起，特别是云计算商业化平台的出现，不安全信道中消息认证变得越来越重要。在消息认证过程中，通常采用构造消息认证码(Message Authentication Code，MAC)的方式实现^[1]。该方法可有效地检测在传输过程中数据是否存在被篡改，目前已被广泛应用在数字签名、文件校验、流密钥产生等方面^[2]。针对MAC算法的安全性、效率和能耗等问题，许多学者已经对此开展深入的研究。刘云璐等^[3]提出一种消息认证协议优化算法，解决信息在树状传感器网络中的上层节点处拥堵和被丢弃的问题。王利村等^[4]提出一种采用固定帧长的EPONMAC算法，使以太网交换机的速率得以提升。卢艳宏等^[5]提出用于无线传感器网络数据传输的混合型消息认证算法，解决了能量损耗问题。但是，上述所提的方法均采用原始数据进行传输，存在消息被泄露的威胁。

    近年出现的全同态加密技术，它允许对密文执行特定的操作后将其输出进行解密，解密所得的结果与对明文进行相同操作的结果相等。全同态加密不但能够提高数据处理效率、确保数据安全传输，而且可以有效避免将原始数据委托给第三方操作的安全问题。但是怎样构造密码体制使其具有全同态性质是学术界面临的难题之一。2009年9月，GENTRY C等^[6]在ACM计算理论年会上对“全同态加密”的可行性从数学上进行了论证，并给出具体实现方案，即在不解密的条件下对密文数据进行运算与对明文进行相同运算后加密的结果相同。DIJK M等^[7]提出一种整数型全同态加密的优化方案，极大地简化电路的硬件结构。鉴此，本文针对数据传输的安全问题，提出一种基于全同态MAC的消息认证算法，在SMIC 65 nm工艺下完成硬件电路设计。实验结果表明，该结构不仅具有良好的黑盒性，还能够检验传输数据是否完整。

1 全同态算法和MAC算法

1.1 全同态算法

    在密码系统中，设m为明文，c为密文，Enc为加密操作，Dec为解密操作，则有c=Enc(m)，m=Dec(c)。在全同态算法中，设f为任意操作，则全同态过程可表示为Dec(f(Enc(m)))=f(m)或f(Enc(m))=Enc(f(m))。全同态算法主要包括密钥的生成、加密和解密3个阶段，具体如下所示：

    (1)密钥的生成。随机产生一个密钥p，且p为素数。

    (2)全同态加密。对任意的明文m加密可得密文c=m+2r+pq。其中p为正的奇数，q为较大的正整数(比p要大，是否是奇数没有要求)，r为加密时由$random函数产生的较小整数(没有正负要求)，m为明文(m∈{0，1})。全同态加密完成对1位二进制数的加密，所得结果是N位整数。

    (3)全同态解密。对任意的密文解密可得m=(c mod p)mod2。mod p表示以p为基数进行的模运算，可等效为以下运算：c mod p=c-「c/p」×p，其中「c/p」为c除以p的商取整。

1.2 MAC算法

    MAC算法作为一种可携带密钥的hash函数，通常用来检验所传输消息的完整性。常用的hash函数有MD5、SHA-2和SHA-3等，本文将采用MD5算法。MD5算法^[8]可将任意长度的消息或文本进行相关运算，使其压缩成128位固定长度的摘要，具体如下所示：

    (1)补位。任意长度消息的低位用一个1和若干个0进行补位，在结果后面添加消息的最初长度（用64位二进制数表示），使消息长度刚好成为512的整数倍。

    (2)初始化缓冲器。A₁，A₂，A₃，A₄是4个32位寄存器，也称作链接变量的整数参数，并对其设置初始数据。

    (3)非线性轮运算。声明四个中间变量a₁，a₂，a₃，a₄，对其进行赋值：a₁=A₁，a₂=A₂，a₃=A₃，a₄=A₄。接着执行4轮主循环，每一轮完成16次运算，每轮用到一个非线性函数；每次操作需要对a₁，a₂，a₃和a₄中的3个变量完成一次非线性运算，并更新对应的变量数据。四轮非线性函数分别如下所示：

    (4)数据输出。当64步运算完成之后，将a₁，a₂，a₃，a₄分别与初始的值分别进行相加，然后对下一组512位数据进行运算，最后得到的结果为4个32位数据级联构成的128位输出，即32位16进制的MD5码。

2 全同态MAC消息认证的VLSI实现

    消息认证是指对要传输的消息或者和消息相关的信息执行一系列操作后再进行认证，目的是为了防止消息在传输和存储过程中存在恶意篡改或错误修改，认证内容主要包含消息是否被篡改或延迟、消息是否来自真正的发送者等。图1为消息认证系统的结构框图。

2.1 全同态MAC的消息认证算法

    全同态MAC的消息认证算法通过对消息进行全同态加密操作，再采用MD5算法对加密后的数据进行扰乱处理，不但避免在通信信道中传输原始数据的安全问题，而且能够检测消息有没有被篡改，进而确保消息传输的可靠性。本文结合全同态算法和MD5算法，提出一种全同态MAC的消息认证算法，该算法的具体实现方案如下：

    步骤1：将算法中输入的二进制数据进行全同态加密处理得到密文。

    步骤2：通过步骤1处理后，将数据经过MAC算法，使其生成MAC₁值，将MAC₁值及密文在信道中传输。

    步骤3：接收方收到MAC₁值和密文后，运用相同的MAC算法对密文进行运算，生成MAC₂值，对比MAC₁值和MAC₂值，若一致，则用全同态解密算法对密文解密，恢复原始数据；若不一致，则接收方重新发送。

    全同态MAC算法流程图，如图2所示。整个过程消息一直以密文进行传输，保证了原始消息安全性，只有当接收方确认消息来源和完整性后才进行密文的解密。全同态MAC算法的伪代码，如图3所示。其中，fhe表示全同态加密模块，fhd表示全同态解密模块，top表示全同态MAC算法模块。

2.2 全同态MAC的消息认证算法硬件结构

    全同态MAC的消息认证算法的具体结构如图4所示。该算法首先执行全同态加密运算，将所得的结果经过数据控制模块用1和0进行补位，并以信息长度为512位进行分组。每个分组又被分成16个32位子集，每个子集用M_j（j为0到15）表示，以新变量和子集作为输入进行四轮主循环，每一轮循环需要完成16次迭代运算，其中每轮运算选择一个不重复的非线性函数。第一轮选择F(a₂，a₃，a₄)，则功能函数(a₁，a₂，a₃，a₄，M_j，g，t_i)可表示为FF(a₁，a₂，a₃，a₄，M_j，g，t_i)，代表含义为a₁=a₂+(a₁+(F(a₂，a₃，a₄)+M_j+t_i)<<<g)，其中<<<g表示循环左移g位。每进行一次迭代，根据功能函数更新a₁，a₂，a₃和a₄中的一个，通过16次迭代后，得到更新后a₁，a₂，a₃和a₄的数值。然后，将更新后的数值应用于第二轮循环，以此类推，完成四轮循环；其次，将此时的a₁，a₂，a₃和a₄的数值分别与原来的A₁，A₂，A₃，A₄相加；最后，对下一分组数据进行相同操作，当所有分组都完成运算后，将新的A₁，A₂，A₃，A₄按顺序级联成128位数据输出。

3 实验结果与分析

    采用SMIC 65 nm CMOS工艺，实现基于全同态MAC的消息认证算法硬件电路。实验环境包括Intel Xeon(R) Dual-Core CPU 2.0 GHz、6 G RAM服务器，涉及的工具软件包括：NCverilog仿真软件和DC综合工具。表1为p=11，q=121时，输入数据经过全同态加密模块的输出数据。表2为p=11，q=121时，输入数据经过全同态MAC算法的输出数据。

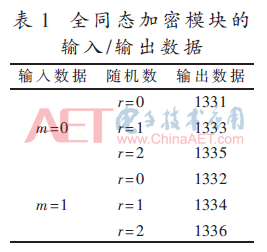
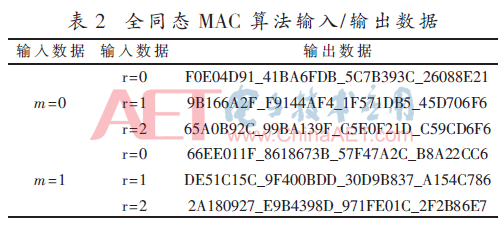
    图5为数据经过全同态MAC算法后输出数据之间的相关性。其中，图5（a）为同一组输出数据的自相关函数，图5（b）为6组测试数据之间的互相关函数。表明算法输出数据具有良好的随机特性。

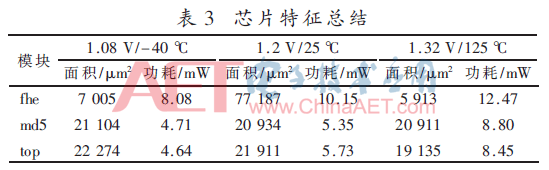
    不同温度/电压下DC综合的特征，如表3所示。其中，fhe为全同态加密模块，fhd为全同态解密模块，top为基于全同态MAC算法模块。在1.2 V电压下，DC综合后电路面积为219 11 μm²，工作频率最高可达到204 MHz，功耗为5.73 mW。

4 结论

    本文通过对全同态算法和MD5算法的研究，提出了一个全同态MAC的消息认证算法设计方法。将全同态加密生成数据与原有的结果进行比较，验证其黑盒性。实验结果表明，该算法有效避免在通信信道中传输原始数据的安全问题，同时可以检测消息是否被篡改，确保消息传输的可靠性。

参考文献

[1] 徐津，巧燕，王大印.一种基于Hash函数和分组密码的消息认证码[J].计算机学报，2015，38(4)：793-803.

[2] 张绍兰.几类密码Hash函数的设计与安全性分析[D].北京：北京邮电大学，2011.

[3] 刘云璐，蒲菊华，方维维，等.一种无线传感器网络MAC协议优化算法[J].计算机学报，2012，35(3)：529-839.

[4] 王利村，邱昆，王东，等.一种固定帧长的EPON MAC算法[J].电子科技大学学报，2004，33(6)：730-733.

[5] 卢艳宏，掌明，冯源.无线传感器网络能量高效混合MAC算法[J].电讯技术，2012，5(8)：1349-1353.

[6] GENTRY C.Fully homomorphic encryption using ideal lattice[C].Proceedings of the 41st Annual ACM Symposium on Theory of Computing，New York：ACM Press，2009：169-178.

[7] DIJK M，GENTRY C，HALEVI S，et al.Fully homomorphic encryption over the integery[C].Proceedings of EUROCRYPT’2010，Berlin：Springer，2010：24-43.

[8] 张裔智，赵毅，汤小斌.MD5算法研究[J].计算机科学，2008，35(7)：295-297.