文献标识码: A
DOI:10.16157/j.issn.0258-7998.172127
中文引用格式: 杨雪梅,徐家品,何希. 基于特征值对数分布的频谱感知算法[J].电子技术应用,2018,44(1):79-83.
英文引用格式: Yang Xuemei,Xu Jiapin,He Xi. Spectrum sensing algorithm based on the logarithmic distribution of eigenvalue[J]. Application of Electronic Technique,2018,44(1):79-83.
0 引言
在实际通信环境中,对于认知无线电(Cognitive Radio,CR)[1]的频谱感知,针对信号相关和噪声不确定现象很可能同时存在的问题,国内外学者们提出了许多有效的频谱感知方法[2-4],这些方法成功地规避了经典检测法的缺点。随着认知无线电技术的广泛发展与深入研究,基于随机矩阵理论(Random Matrix Theory,RMT)的频谱感知方法成为了研究热点[5-6]。文献[7]中利用了Wishart矩阵最大特征值的分布,将算术平均特征值近似为噪声的方差,得到了较高的检测性能,但在采样点数小、信噪比低时,性能略差;针对最小特征值的极限分布比最大特征值的极限分布更精确这一条件,文献[8]、[9]分别利用了最小特征值的一阶和二阶Tracy-Widom分布特性,通过减小判决门限来提高检测性能,但Tracy-Widom函数求解很困难,只能通过查表获得一些离散值;文献[10]、[11]中利用多元统计理论和协方差矩阵的分布特性,得到特征值表达式的对数分布形式,但在低信噪比条件下,需通过增加样本点来提高检测性能;文献[12]中利用了卡方分布和中心极限定理,推导出了算术平均特征值的分布特性,其中AME(Average to Maximum Eigenvalue)算法的检测性能要在较多协作用户数条件下才高于最大最小特征值算法[13]。
针对以上各算法的问题,本文运用接收信号的样本协方差矩阵几何平均特征值的对数分布规律特性,提出了一种基于样本协方差矩阵最大最小特征值之差与几何平均特征值(Difference between the Maximum-Minimum and Geometric mean eigenvalue,DMMG)比值的频谱感知算法,并对该算法的感知性能进行了理论分析和仿真验证。与其他算法相比,该算法检测性能较好,受样本中极端值和虚警概率的影响较小,且判决门限十分简单。
1 系统模型
1.1 多用户协作频谱感知场景
本文采用图1所示的认知无线电网络系统。该系统由多个主用户(Primary User,PU)、多个认知用户(Secondary User,SU)、一个主用户基站(Primary Base Station,PBS)和一个认知用户基站(Secondary Base Station,SBS)组成,PU通过PBS进行通信,SU通过多用户协作的方式对PBS发射的信号进行接收和采样,并将这些采样数据送到SBS中进行相应的处理,从而判断该段频谱是否空闲,实现多用户协作频谱感知。

1.2 频谱感知模型
SU通过对接收信号的检测来判断PU信号是否存在,用H1表示噪声与信号同时存在的情况,用H0表示只有噪声的情况,则整个检测过程可以建模为一个二元假设检测模型:


2 DMMG算法的理论分析
2.1 样本协方差矩阵的几何平均特征值特性
当PU信号不存在时(H0),则:

2.2 DMMG算法的判决门限推导


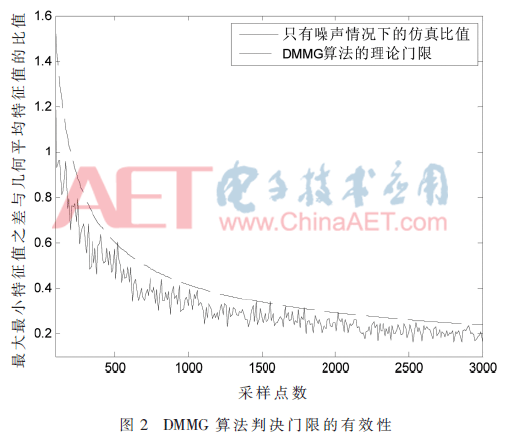
2.3 DMMG算法判决门限的有效性
由判决门限表达式(19)可知,γ只与采样点数N、协作用户数M和虚警概率Pfa有关。给定Pfa=0.01,M=10,进行仿真,如图2所示。由仿真结果可知,γ随采样点数的变化而动态调整;在不同采样点数情况下,γ的关系曲线位于只有噪声情况下的关系曲线的上方;由于存在虚警概率,在只有噪声情况下的值也可能存在极少的点位于γ关系曲线的上方。根据判决规则式(20)可知,仿真结果已验证DMMG算法判决门限的有效性。
3 算法性能仿真
3.1 仿真环境及工具
本文分别从不同信噪比、协作用户数、采样点数、虚警概率以及样本中存在极端值情况5个方面对DMMG算法进行仿真分析。在仿真中,DMMG算法将与AMME(Average to Maximum-Minimum Eigenvalue)、NMME(Novel Maximum-Minimum Eigenvalue)、AME以及BESD(Blind Eigenvalues Detection)算法进行比较;实验采用10 000次的Monte Carlo仿真,仿真平台为MATLAB(R2013a)。
3.2 仿真结果及分析
3.2.1 检测概率与信噪比的关系
各种算法在不同信噪比(dB)情况下的检测性能如图3所示。其中N=100,Pfa=0.05,M=5。由图可知,在低信噪比条件下,DMMG算法的检测性能高于其他4种算法,当SNR=-6 dB时,DMMG算法的检测概率已达0.954。当采样点数为100、虚警概率为0.05、协作用户数为5时,信噪比在-20 dB~-5 dB的范围内,DMMG算法的性能最好。

3.2.2 检测概率与协作用户数的关系
各种算法在不同协作用户数情况下的检测性能如图4所示,其中N=200,Pfa=0.05,SNR=-8 dB。由图可知,在小协作用户数情况下,DMMG算法的检测性能最佳。当M=5时,DMMG算法获得0.938的检测概率。在采样点数为200、虚警概率为0.05、信噪比为-8 dB时,协作用户数在3~6的范围内,DMMG算法的感知性能最优。

3.2.3 检测概率与采样点数之间的关系
各种算法在不同采样点数情况下的检测性能如图5所示,其中M=5,Pfa=0.05,SNR=-8 dB。由图可知,在相同采样点数情况下,检测概率最高的是DMMG算法;当N=200,DMMG算法已达0.933的检测概率,优于其他算法。在虚警概率为0.05、信噪比为-8 dB、协作用户数为5时,采样点数大于协作用户数并小于350的范围内,DMMG算法的感知性能最高。

3.2.4 样本中极端值对检测性能的影响
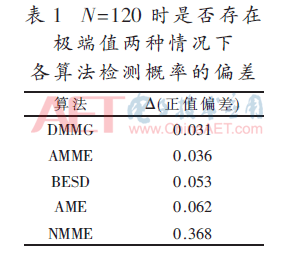
表1列出了当N=120时,各种算法在是否存在极端值两种情况下检测概率的偏差(取正值)。可见其中DMMG算法的偏差最小。
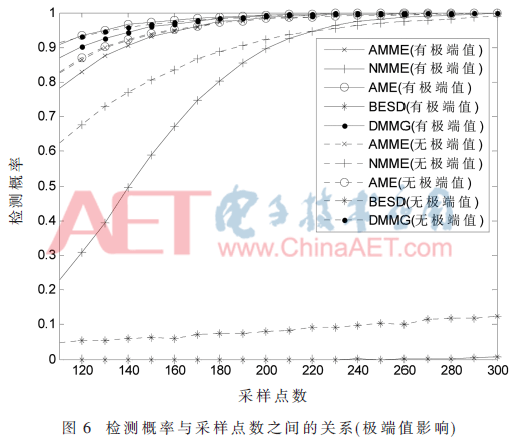
在是否存在极端值两种情况下各种算法的检测概率随采样点数变化的关系曲线如图6所示,其中M=10,Pfa=0.05,SNR=-10 dB。当样本中存在极端值时,BESD算法几乎完全丧失检测性能,NMME和AME两种算法的关系曲线与理想情况(无极端值)下存在较大的差异。DMMG算法在是否存在极端值两种情况下的仿真曲线均位于AMME算法关系曲线的上方。综上,DMMG算法受样本中极端值的影响较小,其检测性能优于其他4种算法。
3.2.5 检测概率与虚警概率的关系
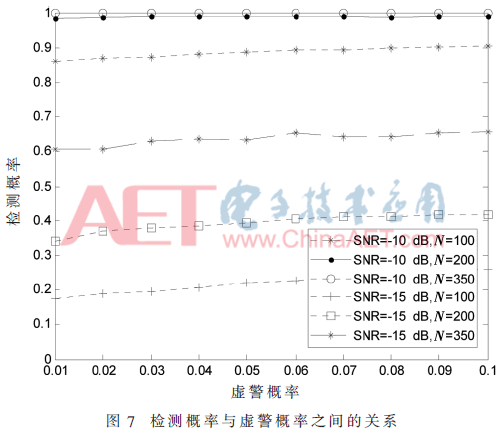
检测概率随虚警概率变化的关系曲线如图7所示,其中,M=10;采样点数N=100,200,350;信噪比SNR=-10 dB,-15 dB。结果表明,当虚警概率从0.01增加到0.1,在不同的采样点数和信噪比情况下,DMMG算法的检测概率增加均不到0.1。由此可知,DMMG算法受虚警概率的影响较小。
4 结论
本文运用特征值的对数分布特性,提出了一种基于接收信号样本协方差矩阵最大最小特征值之差与几何平均特征值比值的新算法,即DMMG算法。该算法不敏感于噪声不确定性,不依赖于Tracy-Widom定理,通过与AMME、NMME、AME和BESD 4种算法相比较可得:DMMG算法在低信噪比、低协作用户数以及低样本点数条件下,具有更好的检测性能,当满足协作用户数多于3少于6,采样点数大于协作用户数并小于350,信噪比在-20 dB~-5 dB的范围内,DMMG算法的感知性能达到最优。此外,DMMG算法的感知性能较为稳定,受虚警概率和样本中极端值的影响较小。
参考文献
[1] MITOLA J,MAGUIRE G Q.Cognitive radio:making software radios more personal[J].IEEE Personal Communications,1999,6(4):13-18.
[2] BENEDETTO F,GIUNTA G,RENFORS M.A spectrum sensing algorithm for constant modulus primary users signals[J].IEEE Communications Letters,2016,20(2):400-403.
[3] SIMPSON O,ABDULKADIR Y,SUN Y.Optimal entropy quantization for maximum likelihood estimation based cooperative spectrum sensing[C].IEEE Wireless Telecommunications Symposium(WTS),London,United Kingdom,2016:1-5.
[4] 曹开田,杨震.基于随机矩阵理论的DET合作频谱感知算法[J].电子与信息学报,2010,32(1):129-134.
[5] AHMED A,HU Y F,NORAS J M,et al. Random matrix theory based spectrum sensing for cognitive radio networks[C].Internet Technologies and Applications(ITA),Wrexham,2015:479-483.
[6] 刘宁,史浩山,刘利平,等.基于随机矩阵的新型频谱盲感知方法[J].西北工业大学学报,2016,34(2):262-267.
[7] 刘会衡,邓小鸿,陈伟.一种基于特征值的多天线认知无线电盲感知算法[J].计算机应用研究,2015,32(1):191-193.
[8] 弥寅,卢光跃.基于特征值极限分布的合作频谱感知算法[J].通信学报,2015,36(1):84-89.
[9] 杨智,徐家品.基于最小特征值分布的频谱感知算法[J].计算机应用,2015,35(2):354-357.
[10] LEI K J,YANG X,PENG S L,et al. Determinant of the sample covariance matrix based spectrum sensing algorithm for cognitive radio[C].IEEE Int Conf WiCOM,Wuhan,China,2011:1-4.
[11] 雷可君,杨喜,彭盛亮,等.基于特征值检测的多天线盲频谱感知算法的研究[J].系统仿真学报,2012,24(7):1549-1554.
[12] 徐家品,杨智.基于随机矩阵特征值比的频谱感知改进算法[J].电波科学学报,2015,30(2):282-288.
[13] ZENG Y H,LIANG Y C.Eigenvalue-based spectrum sensing algorithms for cognitive radio[J].IEEE Transactions on Communications,2009,57(6):1784-1793.
[14] BAO Z Q,HUANG Q D,ZHAI Y Z,et al.Fast blind spectrum sensing method based on determinant of covariance Matrix[C].IEEE Int Conf CSIP,Xi′an,Shaanxi,2012:439-443.
[15] MUIRHEAD R J.Aspects of multivariate statistical theory[M].Hoboken,NJ,USA:John Wiley&Sons,Inc,1982:85-101.
[16] BAI Z D.Methodologies in spectral analysis of large dimensional random matrices,a review[J].Statistica Sinica,1999,9(3):611-662.

