文献标识码: A
DOI:10.16157/j.issn.0258-7998.171559
中文引用格式: 白琼,张斌珍,段俊萍. W波段矩形波导滤波器的设计[J].电子技术应用,2018,44(2):66-69,74.
英文引用格式: Bai Qiong,Zhang Binzhen,Duan Junping. Design of W band rectangular waveguide filter[J]. Application of Electronic Technique,2018,44(2):66-69,74.
0 引言
随着现代通信技术的发展,对通信系统容量的需求逐渐增大。最近几年,由于低频波段和中频波段的迅速饱和,越来越多的人开始对高频波段尤其是W波段进行了相关的电磁研究[1]。W波段指的是频率从75 GHz~110 GHz的电磁信号,在此频率波段,波导器件的研究日益成熟。研究者们已经设计了一些工作于W波段的射频器件[2-4],具有一定的实用价值。
微波滤波器作为电磁通信系统中的重要组件,其性能好坏直接决定了电磁通信设备与系统的性能与价值。矩形波导因其低损耗、高功率容量等优点而被广泛应用于高频电磁通信系统中,并且其尺寸在毫米波频段甚至更高频段内随着频率的增大会急剧减小[5]。高频滤波器尺寸小,矩形波导结构简单且易于加工,因此高频矩形波导滤波器深受人们青睐。因此,开展滤波器尺寸参数与其性能指标(如总心频率、带宽、回波损耗、插入损耗、矩形系数等)之间的内在关系研究是必不可少的。
基于上述需求,本文设计了一款W波段矩形波导滤波器,并使用电磁仿真软件HFSS对其结构参数进行了参数优化与仿真,研究了滤波器的性能指标与其各个结构参数之间的内在关系,为矩形波导滤波器的设计提供了新的思路,也方便了滤波器的设计与仿真,有一定的实际意义。
1 结构设计
1.1 整体结构设计
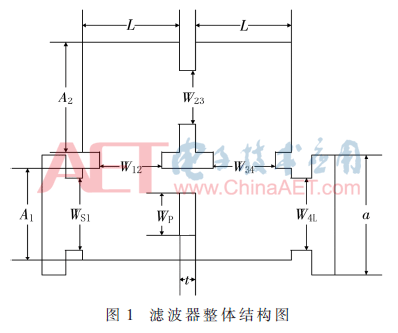
本文设计的滤波器模型整体结构及其相关参数如图1所示。滤波器四周封闭,仅保留输入与输出接口。考虑到滤波器的中心频率,滤波器的输入输出接口采用标准矩形波导端口WR-10(2.54 mm×1.27 mm)连接来实现信号的传输。为便与仿真与加工,滤波器整体结构高度与WR-10矩形波导口德高度保持一致。
1.2 交叉耦合结构
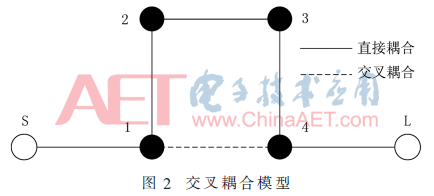
研究者已经提出了多种能实现相邻谐振腔之间能量交换的交叉耦合结构,例如CT结构、CQ结构等。交叉耦合结构的使用能在通带两侧各产生一个传输零点,提高带外抑制。CQ交叉耦合结构简单易仿真,且对本文设计的模型而言,便与加工实现。本文设计的四腔矩形波导滤波器通过使用CQ交叉耦合结构实现第1谐振腔与第4谐振腔之间的能量交换,其交叉耦合模型如图2所示。
谐振腔可以等效电容或电感用来存储电场或磁场能量。电容的阻抗计算公式为:

式中,C为电容,当其两端加载电压U时,电流为:
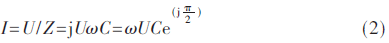
此时,电容的电流相位超前电压相位90°。
电感的阻抗计算公式为:

式中,L为电感,当其两端加载电压U时,电流为:

此时,电感的电流相位滞后电压相位90°。
故电耦合是阻抗为负纯虚数的耦合,具有+90°相位差;磁耦合为阻抗为正纯虚数的耦合,具有-90°相位差。滤波器可以等效为电容电感的串联,其阻抗为:

易知,ω=ω0时,Z=0;ω<ω0时,Z为正纯虚数;ω>ω0时,Z为负纯虚数。因此,当谐振腔处于高频端时,其阻抗为正,相位差为-90°,相当于电感;当谐振腔处于低频端时,其阻抗为负,相位差为+90°,相当于电容。
结合图2对本文设计的滤波器模型进行分析。若主耦合为容性耦合(电耦合),交叉耦合为感性耦合(磁耦合),通带低端的主耦合相位差为+90°-90°+90°-90°+90°-90°+90°=+90°,通带低端的交叉耦合相位差为+90°+90°+90°=-90°+360°,通带高端的主耦合相位差为-90°-90°-90°-90°-90°-90°-90°=+90°-360°-360°,通带高端的交叉耦合相位差为-90°+90°-90°=-90°,因此若信号幅度相等,相互抵消,会在通带低端和通带高端各产生一个传输零点。同理,若主耦合为磁耦合,交叉耦合为电耦合,通带低端的主耦合相位差为+90°+90°+90°+90°+90°+90°+90°=-90°+360°+360°,通带低端的交叉耦合相位差为+90°-90°+90°=+90°,通带高端的主耦合相位差为-90°+90°-90°+90°-90°+90°-90°=-90°,通带高端的交叉耦合相位差为-90°-90°-90°=+90°,因此若信号幅度相等,互相抵消,会在通带低端和通带高端各产生一个传输零点。但是当主耦合和交叉耦合都为电耦合或都为磁耦合时,主耦合和交叉耦合相位差相同,无法抵消,不会在通带两侧产生传输零点。
1.3 有无交叉耦合结构仿真对比
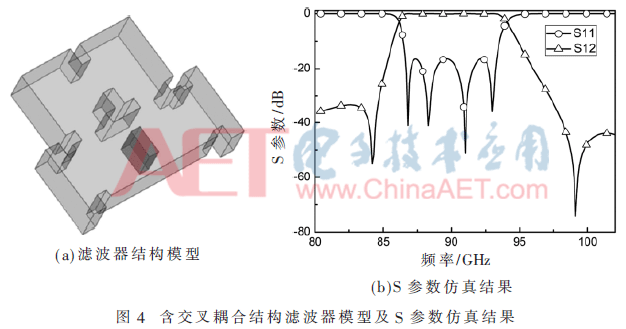
使用HFSS仿真软件对无交叉耦合结构的滤波器模型和有交叉耦合结构的模型分别进行了仿真和优化。无交叉耦合结构的滤波器模型和其S参数最终仿真结果如图3所示,含交叉耦合结构的滤波器模型及其S参数最终仿真优化结果如图4所示。通过对比图3(b)和图4(b)可以发现,加载交叉耦合结构后在通带两侧分别产生了一个传输零点。不含交叉耦合结构模型的30 dB带宽(18.2 GHz)与3 dB带宽(8.7 GHz)之比为2.09,而加载交叉耦合结构模型之后,其30 dB带宽(12.5 GHz)与3 dB带宽(8.0 GHz)之比为1.56。矩形系数(30 dB带宽与3 dB带宽之比)下降了25.7%,带外抑制明显得到了增强。

2 比例效应
矩形谐振腔的谐振频率与其各边长之间的关系如式(6)[6]所示。式(6)中,fmnl为矩形谐振腔模式频率,a、b、l分别为矩形谐振腔的长、宽、高。分别对80 GHz、90 GHz、100 GHz 3个中心频率的滤波器模型进行了仿真优化,优化后的参数尺寸如表1所示。表1中a、b分别为波导口长和高,t为膜片厚度,A1、A2分别为谐振腔1和4的长、谐振腔2和3的长,L为谐振腔宽,WS1、W12、W23、W34、W4L分别为谐振腔间膜片间距,WP为交叉耦合膜片宽度。

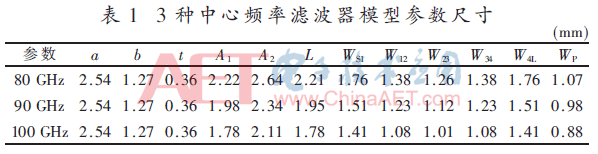
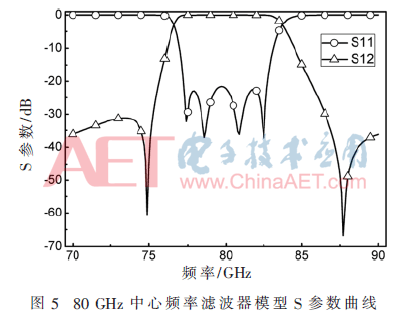
90 GHz中心频率滤波器模型的全波仿真S参数曲线如图4(b)所示,80 GHz和100 GHz中心频率滤波器模型的全波仿真S参数曲线如图5和图6所示。当滤波器的中心频率从80 GHz增加到90 GHz时,中心频率增加了11.1%,同时,腔体参数A1、A2、L分别减小10.8%、11.4%、11.8%,耦合结构参数WS1、W12、W23、W34、W4L、WP分别减小10.8%、10.9%、11.1%、10.9%、10.8%、8.4%。当滤波器的中心频率从90 GHz增加到100 GHz时,中心频率增加了10%,同时腔体参数A1、A2、L分别减小10.1%、9.8%、10.3%,耦合结构参数WS1、W12、W23、W34、W4L、WP分别减小10.2%、12.2%、9.8%、12.2%、10.2%、10.2%。通过上述对中心频率和其各个结构参数之间的分析,可以发现滤波器的中心频率与其整体结构参数之间存在着一定的相同的比例关系,为矩形波导滤波器不同中心频率模型的设计提供了实际依据。

3 参数扫描分析
为了研究矩形波导滤波器的各个性能指标(中心频率、带宽、插入损耗、回波损耗等)与其相关结构参数尺寸之间的内在关系,本文以90 GHz中心频率滤波器模型为例进行了具体的研究。
3.1 中心频率
谐振腔尺寸参数L的S参数扫描曲线如图7所示。从图中可以看到,参数L从1.92 mm增加到2.04 mm,滤波器的中心频率从90.8 GHz减小到88.3 GHz。参数L每增加0.03 mm,中心频率减小0.5 GHz,进一步证明了谐振腔参数与其中心频率之间的比例关系。

3.2 插入损耗
以参数W23为例,分析了耦合结构参数与回波损耗之间的内在关系。耦合结构参数W23的S参数扫描曲线如图8所示。当参数W23从0.9 mm增加到1.14 mm,滤波器的回波损耗曲线明显变好。其他耦合结构参数WS1、W12、W34、W4L等都会对滤波器的回波损耗产生一定的影响。
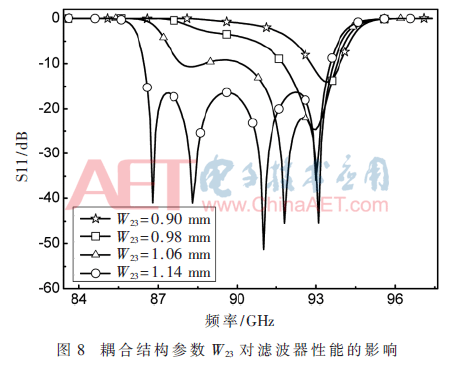
3.3 带宽
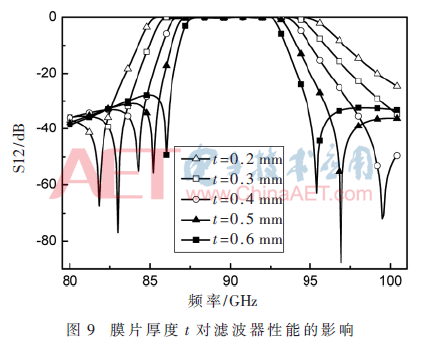
耦合膜片厚度t的S参数扫描曲线如图9所示。当膜片厚度t从0.2 mm增加到0.6 mm,带宽从11 GHz减小到5.4 GHz。但是,不管膜片厚度如何改变,矩形波导滤波器的中心频率没有发生改变。随着带宽的增加,滤波器的带外抑制相应下降,因此需要综合考虑带宽指标与带外抑制指标,设计出符合需求的滤波器。
4 加工与测试
基于SU-8厚光刻胶工艺对90 GHz中心频率矩形波导滤波器模型进行了加工,并对其电磁性能参数进行了测试。滤波器分为盖子和主体两部分进行加工,然后用银导电胶将两部分拼接在一起完成滤波器的加工。滤波器的趋肤深度为0.22 mm,滤波器表面溅射铜层厚度为0.7 mm,大于3倍的趋肤深度。溅射后的滤波器模型如图10所示。加工后的滤波器模型使用R&S ZV40网络分析仪进行了测试,测试结果与仿真结果的对比如图11所示。测试结果与仿真结果基本吻合,但损耗偏大,原因有很多,最有可能的原因是封装不严密。


RF MEMS器件封装方法分为多个层面,每个层面也有很多种不同的封装方法,如何选择取决于其本身的结构以及其对性能的要求。针对本文设计和加工的矩形波导滤波器而言,首先要优先考虑的是滤波器结构的优化,以降低封装带来的额外的损耗,其次需要考虑到器件对尺寸的要求,最后还要考虑到工艺的难度。本文设计的滤波器选择在结构设计过程中揉合对封装结构的设计,一共选择了卡槽式和盖板式两种拼接方法。卡槽式是在主体结构四周设计相应的卡槽,在对应的盖板上设计相应的卡板,最后用导电银胶粘合完成两部分之间的拼接。盖板式是直接在盖板边沿设计一圈包裹壁,将主体结构完全包住。
卡槽式封装可以明显降低辐射损耗,降低测试难度,但是其卡槽的深宽比较高,卡槽内的光刻胶不易清理,会给加工带来不小的难度。盖板式封装虽然容易加工,但是其损耗偏大,且不易测试。本文选择卡槽式最终来实现滤波器的封装,至于卡槽内的光刻胶显影问题,采用超声和注射器结合的方法解决。
5 结论
基于对矩形波导滤波器的研究与分析,本文设计了一款含交叉耦合结构的W波段矩形波导滤波器。滤波器的矩形系数因交叉耦合结构的加载而减小了25.7%,带外抑制明显增强。通过对滤波器各个结构参数的分析,研究了其与滤波器性能指标之间的内在关系,对矩形波导滤波器的设计有一定的参考意义。
参考文献
[1] DUAN J,ZHANG B,ZHANG A,et al.Microfabrication of a dual~mode rectangular waveguide flter[J].Microsystem Technologies,2016,22(8):2011-2016.
[2] REESE R,JOST M,JAKOBY R.Evaluation of two W-band power dividers in a subwavelength dielectric fibre technology[J].Electronics Letters,2016,52(16):1391-1393.
[3] SAMMOURA F,FUH Y K,LIN L.Micromachined plastic W-band bandpass filters[J].Sensors & Actuators A Physical,2008,147(1):47-51.
[4] HASEKER J S,SCHNEIDER M.90 degree microstrip to rectangular dielectric waveguide transition in the W-band[J].IEEE Microwave & Wireless Components Letters,2016,26(6):416-418.
[5] LIAO X,WAN L,YIN Y,et al.W-band low-loss band-pass filter using rectangular resonant cavities[J].IET Microwaves Antennas & Propagation,2014,8(15):1440-1444.
[6] LIU S,HU J,ZHANG Y,et al.1 THz micromachined waveguide band-pass filter[J].Journal of Infrared,Millimeter,and Terahertz Waves,2016,37(5):435-447.

