0 引言

    电力电子设备作为电力系统的关键部件，通常表现为连续性和离散型相互作用的混杂特性，对电力系统的可靠性具有重要影响^[1]。电力电子装置结构日渐复杂，其故障类型也越来越多，为确保电力电子装置安全、可靠、高效地运行，对其进行故障诊断研究并提高故障诊断准确率至关重要。

    现阶段故障诊断方法主要分为基于数据驱动和基于模型的故障诊断方法，前者需要大量的历史数据作为先验知识，后者需要建立系统的准确物理模型^[2]。而在基于模型的故障诊断中，往往没有考虑系统的参数不确定性，容易造成误报警。为解决这一问题，Armengol J等运用区间算法研究故障检测与诊断^[3]。Henry和Zolghari提出线性分式变换不确定性模型的滤波器方法进行残差生成和估计^[4]。Ilyas Rahal M等人建立线性分式变换的混杂键合图模型进行鲁棒故障检测与隔离^[5]。

    本文针对混杂系统的参数不确定性，提出运用BG-LFT建立系统参数不确定性DHBG模型，通过DHBG产生鲁棒残差和自适应阈值，以减少故障诊断的误报率。通过仿真来验证所提出方法在逆变器鲁棒故障诊断中的有效性。

1 基于键合图的系统不确定性建模

1.1 线性分式变换形式

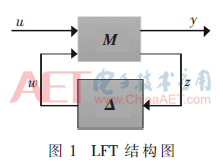
    线性分式变换(Linear Fractional Transformation，LFT)由Redheffer学者于1960年提出^[6]，在多变量不确定系统的鲁棒控制合成领域得到广泛应用。具有把系统解耦成确定部分和不确定部分的优点，是解决结构奇异值问题的有力工具^[7]，为构造系统的参数不确定模型提供了有效的途径。模型的LFT结构图如图1所示。确定部分用增广矩阵M表示，矩阵Δ表示所有的不确定性部分（结构的、非结构的参数或建模不确定、测量噪音等）。w和z分别表示系统的辅助输入和辅助输出；u和y分别表示系统的真实输入和真实输出。

1.2 参数不确定性的键合图建模

    运用键合图理论进行参数不确定性鲁棒故障诊断，通过建立系统的诊断键合图模型，可将解析冗余关系(Analytical Redundancy Relation，ARR)解耦为确定部分ARR_n=f(SSe，SSf，Se，Sf，MSe，MSf，u，θ_n)和不确定部分bn=f(SSe，SSF，δ_θθ_n)。其中，一个ARR表示为依赖系统参数(θ)的约束，SSe和SSf是检测器对偶化后的测量，(Se，Sf，MSe，MSf，u)分别表示已知输入，θ_n是标称参数，δ_θ是参数的不确定性。ARR的确定部分计算残差，不确定部分计算实时阈值。

    参数的不确定性δ_θ可表示为加性或乘性形式，如式(1)：

    其中Δ_θ和δ_θ=(Δ_θ)/θ_n分别表示为相对于参数θ_n标称值的绝对偏差和相对偏差。

    阻抗性R元件的乘性不确定性如图2。

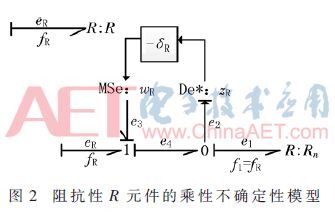
    阻抗型R元件的不确定性表示如下：

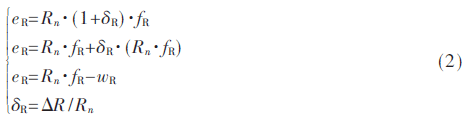
    其中R_n、δ_R、ΔR、e_R、f_R分别表示R元件的标称值、乘性不确定性、加性不确定性、势和流。w_R表示加入参数不确定性后势的虚拟输入。

    键合图模型中的“-”表示半定向箭头的源指向相应的结点。符号De^*和Df^*是虚拟传感器。其他元件的乘性不确定性参照阻抗性R元件。

2 鲁棒解析冗余关系和残差估计

    通过以下3个步骤得到系统的鲁棒ARR：

    (1)为避免模型的未知初始条件，键合图模型优先分配微分因果关系。

    (2)基于覆盖因果路径，0和1结点至少包含一个传感器。可推导ARR方程如下：

3 参数性故障诊断实例仿真

3.1 诊断键合图模型

    单相全桥逆变器共有2个桥臂，可以看成由两个半桥电路组合而成。把V1和V4作为一对，V2和V3作为一对，成对的两个IGBT同时导通，两对IGBT交替导通180°，结构如图3所示。

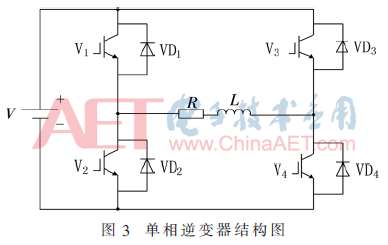
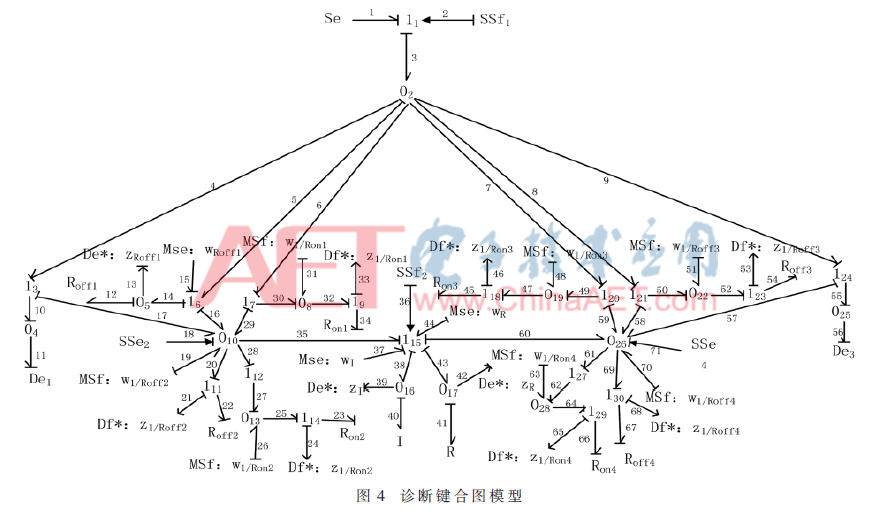
    对单相全桥逆变器进行故障诊断，需建立其对应的诊断键合图模型。因此，通过引入虚拟势（流）传感器将键合图模型中的电压（电流）作为输入，且在诊断模型中需尽可能地将传感器进行对偶化处理^[9]。而有些传感器不能产生解析冗余关系，不需要将其对偶化^[10]。根据上述分析，为系统重新分配因果关系，建立单相全桥逆变器的故障诊断键合图模型，如图4所示。

3.2 鲁棒解析冗余关系

    根据图4所示的诊断键合图模型，从而可得到鲁棒ARR分别的两个分离部分：

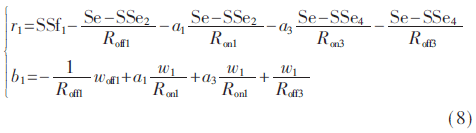
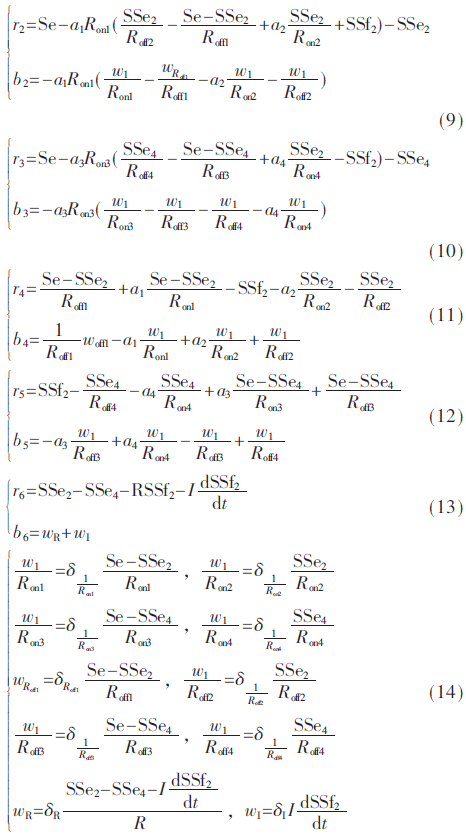
    其中，Se是已知输入，SSe_i和SSf_i是检测器对偶化后的测量，w_1/Roni、w_1/Roffi和w_Roffi是各元件参数所对应的虚拟输入，δ_Roffi、δ_1/Roffi和δ_1/Roni是各元件参数的乘性不确定性。

3.3 仿真结果

    当系统无故障时，残差的值近似等于零或者处于小幅度的波动状态但不超过阈值的上下界限。若系统中对故障敏感的残差明显偏离零值甚至超过阈值的范围，则认为系统中有故障发生并给以报告。如果残差在(-δ_θ，δ_θ)范围内，由元器件参数不确定性对系统或者残差造成影响不应该造成报警，此时不认为系统或者元器件发生了故障。

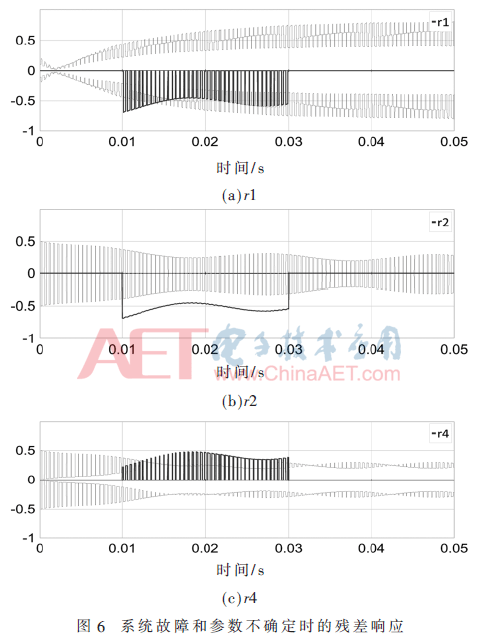
    在仿真中，参数的不确定性系数δ_θ为0.05。仿真结果如图5和图6所示。图5表示在系统无故障和所有参数不确定时，残差全为0。如果残差超过阈值，则系统故障。引入元件R_on1参数性故障，分析解析冗余关系可知残差r₁、r₂和r₄对此故障敏感，从图6可看出，残差r₁、r₂和r₄明显超过自适应阈值范围，触发故障警报，R_on1故障被有效地检测出。

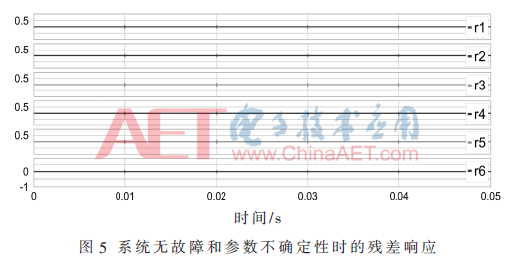
4 结论

    本文针对混杂系统中存在参数不确定性，传统的故障诊断方法无法减少误报警的问题，提出运用BG-LFT建立系统参数不确定DHBG模型，结合自适应阈值评价残差，对系统进行鲁棒故障诊断，能准确检测出系统故障，有效降低误报率，并在单相全桥逆变器中得到了验证，实验结果表明该方法是有效的。

参考文献

[1] 王文辉，刘帅，周东华.混杂系统故障诊断方法综述[J].系统工程与电子技术，2006，28(12)：1853-1857.

[2] 赵文浩，阎威武.基于数据驱动的故障诊断研究[J].微计算机信息，2010(28)：104-106.

[3] ARMENGOL J，TRAVE-MASSUYES L，VEHI J，et al.A survey on interval model simulators and their properties related to fault detection[J].Annual reviews in control，2000，24:：31-39.

[4] HENRY D，ZOLGHADRI A.Norm-based design of robust FDI schemes for uncertain systems under feedback control: Comparison of two approaches[J].Control engineering practice，2006，14(9)：1081-1097.

[5] RAHAL M I，OULD B B，MEGHEBBAR A.Hybrid bond graph model based for robust fault detection and isolation[J].Proceedings of the Institution of Mechanical Engineers，Part I：Journal of Systems and Control Engineering，2016，230(2)：145-163.

[6] REDHEFFER R M.On a certain linear fractional transformation[J].Studies in Applied Mathematics，1960，39(1-4)：269-286.

[7] KAM C S，Dauphin-Tanguy G.Bond graph models of structured parameter uncertainties[J].Journal of the Franklin Institute，2005，342(4)：379-399.

[8] ROTSHTEIN A P，POSNER M，RAKYTYANSKA H B.Cause and effect analysis by fuzzy relational equations and a genetic algorithm[J].Reliability Engineering & System Safety，2006，91(9)：1095-1101.

[9] TOUATI Y，MERZOUKI R，BOUAMAMA B O.Robust diagnosis to measurement ucertainties using bond graph approach：application to intelligent autonomous vehicle[J].Mechatronics，2012，22(8)：1148-1160.

[10] BORUTZKY W.Bond graphs for modelling, control and fault diagnosis of engineering systems[M].Springer，2017.

作者信息:

彭冬梅，帕孜来·马合木提

(新疆大学 电气工程学院，新疆 乌鲁木齐830047)