0 引言

    目前，随着我国航空航天科学技术的发展，尤其是空间推进技术的大力发展，航天器空间模拟实验对实验设备的要求正在逐步提高。而超低温和高真空是模拟实验所重点要求的重要的测试环境。其中，真空泵是空间模拟器的核心设备之一，真空泵能否正常工作，将决定空间环境模拟器能否正常有效地完成航天器的真空热环境实验。其次，中国拥有大量的航空航天基地，还有冶金行业等，真空泵的持有数量巨大。因而，无论是从设备安全角度还是从社会经济利益出发，对真空泵运行故障进行检测都具有重要的意义。

    在传统的机械故障诊断技术中，傅里叶变换是最常用的频域信号处理方法，但是由于其自身的局限性，在面对非线性以及时频变化规律时稍显无力。而小波变换的取样步长随着频率的变化而变化，与实际生活中高频信号对时间分辨率要求高而低频信号对频率分辨率要求较高的特点相符合^[1]，因而更能满足在处理信号时对时域和频域的要求。

    奇异值分解(Singular Value Decomposition，SVD)是一种能够有效提取信号特征的方法，通过SVD得到的奇异值表征着数据的固有性质，其稳定性和不变性较好^[2-3]。研究表明，通过对信号进行SVD后再进行信号重构，能够有效去除信号中的噪声，留下有用的信息^[4-5]。通过构造信号的吸引子轨迹矩阵，并对之进行SVD，通过计算选择适当的奇异值来进行信号重构，就能剔除掉信号中的随机部分，最大程度保留信号的有用部分，达到信号去噪。

    支持向量机(Support Vector Machine，SVM)是一种被广泛应用于模式识别的机器学习方法，其基本的理论原理是统计学理论。在处理高维数、非线性、小样本的问题中，SVM具有较强的优势，因而本文选取SVM进行故障模式的识别^[6]。

    本文结合SVD和小波包变换，实现真空泵的故障特征提取，再将提取的特征向量输入到SVM中，从而实现真空泵的故障识别。

1 奇异值分解（SVD）

1.1 SVD原理

    对于采集到的时间信号x(n)，其长度为N，n=1，2，3，4，…，N，对其进行相空间重构，其采样间隔为τ，则重构的吸引子轨迹矩阵A为^[7]：

1.2 基于SVD的信号去噪方法研究

    对于采集的时间序列x(n)，有用信号和噪声混杂其中。根据研究，若信号为光滑信号，那么其吸引子轨迹矩阵的秩r<min(L，M)；若信号含有一定的噪声，那么其吸引子轨迹矩阵的秩r=min(L，M)^[8]。在对SVD的研究中发现，相比光滑信号的奇异值主要分布在前k个上，噪声信号的奇异值对各维度的贡献基本相等。因而，对时间序列x(n)进行SVD，得到r个奇异值，按大小依次排列为α₁，α₂，…α_k，…，α_r，信号的有用信息主要集中在前k个奇异值上，后r-k个奇异值更多表征着噪声信息。为了去噪，可以去除后r-k个奇异值，将其设置为零，得到一个新的对角矩阵Λ′：

    关于分离阶数k的选取，为了尽可能保留有用信号，可以利用奇异值的贡献率来选择，贡献率ρ定义如下：

    一般认为贡献率大于等于0.9时可以基本保留原信号的有用信息。

2 小波包分解(WPD)

    相较于小波分解，小波包能够对上一层分解得到的高频频段进行进一步分解，从而能够提高信号的时-频分辨率，具有更高的应用价值^[10]。

    WPD算法为：

    由Parseval公式，x(n)的小波包系数C_j，k的平方具有能量量纲，所以选用WPD得到的能量谱来表征信号的能量分布是可行的。

3 实验系统与故障特征提取

3.1 实验数据的采集

    整个采集平台由一个上位机、NI公司的采集卡6366、前置放大器和一个传感器构成。采集卡的采样率最高可达2 MS/s，并且支持8通道同步进行采集。传感器采用的PAC公司的R3α，其中心频率为29 kHz。

    实验采集真空泵在正常运转与过载情况下的振动信号，采样率是100 kHz，每组采集5 000个点。采集130组数据，前60组作为SVM的训练样本，后70组数据作为SVM模型的校验样本。采用中科科仪公司生产的110分子泵机组进行实验，使用PAC公司的R3α进行采集，最后选择合适的实验样本进行分析。

3.2 信号的特征提取

    经过采集系统，得到真空泵的振动信号x(n)，图1即为采集到的过载信号原始图。

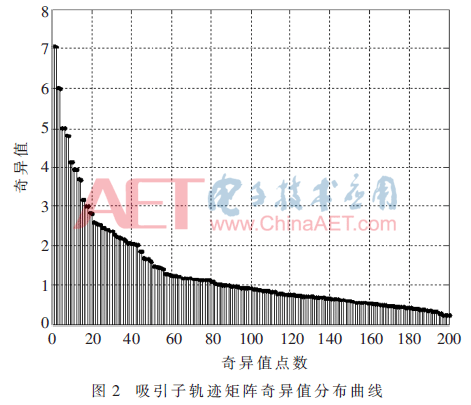
    根据前面提到的，对原始过载信号x(n)进行奇异值分解去噪。首先计算x(n)的自相关函数，从而得到吸引子轨迹的延迟步长τ。经计算，τ为6。根据已经确定的延迟步长，对信号进行奇异值分解，奇异值分解如图2所示。选取嵌入维度为200，x(n)长度为5 000。选择根据贡献率来选定奇异值，本文保留90%的奇异值，经计算，对于测试信号，保留前142个，对后58个置零并进行信号重构，这样就得到了去噪后的测试信号。对去噪后的真空泵的正常和过载信号用db11小波进行7层WPD，通过小波包的分解与重构，选取能量集中的前8个频段，如图3～图6所示。其中，纵坐标表示幅值，s70、s71…s77分别表示第7层的第1、2…8个频段。

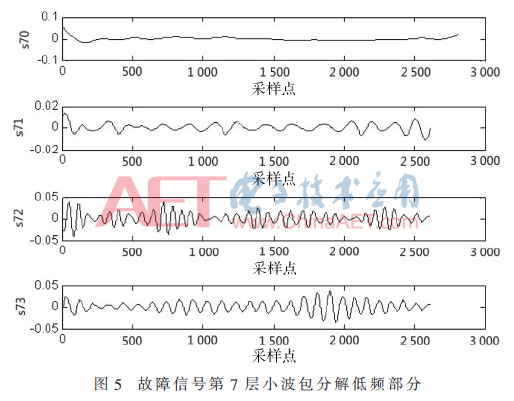
    对于得到的8个有效频段，分别求其能量：

    这样，可以得到一个由频段能量组成的8维向量[E₀，E₁，E₂，E₃，E₄，E₅，E₆，E₇]，得到的小波包能量谱如图7所示。

4 模式识别

    支持向量机(SVM)是由Vapnik首先提出的，现在学者们常常将之用来解决线性回归以及模式识别的问题。SVM的解决问题思路是寻找一个适当的超平面来作为分类曲面，使得想要区分的样本之间的隔离边缘达到最大^[12]。

    测试信号首先进行SVD去噪，再经过7层WPD，得到第7层的8个频段的能量组成的8维向量作为SVM的输入。正常工作下的信号输出为1，故障情况下的输出为-1。 测试结果如图8所示。   

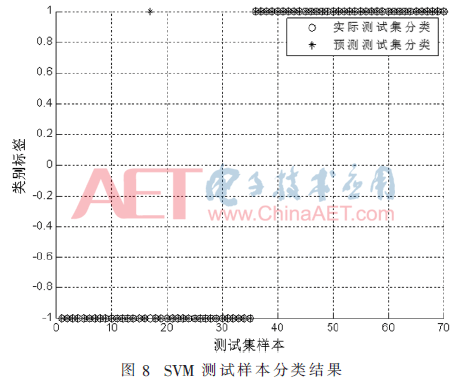
    可以看到，SVM对故障和正常信号的判别正确率达到98.57%。这说明通过奇异值去噪和WPD提取的能量向量作为故障的特征信息是可行的。用训练样本对SVM进行训练，再对其用测试样本进行检验，得到的结果与实际符合，因而用SVM进行故障识别具有很强的可靠性。

5 结论

    本文结合SVD、WPD以及SVM进行真空泵的故障识别。SVD能较好地去除信号中的无用噪声，再通过小波包的分解与重构来进行特征提取作为SVM的输入向量，具有非常高的准确率，能够准确高效地识别出真空泵的故障。因而，基于SVD、WPD以及SVM的真空泵故障诊断方法是有效可行的。

参考文献

[1] 葛哲学，沙威.小波分析理论与MATLAB R2007实现[M].北京：电子工业出版社，2007.

[2] 温广瑞，张西宁，屈梁生.奇异值分解技术在声音信息分离中的应用[J].西安交通大学学报，2003，37(1)：37-40.

[3] 李亚安，王洪超，陈静.基于奇异谱分解的水声信号降噪方法研究[J].系统工程与电子技术，2007，29(4)：524-527.

[4] 吕志民，张武军，徐金梧，等.基于奇异谱的降噪方法及其在故障诊断技术中的应用[J].机械工程学报，1999，35(3)：85-88.

[5] 刘献栋，杨绍普，申永军，等.基于奇异值分解的突变信息检测新方法及其应用[J].机械工程学报，2002，38(6)：102-105.

[6] 张超，陈建军，郭迅.基于EMD能量熵和支持向量机的齿轮故障诊断方法[J].振动与冲击，2010，29(10)：216-220.

[7] 段向阳，王永生，苏永生.基于奇异值分解的信号特征提取方法研究[J].振动与冲击，2009，28(11)：30-33.

[8] 赵艳菊.强噪声背景下机械设备微弱信号的提取与检测技术研究[D].天津：天津大学，2008.

[9] 陈恩利，张玺，申永军，等.基于SVD降噪和盲信号分离的滚动轴承故障诊断[J].振动与冲击，2012，31(23)：185-190.

[10] BOGGESS A，赵树森.小波与傅里叶分析基础[J].国外科技新书评介，2010(4)：2.

[11] 孙洁娣，靳世久.基于小波包能量及高阶谱的特征提取方法[J].天津大学学报(自然科学与工程技术版)，2010，43(6)：562-566.

[12] MATLAB中文论坛.MATLAB神经网络30个案例分析[M].北京：北京航空航天大学出版社，2010.

作者信息:

李一博，沈  慧，高  远

（天津大学 精密测试技术与仪器国家重点实验室，天津300072）