文献标识码: A
DOI:10.16157/j.issn.0258-7998.173901
中文引用格式: 高正中,郭娜,李煜. 重复控制自适应PI控制器在APF中的应用[J].电子技术应用,2018,44(3):60-63,71.
英文引用格式: Gao Zhengzhong,Guo Na,Li Yu. Application of repetitive control and adaptive PI controller in APF[J]. Application of Electronic Technique,2018,44(3):60-63,71.
0 引言
电网中谐波的大量存在对电力系统的正常运行提出了挑战。为了更好地进行谐波处理,有源电力滤波器(APF)的设计与应用成为一大热点。其设计的原理是通过采集系统中三相负载电流含量,计算其基波电流值,两者做差即为相应的谐波电流分量[1],然后将此反向分量送给三相电源,完成对电网中谐波的抑制。三相四线制系统中因为不平衡电流的存在,在处理谐波同时,也需要完成对中线电流的补偿。
1 系统模型
系统结构采用四桥臂模型,在电容分裂式模型基础上多一个桥臂,用此桥臂实现中线电流的补偿,四相桥臂分别对应特定相电流进行跟踪,发挥补偿作用。不同于三桥臂结构需要对直流侧电容进行平衡,缩小电容电压差,而且电路相对复杂,四桥臂结构可直接对中线电流进行补偿,电路相对简单。APF拓扑结构及工作示意图如图1所示。
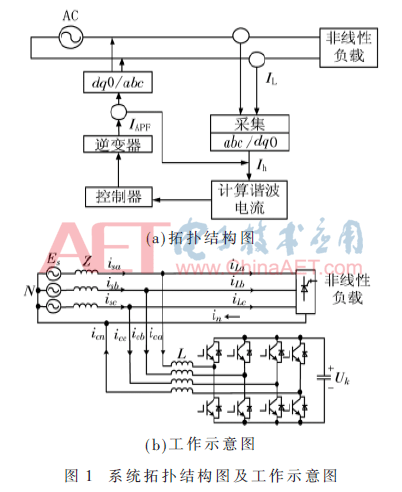
由图1所示,列基尔霍夫方程:

系统采集三相电流 ica、icb、icc和中线电流in,测得电流中所含有的谐波含量,实时传输到控制器对系统进行跟踪产生补偿电流量,输送到对应相进行补偿。
2 复合控制算法
系统通过ip-iq法得到补偿指令信号,指令信号传输到控制器,控制器需完成对谐波的抑制过程。
2.1 复合控制算法构成
PI控制算法简单[2-4],跟踪速度快,但是稳态性能差;重复控制稳态性能好,但是跟踪滞后一个周期[5],因此在对PI算法和重复算法进行研究的过程中,提出PI与重复控制并联的模型,其基本模型如图2所示。

2.1.1 PI控制器
由图2可知PI部分的闭环传函为:

2.1.2 重复控制器
重复控制算法的核心是内模原理,内模主要是指对外部信号的一种描述[6],包含指令信号和扰动信号两部分,使系统在跟踪指令信号的同时,消除外部扰动影响,这种动态反馈控制系统具有良好的稳态性能。离散模型如下:

其中,z-N是周期延迟环节。
由于系统基波信号是呈周期出现的,而且含有的谐波是基波周期的整数倍,因此认为外部信号是周期性变化的。z-N的作用是将此周期误差值经过延时作用于下周期的控制量。
另一重要组成部分是补偿器。补偿器根据所控对象P(z)的具体特性进行参数设置[7],根据上一周期已经采集到的数据与这周期内所测得的误差,对所控对象的相位和幅值进行补偿修正,每周期误差进行累加直到误差为零[8],不再存在修正参数时,会保持原值不变。其模型为:

2.2 自适应PI
当系统中负载发生变化时,上述并联控制器能够在一定时间内重新进行跟踪,但是效果不理想。针对PI算法的这一缺点,提出神经网络PI算法构成自适应PI控制器,迅速调节参数以保持整体状态,其基本结构如图3所示。
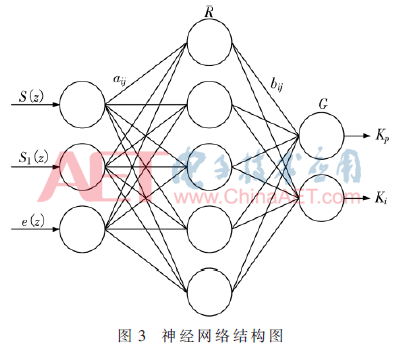
神经网络由3节点的输入层(输入量分别为指令量 S(z)、实际输出 S1(z)和误差 e(z))、2节点输出层(自适应PI参数Kp和Ki)和5节点隐藏层构成。
R函数为隐层输出函数,采用Sigmoid函数:

G为输出层函数,由于其输出值具有非负性,因此采用:

首先选定系统结构,确定每层权值的初始数,选择相应的学习速率及惯性系数;将输入值S和S1输入系统,即可得到Kp和Ki,系统通过权值的学习,调整各层加权参数,实现自适应PI参数的自动调节。
3 仿真及分析
根据系统拓扑结构及基本参数,建立Simulink模型[10]。负载由整流桥和三相串联RLC电路构成,为了试验效果,在A相接一个电感负载以产生中线电流。
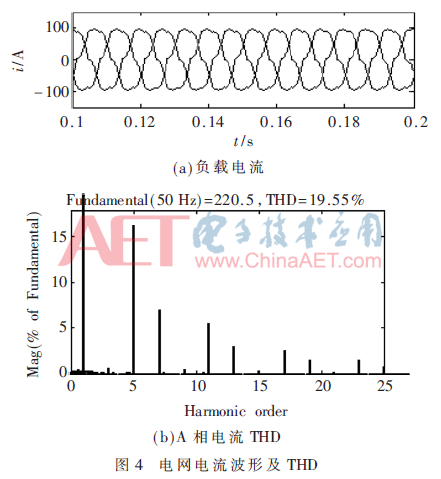
对系统中负载电流进行测量,其波形如图4(a)所示。由于谐波分量的存在,波形畸变严重,以A相为例,测得THD为19.55%,如图4(b)所示。
为了检验改进后的补偿效果,分别对3种算法进行Simulink仿真实验,设置补偿初始时间为0.1 s,图5为采用PI控制法、重复控制法及并联控制策略进行谐波补偿时系统测得的THD值,图6(a)为改进后的三相电流波形图,测得的A相THD值如图6(b)所示。
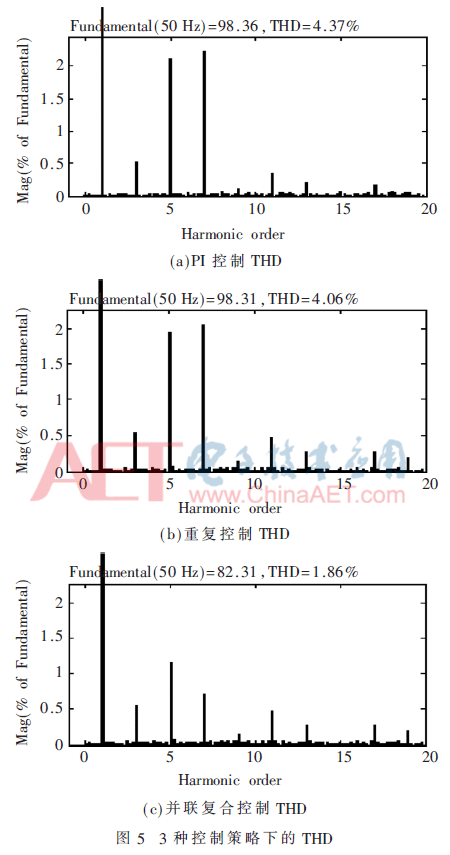
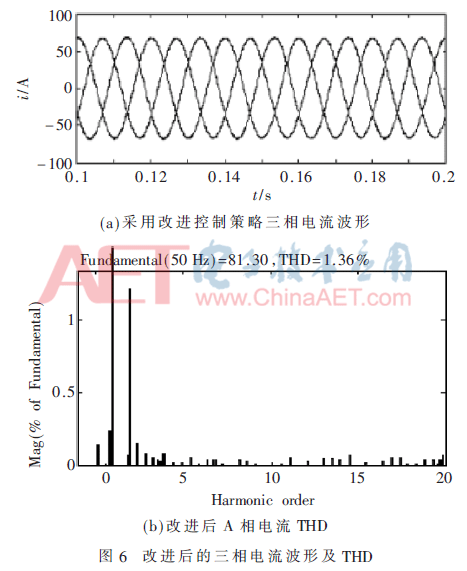
采用PI控制和重复控制对电网电流进行补偿时都使波形有趋于正弦波的趋势,但是不能达到很好的效果,补偿后电流波形不是平滑的正弦波。采用PI控制和重复控制时,其THD分别是4.37%和4.06%,采用重复控制虽然相比于PI控制畸变率降低,但效果并不明显,即两种控制的效果均不理想。将两种控制方法并联后,得到THD为1.86%,在此方法下谐波得到一定的控制。而采用改进的自适应结构后,电流波形基本接近基波波形,三相对称,其谐波含量降低为1.36%,比简单并联时又降低了30%,因此采用改进控制器抑制谐波具有显著效果。
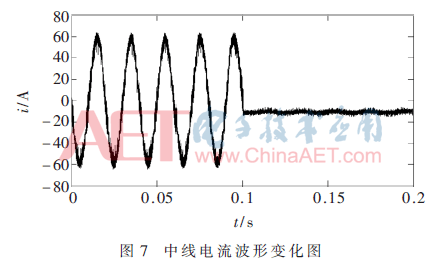
三相不平衡负载使系统出现中线电流,中线电流的存在会导致系统出现发热现象,严重时会烧坏电子器件,令APF无法正常使用。如图7所示,系统中线电流幅值达到60 A,设置APF在0.1 s进行补偿操作,补偿后的中线电流可以控制为在一定的范围内波动,比较平稳,控制效果较好。
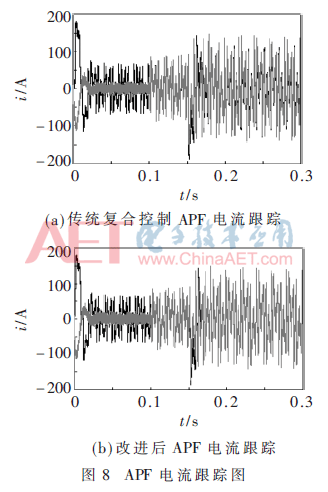
为研究APF在系统负载发生突变的情况下补偿效果,在0.15 s突加负载,系统迅速完成对各相电流的跟踪及补偿。控制器对指令电流进行跟踪,0.1 s以前APF输出电流为零,当APF开始工作以后,迅速跟踪指令电流,在0.15 s当负载发生突变时,指令电流变大,APF在极短时间内对新的指令电流进行跟踪,输出补偿电流。图8为APF电流跟踪情况,可以发现采用简单并联模型对中线电流进行追踪,其效果不如改进后效果理想。
仿真结果表明,采用复合控制对三相四线制电路进行谐波补偿时,其抑制效果明显,电网电流中谐波含量显著下降,波形近似正弦波。当系统发生负载突变时,APF在一个周期内迅速跟踪变化的指令电流,调整输出补偿电流,使电网电流重新达到三相平衡。
4 结论
在低压配电网中,系统中含有大量谐波成分,阻碍系统的运转和发展,当负载出现不均衡时,就会出现中线电流,它的存在也会对电网产生影响。本文通过对比传统PI、重复控制器、简单并联控制器和自适应复合控制器的谐波控制效果,发现改进控制器对系统谐波具有更好的控制作用,提高了供电质量,基于复合控制的APF具有较高的应用价值。
参考文献
[1] 王兆安.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2016.
[2] 吴敏,兰永红,佘锦华,等.线性不确定系统的H∞状态反馈鲁棒重复控制[J].控制理论与应用,2008,25(3):427-433.
[3] ABU-RUB H,GUZINSKI J,KRZEMINSKI Z,et al.Predictive current control of voltage source inverters[C].Industrial Electronics Society,2001.IECON′01,the 27th Annual Conference of the IEEE,2001,2:1195-1200.
[4] 孙鸣,庞辉,丁明.基于PWM控制的无功补偿装置的原理与仿真研究[J].煤炭学报,2004,29(6):744-747.
[5] 陈国柱,吕征宇,钱照明.有源电力滤波器的一般原理及应用[J].中国电机工程学报,2000,20(9):17-21.
[6] COSTA-CASTELL,GRINO R,FOSSAS E.Odd-har-monic digital repetitive control of a single-phase current active filter[J].IEEE Transactions on Power Electronics,2004,19(4):1060-1068.
[7] Zhou Keliang,LOW K S,WANG D,et al.Zero-phase odd-harmonic repetitive controller for a single-phase PWM inverter[J].IEEE Transactions on Power Electronics,2006,21(1):193-201.
[8] 马迎召.基于改进重复控制的有源电力滤波器研究[D].长沙:长沙理工大学,2010.
[9] AKAGI H,NABAE A,ATOH S.Control strategy of active power filters using multiple voltage-source PWM converters[J].IEEE Transactions on Industry Applications,2008,IA-22(3):460-465.
[10] 梁营玉,刘建政,许杏桃,等.基于电源电流和负载电流检测的前馈加反馈的三相四线制APF控制策略[J].电力自动化设备,2015,35(1):94-100.
作者信息:
高正中,郭 娜,李 煜
(山东科技大学 电气与自动化工程学院,山东 青岛266000)

