0 引言

    人体在自发运动或者肌肉在受到外界刺激时产生的信息在检测电极处时间和空间的叠加构成了表面肌电信号^[1]。该信号作为仿生假肢的控制源信号已经成为人工智能领域的重要应用。手臂肌电信号的幅度在10 mV以内，其能量主要集中在20 Hz～500 Hz频段^[2]。由于各种环境因素的存在，使得肌电信号的获取经常受到干扰，其噪声来源主要有以下几种^[3-4]：(1)检测电路中大多电子元件本身工作存在噪声；(2)检测各种肌电信号时，电极跟皮肤接触产生的伪信号；(3)由其他电场辐射引起的电磁干扰等噪声。因此，如何提高手臂肌电信号识别的准确率，成为重要的研究领域。

    传统消除肌电信号干扰算法有很多，如卡尔曼滤波法、谱相减法等算法^[5]。这些传统处理方法对于去除含噪肌电信号是比较困难，去噪效果特别不明显。DONOHO D L等学者提出基于小波的阈值去燥理论^[6]，这种方法在微弱电信号处理、图像去噪处理等领域应用广泛。

    常用的基于阈值的小波去噪方法有软阈值和硬阈值选取法^[7-8]。本文研究了软、硬阈值存在不连续点和恒定偏差等缺点，引入非线性函数，并且利用控制系数，以此对小波阈值去噪算法进行改进。改进的小波阈值去噪方法可以有效提高肌肉电信号去噪效果，促进后期信号识别的准确性和可靠性。

1 小波变换理论分析

    常用的小波滤波方法包括贝叶斯法和非贝叶斯法[9]。非贝叶斯法又分为3种方法：(1)空域相关滤波算法；(2)模极大值重构滤波算法；(3)小波阈值滤波。通过分析比较3种滤波方法得出，小波阈值滤波算法具有实时操作简单、计算量小等特点，所以本文对小波阈值去燥方法展开研究。

    通过研究分析，由于经过小波变换后，C_j会产生很多的冗佘量，因此对含噪信号进行去噪和恢复处理可以利用这个冗余性。当满足一定条件时，f(t)能够构成平方可积函数的基函数，则可以用平方可积函数中的一组基线性表示。经过理论分析，该小波变换生成基的方式简单。

2 基于改进的阈值算法

2.1 基于阈值的小波去噪方法

    在去噪过程中，通过优化选择阈值来提高信号去噪的效果是本文主要研究内容。基于阈值的选取方法包括软阈值和硬阈值两种，介绍如下：

    (1)硬阈值函数分析

    硬阈值函数如式(5)所示^[11]：

其中，λ为设定的门限阈值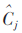，为阈值滤波后的小波系数。当小波系数C_j小于-λ或者大于λ时，这部分小波系数被认定为原始信号的小波系数；相反，小波系数为0。

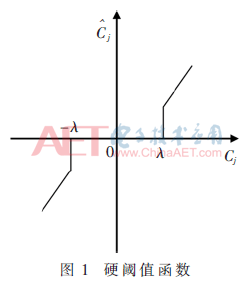
    基于硬阈值小波去噪方法可以获得具有相似性较强的重构信号。但是在该方法中信号边缘容易产生振荡阈值，形成突变信号。其函数曲线图如图1所示。

    （2)软阈值函数

    软阈值函数如(6)所示^[12]：

式中，当C_j大于λ时，小波系数减去λ；当C_j小于λ时，小波系数加上λ，这些可以作为重构对象；当C_j处于-λ和λ之间时，滤除掉这部分小波系数，处理后的小波系为0。

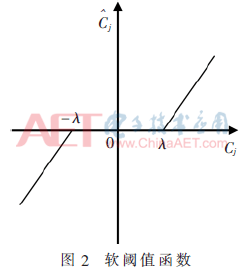
    通过基于小波软阈值去噪法可以获得具有较好光滑性的重构信号。但是该方法中设定的阈值是有偏差的，会导致滤波后的信号有时会过于平滑，从而导致误差较大。其函数曲线图如图2所示。

2.2 改进阈值去噪法的分析

    在肌电信号去噪的初始阶段，硬阈值算法虽然会获得相似性较强的重构信号，但由于其门限阈值函数是有跳变的，其在含有多重振荡信号中会产生许多突变噪声点，这时，滤波后的信号出现许多失真现象^[13]。对于软阈值算法函数来说，虽然它是一个连续函数，其在处理振荡信号的小波系数时，会显得较为平滑，很大程度上克服了硬阈值算法的缺点。同样该算法对绝对值大的小波系数有较大的影响，还会造成信号高频分量信息的损失，使处理后信号过于平滑，导致信号边缘模糊，也会在重构信号中增大误差。为此，在函数过渡阶段引入一个非线性函数与控制系数，就可以利用这样的阈值函数设定阈值参数。

    通过以上对软、硬阈值函数优缺点的分析，本文采用非线性函数进行过渡，同时引入控制系数，改进的阈值算法的表达式如式(7)所示。

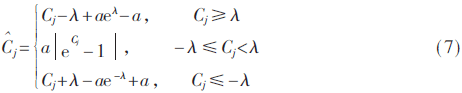
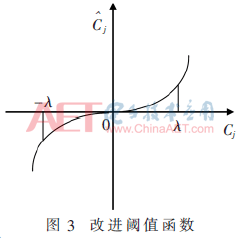
式中，a为引入的控制系数，在不同范围内，a都影响小波系数C_j在该区域内的变化程度。其函数曲线图如图3所示。

    小波软阈值方法计算出的估计值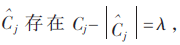为使重构后的信号无限接近原始信号，就要减小这个偏差。因此，本文提出的改进阈值法就是为了减小这个偏差，但从实际应用中分析，这个偏差不可能减小为零。因为如果把偏差λ减小成零，这就成为了小波硬阈值方法，这样达不到改进效果。如果让之间，这样得出小波系数估计值就更加近似于原始信号。

    因此，由式(7)可知，基于改进的阈值函数不仅具有软阈值的连续性，还具有偏差比软阈值小等特点。在式(7)中，当a=0时，该阈值函数与软阈值函数等效；当a→λ/(e^λ-1)时，随着原始小波系数C_j的增大，估计值更加接近C_j。因此，改进后的阈值函数偏差比软阈值函数偏差小。本文提出的改进阈值函数是在软阈值函数基础上引入控制系数，使得原始信号和噪声信号之间过度相对平滑，经过滤波处理后的信号更加接近原始信号。该方法思路简单，有利于提高去噪效果。

2.3 3种阈值小波去噪方法仿真结果分析

    本文采用控制系数a=0.3对手臂表面肌电信号进行去噪实验分析，对同一个含噪声信号，分别利用软阈值、硬阈值及改进阈值去噪法进行仿真分析。以仿真结果与信噪比作为其性能指标，信噪比越高，去噪效果越好，更加能恢复出原始信号，以此验证改进阈值去噪法的可靠性及有效性。仿真结果如图4所示。

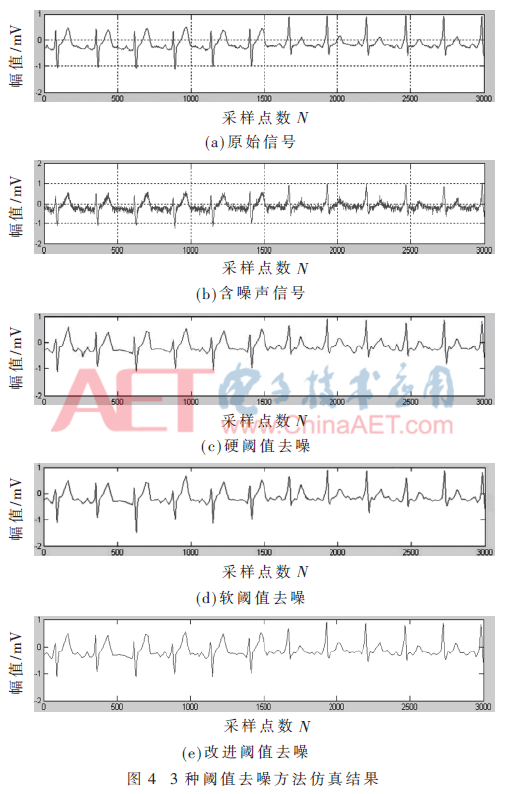
    由图4可知，硬阈值去噪算法产生了多余的突变噪声，软阈值去噪算法使得一部分频率点变得平滑，误差较大。改进阈值去噪法比软阈值去噪法减少了误差，比硬阈值去噪法更平滑，恢复出的信号更加近似于原始信号。为了克服软、硬阈值方法存在的缺点，利用改进阈值方法对表面肌电信号去噪的效果更好。对实验进行进一步的研究，将3种方法进行信噪比进行对比分析，其结果如表1所示。

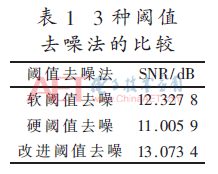
    由表1可以得出，在3种去噪结果中，硬阈值信噪比较低，改进阈值去噪法的信噪比最高。改进阈值去噪法保留了软阈值的连续性和平滑性，比软、硬阈值去噪法的去噪效果更好。因此，改进阈值去噪法可以应用在肌电信号去噪检测领域，而且有利于提高信号去噪的准确性。

3 基于改进阈值法处理含噪声信号

    在肌电信号中，需要考虑的噪声来源有：工频干扰、高频电磁场干扰、电极极化干扰、肌电干扰、测量仪器自身的干扰等。由于这些干扰信号的存在，使得在实际检测过程中采集到的肌电信号不够准确。将单通道获取到的肌电含噪声信号，利用小波变换处理后，得到一系列的小波系数。其中，有些小波系数包括原始信号的重要信息。原始信号对应的小波系数具有幅值较大、数量较少等特点。其他噪声对应的小波系数数量较多，但其幅值较小。因此，可以利用改进后的小波阈值去噪算法，将处理后的幅值较大的小波系数保留，将幅值较小的小波系数去掉。把滤波后剩余的小波系数进行构建函数，将恢复出原始信号与原始信号对比。本文利用改进后的阈值算法对含白噪声和工频干扰信号的肌电含噪声信号进行仿真分析，结果如图5、图6所示。

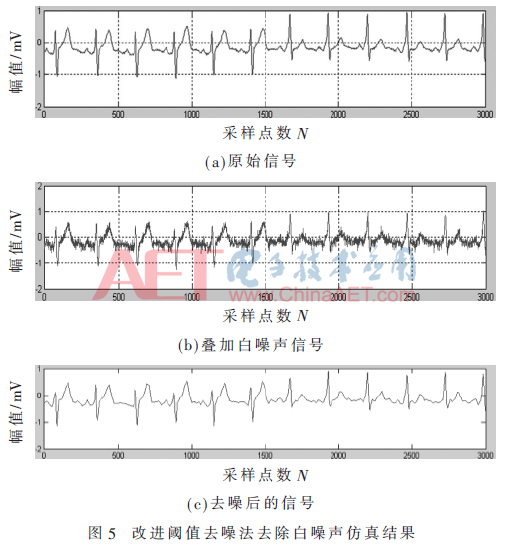
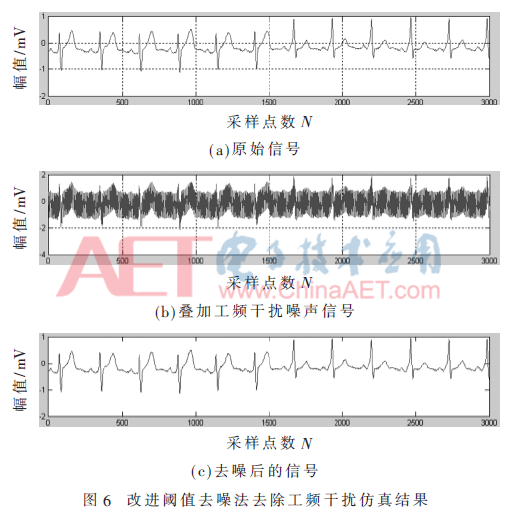
    对仿真结果进行对比分析可以得出，改进阈值算法在对叠加白噪声和工频干扰的混频信号处理时，减少了误差，处理效果更接近于原始信号。将处理后的肌电信号的信噪比进行对比分析，结果分析如表2所示。

    由表2可以得出，利用改进阈值小波去噪法处理含噪声信号具有较高的信噪比。

4 结论

    本文首先运用软、硬阈值去噪法及改进阈值去噪法对同一个含噪声信号进行分析处理，经过仿真分析得出改进阈值去噪法比软、硬阈值去噪法效果好，提高肌电信号的信噪比。其次，利用改进阈值去噪法对叠加白噪声与叠加工频干扰信号进行去噪处理，经仿真分析，该方法可以很好地抑制信号的零点漂移，能够准确地恢复出原始信号。

    本文在研究肌电信号去噪方法过程中，还有一些可以改进的地方。首先，本文是利用健康男性前臂肌肉电信号单通道的采集数据进行处理分析，选择控制系数a=0.3的情况下，对手臂表面肌电信号进行实验分析，在实际应用中，手臂运动涉及到多通道的肌肉信号检测；其次，对于残疾人的残肢，由于各种损伤等因素导致的意识减弱，不能简单地用单通道单个阈值作为判断方法。在今后研究设计中，应该根据个体情况，并利用多个通道的数据进行综合分析，优化算法，减少工作量，提高运算速度，才能确定个体的最佳特征参数和控制阈值。

参考文献

[1] GINI G，ARVETTI M，SOMLAI I，et al.Acquisition and analysis of EMG signals to recognize multiple hand movements for prosthetic applications[J].Appl Bion Biomechan，2012，9(2)：145-155.

[2] 曲峰.运动员表面肌电信号与分形[M].北京：北京体育大学出版社，2008.

[3] 赵章琰.表面肌电信号检测和处理中若干关键技术研究[D].合肥：中国科学技术大学，2010.

[4] 吴永亮，邱成，朱衡君.基于DAQ－2204的微弱信号数据采集与分析系统[J].测控技术，2011，30(3)：26-28.

[5] 孔玲军.Matlab小波分析超级学习手册[M].北京：人民邮电出版社，2014.

[6] DONOHO D L.De-noising by soft-thresholding[J].IEEE Trans.Inf.Theory，1995，41(3)：613-627.

[7] Li Guanlin，Li Yaonan，Yu Long，et al.Conditioning and sampling issues of EMG signals in motion recognition of multifunctional myoelectric prostheses[J].Ann Biomed Eng，2011，39(6)：1779-1787.

[8] SMITH L H，HARGROVE L J，LOCK B A，et al.Deter-mining the optimal window length for pattern recognition-based myoelectric control：Balancing the competing effects of classification error and controller delay[J].IEEE Trans.Neural.Syst.Rehabil.Eng.，2011，19(2)：186-192.

[9] 娄智，邓浩，陈香，等.基于自适应阈值处理的表面肌电信号小波去噪研究[J].生物医学工程学杂志，2014，31(4)：723-728.

[10] 王彦青，魏连鑫.一种改进的小波阈值去噪方法[J].上海理工大学学报，2011，33(4)：405-408.

[11] 叶裕雷，戴文战.一种基于新阈值函数的小波信号去噪[J].计算机应用，2006，26(7)：1617-1618.

[12] 段永刚，马立元，李永军，等.基于小波分析的改进软阈值去噪算法[J].科学技术与工程，2011，23(8)：5755-5758.

[13] 吴秀君.改进提升小波阈值算法在信号去噪中的应用[J].激光杂志，2014(8)：15-18.

作者信息:

刘明君1，董增寿2

（1.忻州师范学院 电子系，山西 忻州034000；2.太原科技大学 电子信息学院，山西 太原030024）