0 引言

    随着CMOS技术的不断发展，传统的MOSFET噪声模型已不再符合现代的要求。目前，对于MOSFET毫米波噪声的研究还仅限于器件的强反型区，而对器件弱反型区的研究少之又少。所以，如何建立一个完整统一的MOSFET毫米波噪声模型已然成为了国内外研究的热点和难点。传统的MOSFET高频噪声模型为^[1]：

    通过观察式(1)可以发现传统的MOSFET高频噪声模型存在以下几个缺点：漏极电流噪声模型只考虑了沟道热噪声而没有考虑散粒噪声；栅极感应电流噪声只考虑了栅极热电阻产生的热噪声，并没有考虑由沟道内的波动电势通过栅极电容的耦合效应引起的栅极极板的噪声电流；互相关噪声项并非不存在。

    本文针对以上传统模型存在的缺陷，基于40 nm MOSFET的器件物理结构并结合电荷守恒定律，依次提出了漏极电流噪声模型、栅极感应电流噪声模型以及互相关噪声模型。统一了模型在弱反型区到强反型区的表达式，引入有效栅极过载效应使得统一后的模型具有良好的平滑性、准确性和连续性。最终，通过将所建模型与传统的模型、实测的数据点进行对比，验证模型的有效性和准确性。

1 MOSFET的毫米波噪声建模

    图1为MOSFET小信号等效电路图。虚线框内为电路的本征部分，本征部分两端的噪声源分别为漏极电流噪声源S_id以及栅极感应电流噪声源S_ig，两者之间的相关性通过互相关噪声S_igid来表征。

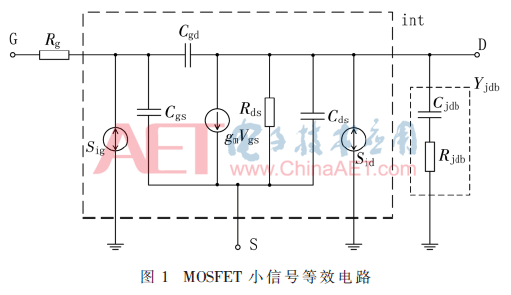
    下面就分别对漏极电流噪声S_id、感应栅极电流噪声S_ig以及两者之间的互相关噪声S_igid进行建模。

1.1 漏极电流噪声

    图2为NMOSFET的结构示意图，假设沟道源区与沟道界面为电势和坐标的零点，指定源极指向漏极为x坐标方向。设V₀(x)为沟道x处的电势，x附近单位沟道长度的电导为g(x)=g(V₀)，则源漏电流表达式为：

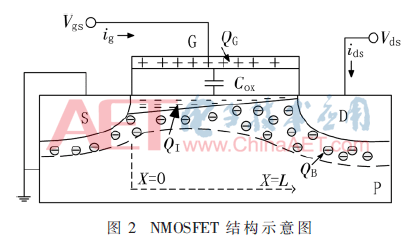
    短沟道MOSFET热噪声公式为：

其中V_ds为漏源电压，n为梯度因子，V_GT=V_GS-V_T为过驱动电压，μ_n为电子有效迁移率，L为有效沟道长度，W为沟道宽度，V_off为补偿电压，V_th=kT/q为热电压。

    当器件工作在毫米波段时，根据文献[2]的报导可知MOSFET的p-n结的散粒噪声为：

式中4kTg是附加噪声分量，g为增量电导。由式(8)可得MOSFET工作在毫米波段时的漏极电流噪声表达式：

式中δ为电荷系数。

    当器件工作在强反型区时，因不考虑衬底效应，V_GTeff可变为V_GT。等效电路模型下的栅极电阻也影响漏极电流噪声，所以强反型区下的漏极电流噪声可表示为：

1.2 感应栅极电流噪声

    感应栅极电流噪声包含栅极电阻产生的热噪声，以及由沟道内的波动电势通过栅极电容的耦合效应而引起的栅极极板的噪声电流^[4]。

    如图2所示，栅极感应噪声电流可表示为：

式中φ_S(x)为沿着沟道方向x处电势，ω为角频率。随着沟道长度的减小，沟道中漏源结的耗尽层占据比重加大，栅下硅表面形成的电荷量减少。当器件处于弱反型区时，沟道电流以扩散电流为主^[5]，所以弱反型区的漏极电流为：

    当器件工作在弱反型区时，反型层电荷浓度和耗尽层电荷浓度相比可以忽略不计，从源端到漏端的表面势可视为常数，通过求解泊松方程可得到沟道反型层电子密度为：

1.3 互相关噪声

    漏极电流噪声源和栅极感应噪声源都与偏置和载流子运动有关，由于栅-源电压的正电场吸引，使沟道中的载流子穿过多晶而到达栅极板间，所以电荷间的耦合作用促使了互相关噪声的形成。根据式(20)可以建立互相关噪声模型：

式中α为互相关噪声系数，这里同样为了模型能在弱反型区和强反型区都适用，引入有效栅极过载效应。式(27)可转化为：

2 结果与分析

    首先，利用MATLAB软件对本文提出的数学模型进行仿真，将仿真结果与传统模型仿真结果作比较，如图3所示。

    图3为所建模型以及传统模型的S_id、S_ig和S_igid*关于栅极过载电压的曲线图。图中实线代表着本文模型；虚线代表着传统模型。通过图3中的曲线对比可以观察出：图3(a)中的传统模型不适用于器件的弱反型区而本文模型可以，在强反型区本文的模型与传统模型的走势大体一致；图3(b)中两个模型的仿真结果有着一样的变化趋势；图3(c)中所建模型的仿真结果体现出了漏极电流噪声与栅极感应噪声之间的相关性，而传统模型则无法表征其相关性。由此可见本文所建的模型要优于传统模型。

    然后，本文基于HP8510网络分析仪和ATNnp5b微波噪声参数系统的实验平台，对栅指数N_f=10、栅宽W为2 μm、栅长L为45 nm、并联设备数M为6的MOSFET进行S参数的测量以及噪声系数F₅₀的测量。再分别提取出^[6]器件四噪声参数R_n、F_min、G_opt、B_opt的测量值。

    利用本文提出的S_id、S_ig以及S_igid*模型，根据式(30)～式(33)，可得四噪声参数的仿真计算结果^[4]。如图4所示，通过比较测量值与仿真结果的一致性，验证本文所建模型的有效性和精确性。

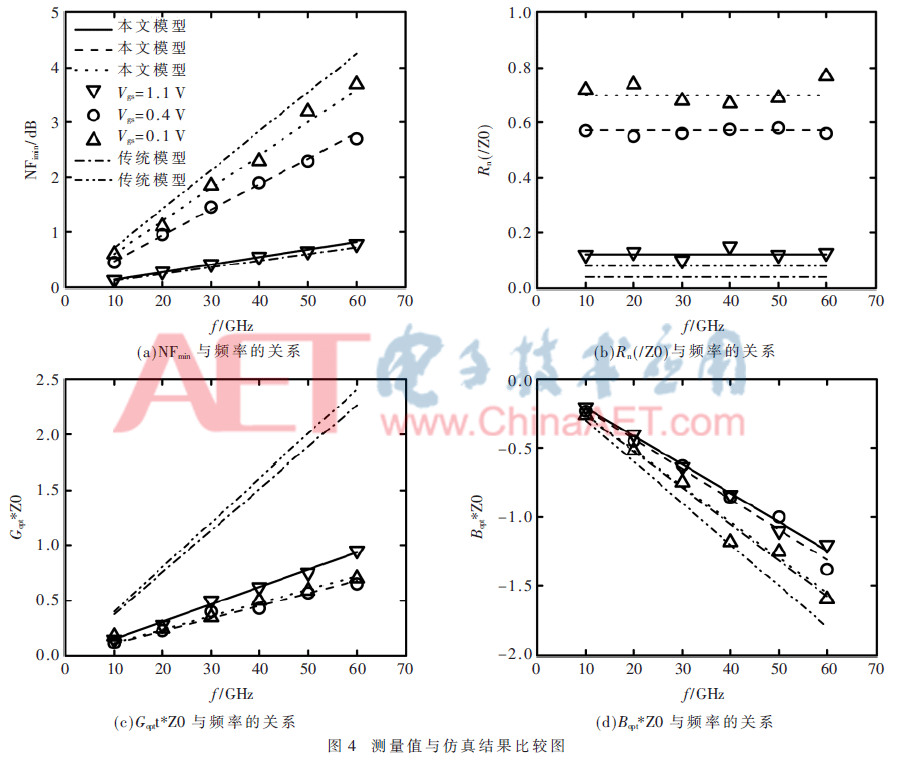
    图4为本文模型在不同反型区，不同频率点下与传统模型以及实测数据点的四噪声参数对比曲线图。实线、短线、点线分别代表所建模型在弱反型区、中反型区、强反型区的仿真结果；倒三角、圆圈、正三角分别代表着分布在弱反型区、中反型区、强反型区的实测数据点；线点线、线点点线分别代表传统模型在中反型区和强反型区的仿真结果。通过观察图4发现：本文所建模型的仿真结果在各个反型区都能与实测数据点相吻合，而传统模型不适用于弱反型区，并且在弱反型区和强反型区中它的变化趋势虽与实测数据相一致，但精度远不如本文所建模型。

3 结论

    本文通过对传统模型不足的分析，基于40 nm MOSFET的物理结构，重新建立了漏极电流噪声模型、栅极电流噪声模型以及两者的互相关模型。同时引入栅极过载效应,使得各模型的统一表达式在弱反型区到强反型区之间具有良好的平滑性。最后，通过对比不同反型区下的所建模型、传统模型以及实测点的四噪声参数，验证了本文模型的有效性和精准性。

参考文献

[1] NAVID R，JUNGEMANN C，LEE T H，et al.High frequency noise in nanoscale MOSFETs[J].J.Appl.Phys.2007，101：124501.

[2] ANTONOPOULOS A，BUCHER M，PAPATHANASIOU K，et al.CMOS small-signal and thermal noise modeling at high frequencies[J].IEEE Trans.Electron Devices，2013，60：3727-3733.

[3] CHAN L H K，YEO K S，CHEW K W J，et al.MOSFET drain current noise modeling with effective gate overdrive and junction noise[J].IEEE Electron Device Letters，2012，33(8)：1117-1119.

[4] CHAN L H K，YEO K S，CHEW K W J，et al.High-frequency noise modeling of MOSFETs for ultra low-voltage RF applications[J].IEEE Trans.Microw. Theory Techn.，2015，63：141-153.

[5] SPATHIS C，BIRBAS A，GEORGAKOPOULOU K.Semi-classical noise investigation for sub-40nm metal-oxide-semiconductor field effect[J].AIP Advances，2015，5：087114.

[6] LEE C I，LIN W C，LIN Y T.An improved cascade based noise de-embedding method for on-wafer noise parameter measurement[J].IEEE Trans.Electron Devices Lett.，2015，36：291-293.

作者信息:

彭小梅，赵爱峰，王  军

（西南科技大学 信息工程学院，四川 绵阳621010）