文献标识码:A
DOI: 10.19358/j.issn.2096-5133.2018.08.022
中文引用格式:喻永生,谢天异丹,刘畅,等.基于特征选择和HMM的股票价格行为研究[J].信息技术与网络安全,2018,37(8):96-100.
0 引言
股票市场已成为全球经济的一部分,如果能准确地预测股票市场的行为趋势,其高额的利益回报将具有巨大的吸引力。在早期的股票价格时间序列预测中,主要基于传统的统计学方法,如移动平均线(Moving Average,MA)[1]、自回归滑动平均模型[2]等。然而这类传统方法的性能受到了股票价格时间序列数据非线性性质的制约,其较强的非平稳性和潜在的周期性不能通过线性拟合得到充分体现。随着计算智能技术的发展,人工神经网络(Artificial Neural Network,ANN)[3]、支持向量机[4]和隐马尔可夫模型等技术也在股票价格时间序列预测领域开始得到尝试和应用。
隐马尔可夫模型(Hidden Markov Model, HMM)是分析和预测时间序列数据的常用工具。1994年,HMM模型首次被WEIGEND A S[5]应用在分析股票市场走势过程中。国内朱嘉瑜[6]基于ANN技术,结合粒子群优化算法和HMM,得到较传统模型效果更好的APHMM组合模型。HASSAN M R[7]利用航空公司股票数据训练HMM模型进行预测,模型达到近似ANN的效果,但没有解释模型隐状态含义。之后HASSAN M R 和NATH B[8]提出结合HMM、ANN和遗传算法的模型,预测效果接近自回归积分滑动平均模型,但仍存在直接指定隐状态数目的问题。LIEW C C和SIU T K[9]提出了将离散HMM模型转换为混合高斯模型,他们在解决期权定价问题时,将参数和状态运用HMM联系起来,同时也指出波动性和噪声干扰等不确定因素对其模型预测的影响。对于股票价格有效特征的识别,BARAK S[10]提出了基于滤波器和函数聚类方法的特征选择算法。段江娇[11]研究了HMM模型隐藏状态数量的选择问题,提出一种基于数据聚类来计算预测误差并自动调整HMM参数的算法,但算法的训练样本量在股价预测中难以达到。
HMM模型拥有坚实的数理基础,能够解释预测结果[7],有利改善预测性能。使用HMM对时间序列建模,其中最重要的问题是因子特征的选取和隐状态数目的确定。目前基于HMM的股票价格预测的研究中,隐状态的数目和输入特征因子往往是人为直接指定的,而这种指定方法没有明确解释,导致其模型的泛化能力和稳定性存在一定问题。为了使HMM预测模型有更好的性能,本文将着力于同时解决这两个问题。通过基于分类回归树的方法优化特征选取,运用贝叶斯信息准则(BIC)确定隐状态数目,旨在提出一个改进的HMM股价行为预测模型,以提高股票价格的预测精度,可用于股票市场的深入分析。
1 预测模型建立
1.1 隐马尔可夫模型
一个HMM分为两层,一层是隐藏的状态序列层,隐藏层是一个马尔可夫过程,也是有限状态机,其中每个状态之间有转换概率;一层是可见的观测层,是待识别的观测序列。在预测模型中,股票因子特征向量作为观测序列的值,通过识别状态序列的值来表示次日股价行为变化。
隐马尔可夫模型由状态转移概率矩阵A、生成概率矩阵B和初始概率分布Π确定,故HMM可描述为一个三元组,即λ=(A,B,Π)。
此外为了解决连续性观测序列值的影响,需要结合高斯混合模型(GMM)作为观测序列的概率密度函数,用于估计模型的生成概率。在模型参数训练上使用Baum-Welch算法,即输入观测序列数据集,估计HMM模型参数使得P(O|λ)最大。文献[12]对此算法进行了详细描述。
1.2 模型隐状态数目确定
BIC(Bayesian Information Criterion)方法可用于选择HMM模型隐状态数目。取预测指标F值(F-measure)作为模型对股价趋势预测的目标函数,用θ表示隐状态数目,Ck表示候选模型参数集中的第k项。基于BIC准则,最佳隐状态数目即BIC(Ck)取最大值时的参数。

其中n表示观测序列O的长度,k表示模型自由参数的总个数。
为了统计F值,要和样本真实值进行比较。根据在验证集中相应模型对每日股价涨或跌的预测结果统计TP、FP、FN值,从而计算F值来进行参数选择。
2 特征选择
在BARAK S的研究[10]中,他们分析公司财务指标和盈亏报表,并收集和预测股票收益和风险相关的特征,本文选取其中的部分与常见股票分析指标作为候选特征:ROA、ROE、销售净利润率、经营活动净收益、SMA、WMA、MOM、OBV、EMA。首先针对这些候选特征数据进行预处理。
2.1 候选特征数据预处理
(1)相关特征过滤
在候选特征之间,存在冗余的可替代特征。计算Pearson相关系数对互相关联性较高的特征进行过滤处理,可以为之后的工作缩减计算量。
Pearson相关系数公式如下:

其中,cov(X,Y)为特征X和特征Y的协方差值,σX为特征X的标准差,σY为特征Y的标准差。
在Pearson检验中相关系数rt达到重复阈值即rt≥rtmax的相关特征可进行去重。
(2)离群数据处理
采用基于密度最大值聚类算法识别股票特征的离群数据作为噪声处理。离群数据识别针对每一个股票特征进行单独聚类,一个特征数据对应一个聚类结果。要识别离群数据需要得到局部密度ρ和高局部密度点最小距离δ的值:
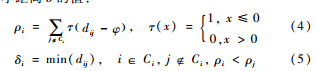
其中, C表示聚类过程中的划分簇,Ci表示包含数据项i的聚类簇,dij表示数据点i和j之间差值的绝对值,φ为距离阈值。
每个特征的所有数据项具有局部密度ρ和高局部密度点最小距离δ。在某个特征中选择局部密度低且高局部密度点最小距离最高的数据项作为离群数据,和其他对应时间戳特征的数据项一并进行剔除处理。
(3)缺失数据处理
综合数据量和股票性质,对于缺失数据进行均值插补法处理。
2.2 基于最小基尼指数的特征选取
特征选取基于CART(Classification and Regression Tree)方法,CART的核心是使用基尼指数划分特征。本文将特征的基尼指数作为特征选取的标准,使得划分后基尼指数越小的特征,最终将被选取的优先级越高。
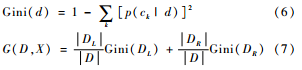
式(6)中,d表示CART树节点分裂后的左节点或右节点;ck表示类别集合中的第k个类。式(7)中,D表示数据集;X表示分裂阈值;DL、DR表示分裂后的左、右数据集结点。
针对股票特征的连续性,采用遍历分裂点的方法计算特征基尼指数。
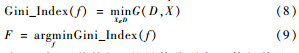
式(8)中,寻找特征f的最佳分裂点X使得其基尼指数值最低,并以该值作为特征f的基尼指数。式(9)中,特征F则是最优的特征。此外,以Gini_Index值为标准便可对特征集合进行排序。
本文采用待预测股票的自身特征数据,使用涨、跌两类标记对每日的股票数据进行分类。图1展示了对中国平安股票6种因子的排序结果。

3 股价行为预测算法
股价行为预测包括每日股价预测和次日股价走势预测。本文提出PRHMM预测模型利用前文进行处理的数据作为输入。该预测模型基于某一只个股的数据,每一只股票对应独立的预测模型。
3.1 股票价格预测
输入的数据为当日股票特征数据集,输出为预测股价。通过已训练的HMM模型计算输入特征数据对应的隐态似然值向量。基于最小二乘估计对相似历史模式进行最优匹配。

其中,i为用于匹配的模式序号;N为隐状态数目;H为历史模式的似然值向量;P为输入数据的似然值向量。
将最优历史模式的次日股价波动值加权累加于当天股票收盘价,即股价预测值。预测算法伪代码如下:

3.2 股票走势预测
将当日股票特征数据作为观测值oT{oT,1,oT,2,…,oT,K},K为股票特征的个数。同时获取前T-1日的对应股票特征数据,封装为观测序列O(o1,o2,…,oT-1,oT)作为输入数据。利用Viterbi算法在训练好的HMM模型上进行状态序列的预测,用对应的次日状态值推测股价的走势方向。图2展示了当K=3时的预测模型原理。
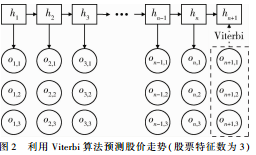
对已知模型λ=(A,B,Π)和观测序列O,需要得到和观测序列匹配概率最高的状态序列H(h1,h2,…,hT),令中间变量初始值分别为δ1(i)={πibi(o1)|i∈[1,C]},Ψ1(i)={0|i∈[1,C]},走势预测算法如下:
(1)递推寻找最优隐状态。对t=2,3,…,T,有:

(2)递推结束求目标隐状态hT值:

(3)根据该状态在历史数据中关于次日股价走势的影响,取比重最大的方向作为预测结果。

4 实验结果与分析
4.1 实验数据
为了测试本文提出的预测模型性能,基于4只A股保险板块股票的历史数据进行实验。不同的股票建立独立的预测模型,由训练集进行特征预处理和模型训练。验证集用于优化参数,如确定模型隐状态数目。模型最终效果的对比分析基于测试数据集。表1展示了实验数据的详细情况。
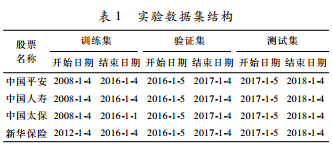
4.2 预测结果与对比
在实验中通过BIC方法得出HMM模型对中国平安、中国人寿、中国太保和新华保险4只股票建立的预测模型隐藏状态分别为7、11、5、4。针对股票价格的预测效果,使用走势准确率和平均绝对百分误差(MAPE)两个指标来衡量。股票价格走势方向分为涨、跌两种,走势准确率为预测次日股价走势方向和真实走势方向相同的次数与预测次数的比值。MAPE是股票价格数值在预测值和真实值之间误差标准,计算公式如下:
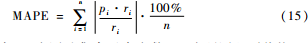
其中,n为测试集合元素个数,pi为预测股票价格,ri为真实股票价格。PRHMM模型在测试集的预测效果见表2。
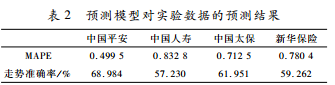
本文提出的PRHMM模型对测试集的预测结果的绝对平均误差是比较小的,走势准确率也高于50%,说明了该模型的有效性。
同时基于同一数据集合,建立对比模型SVM模型和ARIMA模型,对测试集进行预测实验。
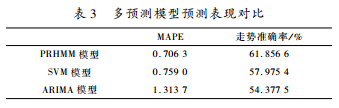
不同种类股票的预测模型,取所有同一类模型计算出的指标平均值作为模型的最终指标值。表3展示了多个模型在同一测试数据的预测效果,可以得知ARIMA模型在测试集上的实验结果波动性大,随机性较强,而SVM模型的结果较为稳定,但相较本文提出的PRHMM模型,其绝对平均误差还是比较大的,且PRHMM模型在股价走势的预测也较传统模型要稳定。
5 结论
本文通过特征工程解决了模型输入因子的问题,设计的特征选择方法使HMM模型中的输入特征更加有效,模型预测的准确率得到提高。此外结合贝叶斯信息准则对模型隐状态数目进行确定,优化模型训练效果的同时防止了过拟合。所提出的PRHMM预测模型在4只A股保险板块的股票进行了预测实验,且在同一数据集结构中,对比了SVM、ARIMA模型,采用MAPE、走势准确率指标来比较预测性能。
实验结果表明,PRHMM模型对选定的测试数据有良好的预测效果。在股价行为的预测上相较SVM模型和ARIMA模型也表现出了更好的效果。同时说明了基于CART的特征选择结合BIC规则确定隐状态数目的方法对于优化HMM模型效果是行之有效的。
在研究过程中,发现对于隐马尔可夫模型的隐状态,不仅其数目影响模型预测效果,其不同状态的意义也可作为股票预测的标准。未来将尝试挖掘隐状态的内涵以用于模型优化和股票交易点分析,并结合神经网络等人工智能算法实现更为稳定的股价行为预测模型。
参考文献
[1] JOSEPH R, MAXWELL S. Commodity futures trading with moving averages[M]. New York: Speer Books, 1975.
[2] KIMOTO T, ASAKAWA K, YODA M, et al. Stock market prediction system with modular neural networks[C]// International Joint Conference on Neural Networks. IEEE, 1990:1-6.
[3] GURESEN E, KAYAKUTLU G, DAIM T U. Using artificial neural network models in stock market index prediction[J]. Expert Systems with Applications, 2011, 38(8):10389-10397.
[4] LUO F, WU J, YAN K. A novel nonlinear combination model based on Support Vector Machine for stock market prediction[C]// Intelligent Control and Automation. IEEE, 2010:5048-5053.
[5] WEIGEND A S,GERSHENFELD N A.Time series prediction:forecasting the future and understanding the past[C]//The NATO Advanced Research Workshop on Comparative Time Series Analysis,Santa Fe,New Mexico:AddisonWesley,1994.
[6] 朱嘉瑜,叶海燕,高鹰.基于隐马尔可夫模型的股票价格预测组合模型[J].计算机工程与设计,2009,30(21):4945-4948.
[7] HASSAN M R, NATH B. Stock market forecasting using hidden Markov model: a new approach[C]. Proceedings of 5th International Conference on Intelligent Systems Design and Applications, 2005. IEEE, 2005:192-196.
[8] HASSAN M R, NATH B, KIRLEY M. A fusion model of HMM, ANN and GA for stock market forecasting[J]. Expert Systems with Applications, 2007, 33(1):171-180.
[9] LIEW C C, SIU T K. Martingale representation and admissible portfolio process with regime switching[J]. Stochastic Analysis & Applications, 2010, 29(1):106-120.
[10] BARAK S, MODARRES M. Developing an approach to evaluate stocks by forecasting effective features with data mining methods[M]. Pergamon Press, Inc, 2015.
[11] DUAN J J, WANG W, ZENG J P, et al. A prediction algorithm for time series based on adaptive model selection[J]. Expert Systems with Applications, 2009, 36(2):1308-1314.
[12] RABINER L R. A tutorial on hidden Markov models and selected applications in speech recognition[J]. Readings in Speech Recognition, 1990, 77(2):267-296.
(收稿日期:2018-03-19)
作者简介:
喻永生(1998-),男,学士,主要研究方向:数据挖掘、机器学习。
张卫东(1968-),男,硕士,副教授,主要研究方向:量化交易。

