0  引言

粒子滤波是一种基于蒙特卡罗思想的非线性非高斯状态估计滤波方法^［1］，在故障诊断、目标跟踪等相关领域取得了一定的应用效果。段琢华等人^［2］提出一种基于粒子滤波器的移动机器人传感器故障诊断方法，并验证了该方法可以有效识别移动机器人一种或多种故障。程建等人^［3］将粒子滤波理论应用于红外目标跟踪，在粒子滤波理论框架下，红外目标的状态后验概率分布用加权随机样本集表示,通过随机样本的Bayesian迭代进化实现红外目标的跟踪。然而随着迭代次数的增加，粒子重要性权重的方差越来越大，使得粒子的权重集中到很少数粒子上，其他粒子的重要性权值将会很小，这就是粒子退化现象。DOUCET A等人^［4］已从理论上证明了粒子退化现象出现的必然性。粒子退化问题将会严重影响粒子滤波精度。

针对粒子滤波存在的粒子退化问题，国内外学者进行了大量的研究。张琪等人^［5］提出一种基于权值选择的粒子滤波算法.按照粒子权值的大小选择较好的粒子用于滤波,以增加样本的多样性,从而缓解粒子滤波的退化问题。夏飞等人^［6］在重采样阶段采用了一种权值排序、优胜劣汰的重采样算法,对各粒子的归一化权值按从小到大的顺序排列，并根据权值方差大小淘汰粒子,从而得到了改进的粒子滤波算法,在一定程度上解决了标准粒子滤波的退化问题。但是上述两种方法仍然是基于传统采样的框架，未能彻底解决粒子退化的问题。

蝴蝶算法(Butterfly Algorithm，BA)是由ARORA S和SINGH S^［7］提出的一种基于蝴蝶觅食行为的全局优化算法。通过仿真指出该算法优于其他自然启发式算法，相较于其他算法具有更高的收敛精度和更快的收敛速度。受此算法特点启发，本文引入蝴蝶算法优化粒子滤波采样过程，并通过仿真实验验证蝴蝶优化粒子滤波算法能够改善基本粒子算法存在的滤波粒子退化问题。

1  粒子滤波算法

粒子滤波是一种基于蒙特卡罗思想的贝叶斯估计方法 ^［8］。假设有非线性系统的状态空间模型:

其中，f(·)和h(·)分别为状态转移方程和观测方程。x_t为系统在t时刻的状态变量，z_t为系统在t时刻的观测值，w_t和v_t为相互独立的噪声，分别为系统的过程噪声和观测噪声，u_t为系统在t时刻的输入量。

滤波就是计算后验滤波概率密度p(x_t|z_1:t)，已知p(x_t|z_1:t)是p(x_0:t|z_1:t)的边沿概率密度。假设t-1时刻滤波概率密度p(x_t-1|z_1:t-1)已知,系统状态x_t服从一阶马尔可夫过程且系统观测z_t独立。通过下式

得出包含t-1时刻观测值的t时刻系统状态先验概率密度p(x_t|z_1:t-1):

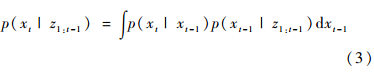
式（3）即为预测过程，其中，p(x_t|x_t-1)是系统的状态转移概率密度。利用t时刻的观测值z_t，通过更新修正p(x_t|z_1:t-1)，得到t时刻系统状态的后验概率密度p(x_t|z_1:t)，由贝叶斯定理可得状态更新方程:

其中

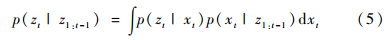
然而，对于非线性非高斯系统而言，在过程中式(3)和式(4)消去中间参量和其他位置参量的计算却很困难，很难得到完整的解析式来表达这样的概率密度函数。因此，粒子滤波采用序贯蒙特卡罗采样方法，从后验概率密度p(x_t|z_1:t)采样大量的随机样本点来近似待估计的分布，这些随机样本点称为粒子。用大量的粒子来近似整个后验分布，当粒子数量足够多时，后验分布能被准确近似，是一种全局近似最优滤波。假设从后验概率密度p(x_t|z_1:t)采样得到N个粒子，则后验概率密度可以通过下式近似表示：

其中，xit表示从后验概率密度中采样得到的粒子，δ(·)表示Dirac delta函数。

但是在实际中却很难从函数p(x_t|z_1:t)中采样。可以先从一个事先已知且容易采样的参考分布q(x_t|z_1:t)中采样，通过在q(x_t|z_1:t)中采样x粒子进行加权来近似计算p(x_t|z_1:t)。当选取重要概率密度为

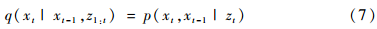
时，重要性权重方差最小，此时为最优重要性概率密度。权值计算方程为:

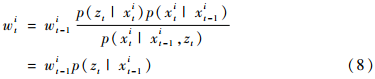
式（8）中，p(z_t|xⁱ_t-1)无法求解，所以更常见的是选取先验概率密度为重要性概率密度，即

式子化简为

将重要性权重归一化，即

而后验概率密度可以表示为：

式中，重要性权值如式(11)所示。当N→∞时，由大数定理可知，式（12）逼近于真实后验概率p(x_t|z_1:t)。

2  蝴蝶优化粒子滤波

2.1 蝴蝶算法

蝴蝶算法是一种自然启发式全局寻优算法，其主要思想类似于蝴蝶群觅食行为，每一只蝴蝶都会散发一定强度的香味，同时每只蝴蝶都会感受到周围其它蝴蝶的香味，并朝着那些散发更多香味的蝴蝶移动。蝴蝶的香味取决于三个因素：感知形态、刺激强度以及幂指数。用方程表示为

F=cI^a(13)

其中，F表示香味浓度大小，c为感知形态，I为刺激强度，a为幂指数。

已知目标函数f(x)，蝴蝶算法的基本步骤如下：

(1)初始化具有n只蝴蝶的蝴蝶种群，由目标函数f(xi)决定每一只蝴蝶xi的刺激强度Ii。

(2)计算蝴蝶种群中每一只蝴蝶的适应值，并找到位置最优的蝴蝶。

(3)计算蝴蝶散发的香味。由于外界环境的干扰，产生随机数p用于决定蝴蝶是进行局部搜索还是全局搜索。

(4)若进行全局搜索，蝴蝶飞向全局适应度最高的蝴蝶，全局搜索可以表示为

其中，xt+1i为第i只蝴蝶在第t次迭代的解向量。g*表示目前所有蝴蝶中的最优解。

(5)若进行局部搜索，蝴蝶进行Lévy随机飞行。局部搜索可以表示为

为了避免蝴蝶移动陷入局部最优，在算法中引入Lévy飞行，Lévy飞行实质是一种随机游走，步长分布符合重尾概率分布：

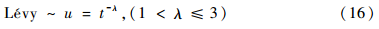
Lévy飞行能够加快局部搜索，提高搜索效率。本文中，λ的取值范围为(1,2］。

2.2  融合蝴蝶算法与粒子滤波

在蝴蝶算法中，把蝴蝶看作粒子滤波中的粒子，可以看出蝴蝶算法和粒子滤波存在一定的相似性。首先，蝴蝶算法中蝴蝶不断地更新自己的位置并向适应度最高的蝴蝶飞去，类似于粒子滤波算法中粒子不断地逼近真实系统状态的后验概率分布。其次，蝴蝶算法中适应度最高的蝴蝶是种群中的最优值，类似于粒子滤波算法中具有最大重要性权重的粒子最可能处于真实的后验分布。

本文将蝴蝶算法优化思想引入粒子滤波采样过程，提高粒子滤波性能。但是如果直接将蝴蝶优化算法与粒子滤波结合，会导致许多的问题，所以引入蝴蝶算法优化粒子滤波的过程中需做如下修改：

（1）常规粒子滤波的重要性概率密度选取的是先验概率密度，丢失了当前时刻的观测值，所以在计算蝴蝶的适应值时利用最新时刻的观测值。因此，计算蝴蝶的适应值方程定义为:

其中，R_k是观测噪声方差，z_new是最新的观测值，z_pred表示预测的观测值。

（2）在蝴蝶的移动过程中，每一只蝴蝶都会向当前已知最优值逼近。而在蝴蝶算法的全局搜索方程中g*-xti已经确定了蝴蝶的移动方向，但是当Lévy飞行出现负值时，蝴蝶却会朝着最优值反方向移动，造成无效的重复计算。因此，应对Lévy飞行取绝对值。改进后的全局搜索方程变为:

（3）在蝴蝶算法的全局搜索方程式(18)和局部搜索方程式(15)中，当Lévy飞行值和Fi值太小时会导致蝴蝶的位置基本不移动，造成无效的位置更新。所以当蝴蝶更新的位移太小时需要根据实际情况进行适当的扩大。

综上，引入蝴蝶算法优化后的粒子滤波(BA-PF)具体实现如下：

(1)初始化。选取先验概率作为重要性概率密度函数，从重要性函数中产生N个粒子组成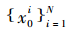粒子群，所有粒子的权值为1/N。设置迭代次数T、搜索切换概率p等参数。

(2)预测。通过式(1)计算状态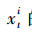的预测值。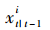

(3)寻找最优值。把粒子滤波中的每一个粒子看作蝴蝶算法中的一只蝴蝶。通过适应度函数式(17)计算每一个粒子的适应度值，并通过式(19)找到全局最优的粒子g*，即适应度值最大的蝴蝶。

(4)利用式(13)计算每一个粒子的香味F_i，产生随机数r用以决定粒子利用式(18)进行全局搜索，或者利用式(16)进行局部搜索。当迭代次数达到最大次数M时，停止迭代。

(5)更新优化后粒子的重要性权重并归一化。

(6)重采样。若有效粒子N_eff小于有效样本阈值N_th，即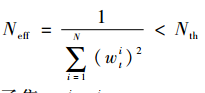时，则进行重采样。得到新的粒子集。

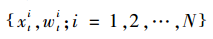(7)状态估计。利用进行状态估计。

(8)判断算法是否继续，若继续，则返回步骤（2），否则算法结束。

3  实验结果及分析

实验硬件环境为笔记本电脑(Intel Core i7处理器、16 GB内存)，实验软件环境为MATLAB 2016a。为了验证改进粒子滤波的有效性，将蝴蝶优化粒子滤波算法(BA-PF)与常规粒子滤波(PF)和基于无迹卡尔曼滤波优化的粒子滤波(UPF)进行对比，本文采用文献［9］中的非线性系统,系统的状态方程和测量方程为:

其中φ1=0.5,φ2=0.2,φ3=0.5,ξ=0.04，过程噪声w取Gamma(3,2)的伽玛噪声，观测噪声v取均值为零、方差为0.000 1的高斯噪声。采用3种算法对上述非线性模型系统状态进行估计和跟踪。采用均方根误差E_RMSE来度量各滤波算法的性能。均方根误差公式为:

实验算法参数设置值参考如表1所示。

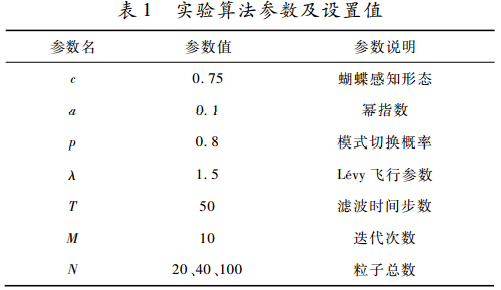
仿真在不同粒子数N=20、N=40、N=100下对三种粒子滤波算法的滤波精度和运行时间进行对比，如表2所示。图1为一次独立仿真条件下粒子数N=20时三种粒子滤波算法的状态估计，图2为对应仿真运行中三种粒子滤波算法的估计误差绝对值。

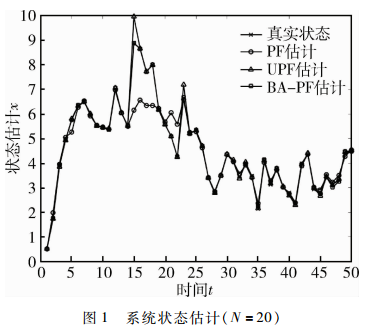
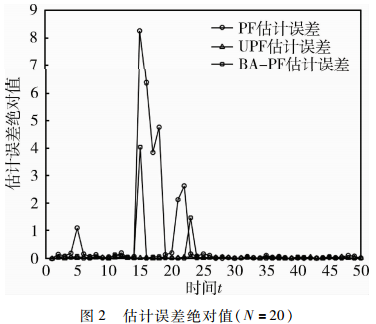
由图1、图2和表2可以看出，BA-PF算法的均方根误差明显小于PF算法和UPF算法，同时BA-PF算法在粒子数较少时就能具有很高的滤波精度，这主要是因为BA-PF算法能够驱动无效粒子向似然概率高的区域移动，增强了粒子的作用效果。而PF算法在粒子数量较少时，容易失去状态估计，如从时间点t=16到t=22。UPF因为引入无迹卡尔曼滤波，所以滤波精度较PF算法有所提高，但是低于BA-PF算法的滤波精度。

为了测试不同粒子滤波算法的鲁棒性，独立仿真在时间点t=40和t=45时刻设置状态发生的突变，幅值为15。图3为粒子数N=20并且发生突变后三种粒子滤波算法的状态估计结果，图4为相应三种粒子滤波算法的估计误差绝对值。从表2中还可知，BA-PF算法的执行时间稍微高于PF算法，但是远低于UPF算法的执行时间。

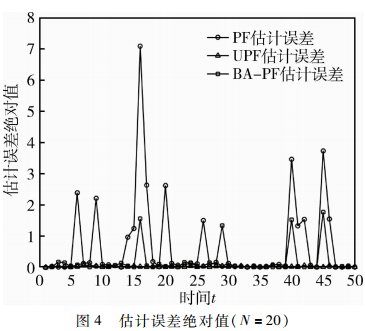
从图3和图4可以看出在t=40和t=45时刻状态值发生跃变，PF算法和UPF算法都发生了明显的估计偏差，其中又以PF算法最为明显。而BA-PF算法由于引入Lévy随机飞行，避免了局部最优问题，没有发生明显偏差，这说明BA-PF算法对系统状态突变的适应性强，算法鲁棒性高。综上，由于BA-PF算法在重要性采样过程中引入蝴蝶优化算法，有效改善了粒子退化现象，提高了滤波精度。

4  结论

本文提出了一种基于蝴蝶优化的粒子滤波算法，引入蝴蝶算法优化常规粒子滤波的重要性采样过程，驱动远离真实状态的粒子向真实状态可能性较大的区域移动，从而有效改善了粒子滤波存在的粒子退化问题，提高了粒子滤波的滤波精度。同时通过蝴蝶搜索模式的切换和Lévy随机飞行使BA-PF算法避免陷入局部最优。实验结果表明，BA-PF算法在粒子数量少量的情况下能实现有效滤波，比PF算法具有更好的滤波性能，算法鲁棒性高。

参考文献

［1］ PARK S, HWANG J P, KANG H J, et al. A new evolutionary particle filter for the prevention of sample impoverishment［J］. IEEE Transactions on Evolutionary Computation, 2009, 13(4):801-809.

［2］ 段琢华, 蔡自兴, 于金霞,等. 基于粒子滤波器的移动机器人惯导传感器故障诊断［J］. 中南大学学报(自然科学版), 2005, 36(4):642-647.

［3］ 程建, 周越, 蔡念,等. 基于粒子滤波的红外目标跟踪［J］. 红外与毫米波学报, 2006, 25(2):113-117.

［4］ DOUCET A, GODSILL S, ANDRIEU C. On sequential Monte Carlo sampling methods for Bayesian filtering［M］. Kluwer Academic Publishers, 2000.

［5］ 张琪, 胡昌华, 乔玉坤. 基于权值选择的粒子滤波算法研究［J］. 控制与决策, 2008, 23(1):117-120.

［6］ 夏飞, 郝硕涛, 张浩,等. 改进粒子滤波在汽轮机故障诊断中的应用［J］. 计算机测量与控制, 2016, 24(1):35-38.

［7］ ARORA S, SINGH S. Butterfly algorithm with Lèvy Flights for global optimization［C］.International Conference on Signal Processing, Computing and Control. IEEE, 2016:220-224.

［8］ GORDON N J, SALMOND D J, SMITH A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation［J］. IEE Proceedings F - Radar and Signal Processing, 2002, 140(2):107-113.

［9］ DOUCET A, FREITAS N D, WAN E. The unscented particle filter［C］. Neural Information Processing Systems, NIPS, 2001: 584-590.

（收稿日期：2018-03-27）

作者简介：

刘云涛（1991-），男，硕士，主要研究方向：嵌入式系统、人工智能。