0  引言

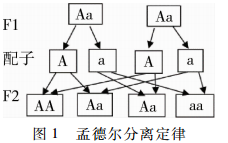
生物学中，二倍体是指含有两个同源基因组的个体^［1］。根据孟德尔分离定律可知，当两个同源基因组其中之一为显性时，该基因对应的性状表现为显性。仅当两个同源基因组均为隐性时，表现型为隐性，如图1^［1］所示。基因重组是保持生物特性世代遗传的基本方式，也是获取大量遗传变异的主要源泉。遗传算法^［2］中的交叉操作可视为对生物遗传过程中基因重组的直接模拟，交叉算子选择得好坏直接影响算法的性能。对于占主流的二值编码（0/1编码）方法来说，目前最常用的交叉方法主要有以下两类：

（1）一点交叉、两点交叉与多点交叉^［1,3-4］

一点交叉（one-point crossover）又叫简单交叉。具体操作是：在个体串中随机设定一个交叉点，实行交叉时，该点前或后的两个个体的部分结构进行互换，并生成两个新个体。

两点交叉（two-point crossover）方法与一点交叉类似，只是多设置了1个交叉点，交叉时，A、B两个体中位于这两个交叉点之间的码串相互交换，其余码串不变。

多点交叉(multi-point crossover) 是前述两种交叉的推广，有时又被称为广义交叉（generalized crossover），一点交叉和两点交叉可视为多点交叉的特殊形式。

（2）一致交叉^［2］

所谓一致交叉（uniform crossover）是指通过设定屏蔽字（mask）来决定子个体的哪些基因继承父本A 中的对应基因，哪些基因继承父本B 中的对应基因。一般来说，点数较多的交叉操作可提供更加丰富的遗传变异材料，有利于维护种群基因型的多样性，但对关键模式的保护能力较差，收敛的速度也较慢。从模式（schemata）处理角度看，一点、两点及多点交叉方法存在着“位置相关”的缺陷。在此情况下，短模长模式比长模长模式有更大的存活概率，而对于很多应用问题，因领域知识较少，基因间的关系密切程度不易确定，人为的基因编码排列方案可能极不合理，这将影响多点交叉操作的效果和GA搜索的效率。

与多点交叉方法相比，一致交叉由于平等对待所有的模式，因而克服了多点交叉方法存在的“位置相关”缺陷，但在种群基因型相似性较高的情况下，由于随机交换发生在相同基因座之间的概率较高，故存在优化后期阶段进化迟钝、搜索效率欠佳的缺陷。

针对上述问题，参照生物DNA遗传机制机理，提出并研究设计了一类拟合生物遗传二倍体显性机制的新型DNA遗传算法。

1  二倍体显性遗传算子

一点交叉、多点交叉及一致交叉方法的共同之处在于均继承了两父串的相同基因，差异仅在于对父串不同基因的处理方式。二倍体显性遗传算子也可以继承亲本同型等位基因，而对杂型等位基因则按“与”和“或”逻辑分别进行处理。例如，若两父串为：

F1: 0100101101

F2: 1101110100

则由“与／或”交叉方法产生的两子串分别为：

C1: 0100100100

C2: 1101111101

显然，这一遗传操作方法使子代继承了双亲的同型基因；对于双亲的杂型基因，“与／或”交叉方法采取了两种不同的“强调”策略：“与”运算强调0基因的作用，而“或”运算则强调1基因 的作用。这种交叉方法较为逼真地模拟了生物DNA遗传的显性(dominance)机制，“与”运算将1视为隐性基因，而“或”运算将0视为隐性基因。

2  二倍体显性遗传计算模式分析

为便于对AO交叉方法进行模式分析，这里参照Holland模式分析方法，先定义几个有关基因型模式的概念。

定义1： 0_模式由字符集{*0*}构成的字符串称作0_模式，记为H0。其中，字符0为反映模式结构特征的确定性信息，*为反映模式结构特征的不确定性信息。

定义2： 1_模式由字符集{*1*}构成的字符串称作1_模式，记为H1。其中，字符1为反映模式结构特征的确定性信息，*为反映模式结构特征的不确定性信息。

有了这些定义，再参考 Holland模式分析方法^［1,3-4］，不难得出二倍体显性遗传计算在模式形成和增长方面具有如下特性：

（1）1阶优模式的数目（数学期望）在连续后代中按式(1)增长：

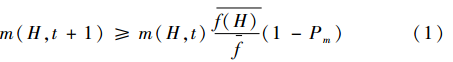
（2）高于种群的平均适应度的1阶0_模式在连续后代中按式(2)增长：

（3）高于种群的平均适应度的1阶1_模式在连续后代中按式(3)增长：

其中，H表示某个模式，m(H,t)表示在t代种群中隐含模式H的串的个数，m(H,t+1)表示在t+1代种群中隐含模式H的串的个数（数学期望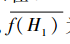），为t代种群中含模式H个体的平均适应度，f为t代种群中所有个体的平均适应度，Pm为变异概率，ο(H)为模式H的模阶。

很明显，与 Holland标准GA相比，基于二倍体显性机制的DNA遗传计算（AO交叉）对于适应度高于种群平均适应度的0_模式和1_模式有较强的保护能力。而对于0、1混杂的一般模式，AO交叉方法对模式H的破坏作用除了与变异概率以及模阶的高低相关外，还与模式H中的0和1个数之比相关。当模式H中0和1个数相等时，AO交叉对模式H的破坏作用最大。

模式H中0和1在数目上相差越大，AO交叉对模式H的破坏作用越小；当模式H中的确定信息位全为0或全为1时，AO交叉对模式H无破坏作用。由此不难推测AO交叉操作在搜索、优化应用中可能具有如下特点：

（1）当问题全局最优解的基因编码为全0或全1时，由于AO交叉对0_模式和1_模式无破坏作用，因此，采用AO交叉的GA可能会以相当高的速度搜索到问题的全局最优解。

（2）当问题全局最优解的基因编码0、1个数在数量比上相差很大时，由于AO交叉对这类0、1混杂优模式破坏作用较小，因此，与一点交叉等方法相比，采用AO交叉的GA可能会以相对较快的速度搜索到问题的全局最优解。

（3）当问题全局最优解的基因编码0、1个数在数量比上相差不大直至相等时，由于AO交叉对这类0、1混杂优模式破坏作用较大，此时，采用AO交叉的GA的收敛可能比较慢，甚至不及一点交叉或一致交叉等方法。

3  遗传优化实验

为了检验AO交叉方法的优化性能，本文选择了易于采用 0/1二值编码方案的典型优化问题进行实验，即Bohachevsky函数优化问题。

实验环境为：Inter(R) Core(TM) i5-7300U CPU @2.6 GHz 2.71 GHz笔记本电脑，Windows 10，Visio Studio 2010。

Bohachevsky函数^［5-7］为：

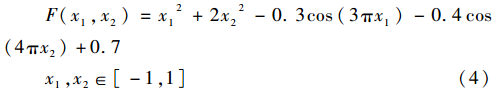
优化目标为求Bohachevsky函数的全局最小值。由数学分析方法可知Bohachevsky函数的最小值为0，发生在(0,0)点。该函数三维形状如图2所示。

实验目的在于检测AO交叉方法的性能，选用一点交叉作为比较对象，GA的配种选择机制采用正比于适应度的赌轮随机选择方式。为了与AO交叉法的逻辑操作形式相一致，这里的变异操作采用“异或/异或非”方式，其效果等同于位点变异方法。实验中的变异概率为0.05，交叉概率为1.00，种群规模为400，种群更新方式采用最佳保留方式。采用二进制编码方式，实验结果如表1所示，表中列出的优化时间为20次实验的平均值。

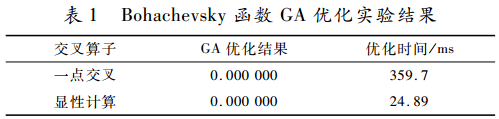
从实验结果可以看出各种不同的交叉算子在Bohachevsky函数优化中均能搜索到全局最优解但优化效率有差异。AO 交叉操作方法在优化效率方面明显高于一点交叉方法。根据前文对AO交叉方法的分析，AO交叉的优化性能可能还与问题最优解的编码特性（0和1的数量比）相关。为此，本文通过设置最小极值点发生的位置来改变取得最优解时自变量编码的0和1的个数。为检测最优解的编码特性对AO交叉法优化性能的影响，令：

          x₁=y₁－m                      (5)

           x₂=y₂－m                      (6)

这样，如果针对自变量y1、y2进行遗传优化，则Bohachevsky函数的最小极值点发生在(m,m)。实验中，y1、y2的编码方式为二进制编码方式，位长均为30位。适应度函数设计为：

           f（x₁,x₂）=1/（F（x₁,x₂）0.000 001）   (7)

为了调整最优解的编码特性，本文将m线性映射到30位二进制编码空间，00…00对应于 -1.00,11…11对应于+1.00；实验中的其他参数设计与前述Bohachevsky函数优化相同。实验结果表明，采用AO交叉法的GA算法能搜索到Bohachevsky函数不同位置的全局最优解，但优化所需时间有较大差异。图3显示了不同m值下， AO交叉法的优化时间曲线，其中，纵坐标为优化到最优解所需的时间（20次实验的平均值），横轴为m在二进制编码中所含0的个数，自0直到30。

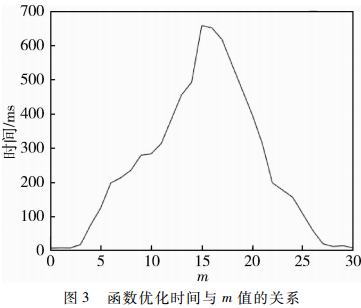
从图3可以看出，AO交叉方法的优化效率随着0、1数目的变化有很大差异；在m值（二进制码）为00…00和11…11时，AO交叉方法的优化效率最高，而当m中的0、1个数比接近于1时，AO交叉的优化效率最低。

4  结束语

与流行的一点交叉和一致交叉等方法相比，本文提出并研究设计的二倍体显性DNA遗传计算方法在模式抽样机理方面有其独特性，主要表现在对优质0_模式和优质1_模式有较强的保护作用。实验结果显示，这种抽样特性导致AO交叉的优化效率随最优解（二值编码）的0、1分布变化而发生变化；最优解包含的0和1的个数相差越大，则优化效率越高，反之，则优化效率越低。实验结果也显示出在最优解包含的0和1的个数之比接近于1.00的较小范围内，AO交叉方法的优化效率较低。如果假定最优解所包含的0（或1）个数呈均匀分布，则AO交叉方法将在总体优化效率上明显超越一点交叉等传统遗传算法，统计实验结果有力支持了上述理论分析与算法设计思想。

需要特别指出的是，生物DNA遗传过程除了多倍体显性机制机理外，还特别依赖于DNA双螺旋结构。生物DNA双螺旋二倍体染色体结构在群体遗传基因多样性维护方面有着独特的功效。限于篇幅，有关二倍体双螺旋结构的DNA模拟计算研究在此不做赘述。

参考文献

［1］ GLODBERG D E.Genetic algorithms in search, optimization & machine learning［M］.Addison-Wesley, Reading, Mass, 1989.

［2］ Peng Hu,Wu Zhijian,Zhou Xinyu, et al.Dynamic differential evolution algorithm based on elite local learning［J］.Acta Electronica Sinica,2014，42 (8) : 1522-1530.

［3］ 鲁宇明,黎明,李凌.一种具有演化规则的元胞遗传算法［J］.电子学报,2010,38 (7) : 1603-1607.

［4］ 刘渊,杨永辉,张春瑞,等. 一种基于遗传算法的Fuzzing测试用例生成新方法［J］.电子学报,2017,45(3):552-556.

［5］ FOGEL G, FOGEL D.Continous evolutionary programming:analysis and experiments［J］.Journal of Cybernetics and Systems,1994,26（1）:79-90.

［6］ 李柱.基于自适应遗传算法的软件测试用例自动生成［J］.计算机系统应用,2016,25(1):192-196

［7］ 陈贤富, 庄镇泉,王煦法.遗传算法的自适应进化策略及TSP问题的遗传优化［J］. 电子学报, 1997,25 (7):111-114.

（收稿日期：2018-04-11）

作者简介：

徐凯（1991-），女，硕士研究生，主要研究方向：深度学习与人工智能。

陈贤富（1963-），男，副教授，主要研究方向：复杂系统与计算智能。