文献标识码: A
DOI:10.16157/j.issn.0258-7998.182545
中文引用格式: 张莹莹. 基于三次样条函数的加Rife-vincent自卷积窗插值FFT算法的电力系统谐波检测[J].电子技术应用,2018,44(10):171-173,178.
英文引用格式: Zhang Yingying. Power system harmonic detection based on cubic spline function and Rife-vincent self-convolution window interpolation FFT algorithm[J]. Application of Electronic Technique,2018,44(10):171-173,178.
0 引言
电力系统中非线性负荷的大量增加,特别是电力电子装置的广泛应用,使电网中产生大量的谐波与间谐波,从而严重影响了电能质量,对电力系统的安全与经济运行造成极大的影响[1]。因此,准确测量电网中的谐波信号,实时掌握电网中的谐波参量,对防止谐波危害,维护电网的安全运行是十分必要的[2]。
目前电力系统谐波分析的主要方法有模拟滤波器法[3]、小波变换法[4]、神经网络法和快速傅里叶算法(FFT)[5]。相较于前几种方法,快速傅里叶算法(FFT)易于在ARM、DSP等嵌入式系统中实现,计算速度快、效率高、技术成熟[5],因此FFT谐波检测法应用最多。
在同步采样下,对谐波信号运用FFT算法检测,能准确得到谐波信号参数。而对电网中的动态信号即使采用频率跟踪技术,也很难做到严格地同步采样。在非同步采样下运用FFT对信号进行参数检测时,非同步采样与数据截断所引起的频谱泄漏和栅栏效应造成的误差较大。针对谐波检测中FFT检测法的栅栏效应和频谱泄漏问题,加窗插值是消除栅栏和抑制频谱泄漏的有效方法。经典窗有Hanning窗[6]、Blckman-Harris窗[7]等余弦窗。Hanning窗的特点是插值公式较简单,而且计算量小,但是分析精度较低;Blckman-Harris窗插值FFT算法的特点是分析精度较高,但是插值公式过于复杂,且计算量大,因而使用不便。本文在分析 Rife-Vincent 窗频谱特性的基础上,提出了基于三次样条函数的加Rife-vincent自卷积窗插值FFT算法。卷积窗在幅值和频率检测方面有较高的谐波检测精度。通过Rife-vincent自卷积窗对采样信号进行加权截断,可有效抑制频谱泄漏,减少谐波间的相互干扰,进一步提高信号参数检测的准确度,并且通过三次样条函数,有效地消除了栅栏效应。通过MATLAB软件,对含谐波的信号进行检验仿真,验证了本文所提的算法能够对谐波信号进行精确分析。
1 基于三次样条函数的加Rife-vincent自卷积窗插值FFT算法
Rife-Vincent自卷积窗具有优良的旁瓣性能,采用Rife-Vincent自卷积窗能够有效抑制频谱泄漏,减少谐波间的相互干扰,通过使用三次样条函数对Rife-Vincent自卷积窗加权截断后的信号进行分析,能够准确得到各谐波信号的参数。
以频率为fh、幅值为Ah、初相位为φh、最高谐波次数为h的谐波信号x(t)为例:


此嵌套形式的三次样条插值算法的形成过程如下:
(1)δ在区间[0,1]等步长取11个插值点(αi,δi),(αi+1,δi+1)…;
(2)取三次样条插值函数的边界条件为自然边界条件;
(3)调用MATLAB中的spline函数分段拟合出10段三次样条插值函数(分段越多拟合精度越高);
(4)通过以上3步求得三次样条函数;
(5)离线求出式(8)所示嵌套形式的三次样条插值函数。

2 仿真分析
为验证本文所提算法的有效性与准确性,选用弱谐波信号进行仿真,仿真模型如下:

其中基波信号频率f0=50 Hz,采样频率fs=1 500 Hz,窗函数长度N=2 048,各次谐波信号的幅值与相位如表1所示,其中相位为本文给出的初值。仿真结果如表2、表3所示。


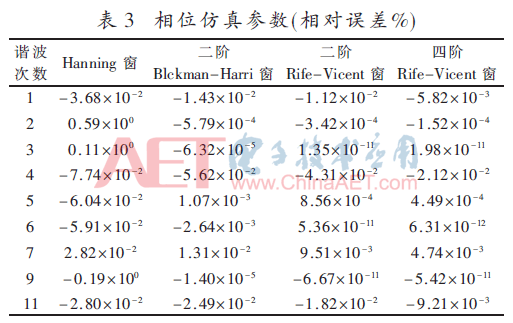
从表2、3中可以看出:
(1)与直接FFT运算相比,加窗插值FFT算法大大提高了谐波检测精度;
(2)随着窗函数的旁瓣衰减速度的加快、旁瓣峰值的降低,抑制频泄露能力得到提高,信号检测精度提高;
(3)较经典窗相比,卷积窗在幅值和频率检测方面进一步提高了谐波检测精度;
(4)由于p阶Rife-Vincent自卷积窗优越的旁瓣性能,二阶Rife-Vincent自卷积窗的谐波检测精度较二阶Nutall自卷积窗检测精度有所提高,以五次谐波和八次谐波为例,二阶Rife-Vincent自卷积窗的谐波检测精度较二阶Nutall自卷积窗在幅值方面相对误差最大可降低0.1%,相位检测相对误差最大可降低0.1%;
(5)随着Rife-Vincent自卷积窗卷积阶数p的增加,检测精度也有所提高,相对误差大约降低了0.1%,特别是四阶Rife-Vincent自卷积窗在三次、六次和九次谐波,检测结果非常接近真实值。
3 结论
采用FFT算法对电力系统谐波分析时,由于频谱泄漏的影响,使得谐波参数的检测有较大的误差。为减小频谱泄漏的影响,本文选用旁瓣性能优越、时域结构简单的四项一阶Rife-vincent窗作为母窗,构造p阶Rife-Vincent自卷积窗。与经典窗、经典自卷积窗相比,本文所选用的p阶Rife-Vincent自卷积窗旁瓣峰值低、旁瓣衰减速度快,能够有效抑制频谱泄漏,减少谐波间的相互干扰,提高谐波检测精度。采用三次样条函数逼近幅值比公式,避免解高次方程,简化了计算,有效地消除了栅栏效应。通过仿真结果可以看出,本文所提的基于三次样条函数的加p阶Rife-Vincent自卷积窗插值FFT算法,在弱谐波信号检测中,能够有效提高检测精度,准确检测谐波参数。
参考文献
[1] 刘冬梅,郑鹏,何怡刚,等.几种谐波检测加窗插值FFT算法的比较[J].电测与仪表,2013,50(12):51-55.
[2] 牛胜锁,梁志瑞,张建华,等.基于四项余弦窗三谱线插值FFT的谐波检测方法[J].仪器仪表学报,2012,33(9):2002-2008.
[3] 牛胜锁,梁志瑞,张建华,等.基于三谱线插值FFT的电力系统谐波分析[J].中国电机工程学报,2012,32(16):130-136.
[4] 张鹏,李红斌.一种基于离散小波变换的谐波分析方法[J].电工技术学报,2012,27(3):252-258.
[5] 温和,滕召胜,郭斯羽,等.Hanning自卷积窗函数及其谐波分析应用[J].中国科学E辑:技术科学,2009,39(6):1190-1198.
[6] 高索丹,巴鹏.Hanning窗在电力系统谐波分析中的应用[J].自动化技术与仪表,2008,27(11):124-127.
[7] 赵文春,马伟明,胡安.电机测试中谐波分析的高精度fft算法[J].中国电机工程学报,2001,21(12):83-87.
[8] KINCAID D,CHENEY W.数值分析[M].王国荣,俞耀明,徐兆亮,译.北京:机械工业出版社,2005.
[9] 孙同明,许珉,杨育霞.应用三次样条函数快速计算插值FFT算法[J].电力自动化设备,2007,27(6):60-62.
作者信息:
张莹莹
(河南省信阳市质量技术监督检验测试中心,河南 信阳464000)

