0 引言

    声源定位技术是阵列信号处理的关键技术之一，它在视频会议、语音识别、说话人识别和助听设备等领域中都有广泛的应用，是语音信号处理领域中一个新的研究热点。目前，基于麦克风阵列的声源定位方法大体上可分为三类：基于到达时延(TDOA)的定位技术^[1]、基于可控波束形成的定位技术^[2]、基于子空间的定位技术^[3]。

    基于子空间的声源定位技术来源于现代高分辨率谱估计技术，其中多重信号分类(Multiple Signal Classification，MUSIC)是一种经典的子空间定位法，在特定的条件下具有很高的估计精度和稳定性等良好性能，本文结合麦克风阵列远场信号的特点，对其进行深入的分析，将传统的MUSIC算法进行改进，使其适用于麦克风阵列的声源定位^[4]。

1 MUSIC声源定位算法分析

1.1 传统MUSIC算法

    MUSIC算法是一种经典的超分辨DOA估计算法，它是在窄带信号源的假设情况下提出来的，其主要思想是对阵列输出数据协方差矩阵进行特征分解，得到与信号分量相对应的信号子空间和与信号分量相正交的噪声子空间，再利用信号子空间和噪声子空间的正交性，构造出非常尖锐的“针状”空间谱峰，通过谱峰的搜索，从而实现信号的DOA估计^[5]。下面针对远场窄带信号模型，简要介绍传统MUSIC算法的基本原理及其计算步骤。

    (1)假设空间有D个远场窄带信号源，分别入射到M元阵列上，其中信号源则整个阵列的接收信号为：

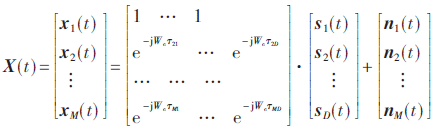
    由式(6)可知，与谱峰所对应的角度就是波达方向的估计值，即在真实波达方向的附近出现非常尖锐的“针状”空间谱峰。

    在实际应用场合中，麦克风通常处理的是宽带非平稳语音信号，而传统的MUSIC算法是在窄带平稳信号的假设基础上提出来的，除此之外，由于多径信号传输现象，使得相干声源普遍存在^[6]，从而导致定位性能较差，精度不高。因此需要对传统的MUSIC算法进行必要的改进，以适用于麦克风阵列的声源定位。

1.2 改进的MUSIC声源定位算法

    本文针对麦克风接收信号为宽带信号且存在相干源这一特点^[7]，采取把宽带信号在频域上分成N个带宽较小的子带来处理。假设一帧信号的频率范围为[f_L，f_H]，则每一个子带对应的频率范围为{[f₁，f₂]，…，[f_k，f_k+1]，…，[f_N，f_H]}，再根据宽带聚焦算法对每个子带信号进行处理。宽带聚焦算法的基本思想是通过聚焦矩阵将频带内不重叠的各频率点的数据转变成参考频率点的数据，得到聚焦后的协方差矩阵，然后再利用传统的MUSIC方法进行DOA估计^[8]。其关键就在于聚焦矩阵的选择，本文采用的是双边相关变换（TCT）算法。

    双边相关变换算法是利用频带内各频率点间无噪声数据之间的关系来选择聚焦矩阵。假设T_β(ω_j)为聚焦矩阵，其中β是真实信号的预估计方向。则有：

    从式(15)可以看出，权向量W_SNR与该子带的总平均功率成正比。那么式(14)可以写成：

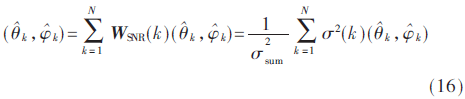
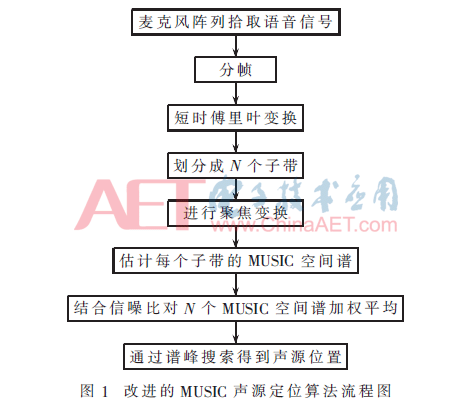
    由于在短时间内语音信号可以看作是近似平稳的，因此可以采取对接收信号进行分帧和短时傅里叶变换的方法来解决语音信号的非平稳性问题^[10]。这样即可提高定位性能，减少噪声对估计结果的影响。综上所述，改进的MUSIC声源定位算法具体实现流程如图1所示。

2 实验仿真分析与比较

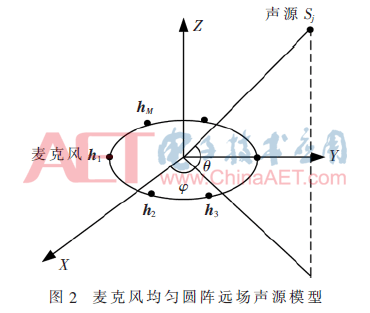
2.1 远场信号模型的建立

2.2 实验环境和参数设置

    本实验在图2所示的均匀圆形阵列远场声源模型的条件下进行，选取25个全向麦克风，采用3个语音信号源，均为标准的英文诵读，采样频率为16 kHz，采样精度为16 bit。噪声为全向高斯白噪声，为了保证其短时平稳性，先将阵列采集数据进行分帧加窗短时傅里叶变换，帧长为512点（32 ms），帧移为256点，俯仰角θ的搜索范围为0~90°，方位角的搜索范围为0~180°，θ角和角的搜索步长为1°。

2.3 性能分析与比较

    为了更好地验证改进MUSIC算法的性能，采用空间谱及其等高曲线图来表示定位结果的精确性。设定信噪比SNR=8 dB，子带数N=12，3个声源信号的俯、仰角各为[θ₁，₁]=[30，30]，[θ₂，₂]=[40，50]，[θ₃，₃]=[60，50]，两种定位算法的仿真结果如图3、图4所示。

    空间谱峰的极值点对应声源的位置，图5和图6分别为两种算法的空间谱等高曲线图、中心点对应声源位置。

    从仿真结果可以看出，传统的MUSIC算法仅能估计出2个声源的位置，而改进的MUSIC算法可以清晰地估计出3个声源的位置，相对传统MUSIC算法而言，其峰值尖锐程度和定位精度都有显著提高，其定位性能和实时性得到改善。

    下面再从俯仰角和方位角的均方差来对这两种算法的定位性能进行分析，信噪比为-10 dB~10 dB，利用阵列采集的所有数据独立试验50次，得到其均方误差如图7所示。

    从俯仰角和方位角的定位均方误差曲线可以看出，在低噪声的情况下，两种定位算法的性能相差不大，但在高噪声环境下，传统MUSIC算法的定位效果则明显变差，从而验证了改进的MUSIC算法抗干扰性较强，其定位性能及精度远远优于传统的MUSIC算法。

3 结束语

    传统的MUSIC算法仅对窄带平稳信号有效，且抗干扰能力较差，定位精度较低。改进的MUSIC算法采取分帧和短时傅里叶变换的方法来解决语音信号的非平稳性问题；针对麦克风接收信号为宽带信号且存在相干源这一特点，改进的MUSIC算法采取把宽带信号在频域上分成N个带宽较小的子带，并将信噪比（SNR）和性能结合起来考虑，采用基于信噪比的加权法来进行定位处理。通过理论分析和实验仿真结果表明，对传统的MUSIC算法进行改进和扩展，得到改进的MUSIC算法在低信噪比情况下，仍能准确地分辨出多个比较接近的声源信号，且算法稳健，定位精度较高，从而验证了该算法具有较强的抗噪声能力和较高的空间分辨率。

参考文献

[1] 王红军.基于TDOA定位GSM移动台的信号处理算法[J].电信技术，2011，51(7)：55-59.

[2] 王志峰，冯杰，蒋灏，等.基于SRP和GA的声源定位方法[J].电声技术，2013，37(10)：36-40.

[3] 王磊，吴仁彪，卢丹.基于子空间技术的常规多波束形成抗干扰算法[J].华东理工大学学报（自然科学版），2011，37(3)：372-376.

[4] 苏永振，袁慎芳，王瑜.基于多重信号分类算法的复合材料冲击定位[J].复合材料学报，2010，27(3)：105-110.

[5] 赵谦，董民，梁文娟.DOA估计算法的一种修正MUSIC算法的研究[J].计算机工程与应用，2012，48(10)：102-105.

[6] 曾光，赵乐军.室内无线高精度定位的改进MUSIC算法[J].华东理工大学学报(自然科学版)，2014，40(5)：614-618.

[7] MARINESCU R S，BUZO A，CUCU H，et al.New considerations for accumulated ?籽-cross power spectrum phase with coherence time delay estimation[C].The Eighth International Conference on Digital Telecommunications，2013：45-48.

[8] 王进，赵拥军，王志刚.一种新的宽带DOA估计自聚焦算法[J].计算机工程与应用，2008，44(29)：57-60.

[9] 周生华，刘宏伟，刘保昌，等.信噪比加权空间分集雷达目标检测算法[J].西安电子科技大学学报(自然科学版)，2011，38(4)：82-88.

[10] 张奕，孟书杰.针对头佩式麦克风阵列的声源定位算法研究[J].计算机工程与应用，2015，51(24)：266-270.

作者信息:

邓艳容，李嘉栋，张法碧，罗  迪，朱承同，冯振邦

(桂林电子科技大学 广西精密导航技术与应用重点实验室，广西 桂林541004)