0 引言

    气候变化对人类的生产生活、政治经济、科技等方面影响巨大。地球系统模式（Earth System Models，ESMs）是基于动力、物理、化学、生物过程及其相互间的能量物质交换构建的一系列数学物理模型，是预测未来气候变化的重要工具^[1]。模式中含有大量取值不确定的参数，会极大影响地球系统模式的模拟性能^[2]。然而随着模式发展，不确定参数越来越多^[3]，这导致参数不确定性分析难以实施。其原因一方面是参数空间随着参数数量增加呈指数增长，计算成本不可接受；另一方面是由于地球系统模式强非线性，参数间存在复杂的交互关系。因此，通过筛选重要参数来减少待研究参数个数是参数不确定性分析的重要步骤，是提高地球系统模式模拟性能的关键。

    参数敏感性分析方法（Sensitivity Analysis，SA）是一类传统的参数筛选方法^[4]。其中基于方差分解的Sobol′方法应用普遍，许多研究表示它是一个里程碑，能提供最准确和鲁棒的结论^[5-6]。然而传统SA并没有考虑随着不敏感参数的剔除，参数敏感性信息不断改变^[7]，这有可能导致参数筛选结论不可靠。

    本文首先验证了这种筛选偏差的存在，其次提出了动态敏感性分析方法(Dynamic Sensitivity Analysis Method，DSAM)。它利用全连接的超图结构存储参数的敏感性信息，将参数筛选问题转换为最密子图的识别问题。最后将DSAM应用于两个模型：一般非线性数学函数、单柱大气模式。通过对比，验证了DSAM比传统Sobol′方法能更有效地识别重要参数。

1 传统敏感性方法的参数筛选问题

    本文利用Ishigami函数进行两次敏感性分析，结果如图1所示。第一次扰动全参数集，它的结果是传统Sobol′的筛选结果。第二次固定不敏感参数x₃不变，只对剩余参数子集进行扰动，使有关x₃的交互敏感性消失，最敏感的参数会变为x₂。这说明参数筛选过程中非敏感参数的剔除会通过交互作用动态影响到其他参数的敏感性。

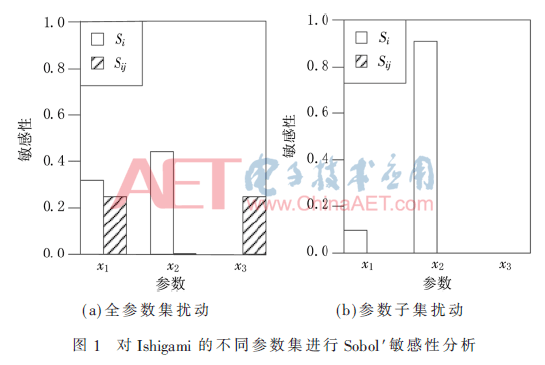
2 动态敏感性分析方法

2.1 敏感性超图构建

    敏感性超图是一个全连接、权重全为正实数且含超边的图。超边代表连接两个以上节点的边。节点代表参数，点权代表主敏感性，边权代表交互敏感性，超边权代表二阶以上的高阶交互敏感性。实际高于二阶的交互敏感性太小可以忽略^[9]，因此本文只计算二阶交互敏感性。

    基于方差分解(如式(2)所示)可计算传统Sobol′方法的三类敏感性和参数组合的组合敏感性(如式(6)所示)。显然全参数的组合效应接近1。

2.2 最密k阶子图搜索

    给定子图中节点数量k，最密k阶子图就是其中权重最大的子图。本文基于深度优先搜索算法(Depth-First-Search，DFS)递增式搜索最密子图，即k从1递增到n-1过程中，对每个k值进行一次k阶最密子图的搜索。递增式搜索的停止条件是当前k阶最密子图的权重接近原始图的总权重，如80%。由于敏感性超图的总权重为1，因此停止标准可设置为0.8。

3 实验设计与分析

3.1 实验模型

3.1.1 数学函数

    Moon10hd是一个含有20个参数的高维非线性函数^[10]，如式(7)所示。它含有线性项、二次指数项和二阶交互项，其中θ(x_i)中含有大量的小系数项。本文利用Moon10hd的100 000个样本进行分析。

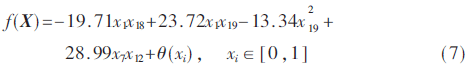
3.1.2 单柱大气模式

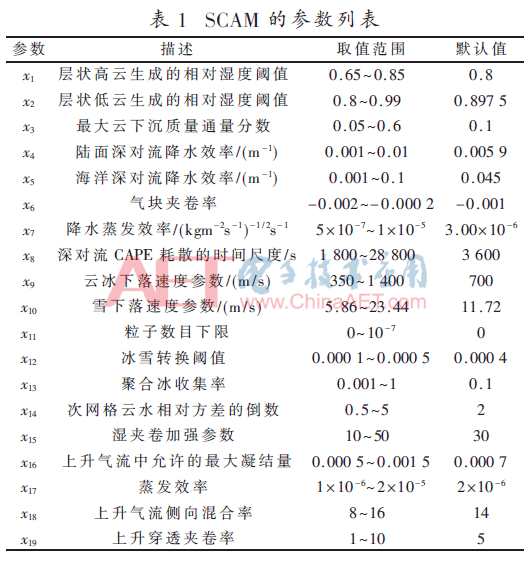
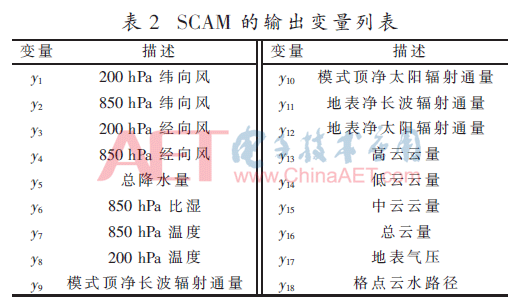
    单柱大气模型（Single-column Community Atmosphere Model，SCAM）用于模拟一个网格点的大气物理过程^[11]。本实验限制网格点在澳大利亚北部，模拟时间是从2006年1月18日至2月13日。观测资料来源于该地区6个无线电探空站每3小时收集到的观测数据。参数和输出变量见表1、表2。模式结果如式(8)所示，代表N个输出变量与观测的平均偏差。本文利用了SCAM模拟的10 000次样本。

3.2 参数筛选结果评估方法

    本文利用传统Sobol′与DSAM的筛选结果进行对比。变量wDiff(Weighted Difference)用于量化评估参数筛选结果的差异。当差异小于0.01 时可视为敏感性指标不变，所以当wDiff低于1% 时，可认为两个筛选结果近似相同。

    参数筛选要为后续参数不确定性分析（如参数取值优化）提供待研究参数。当固定待优化参数的数量时，对更敏感参数调优更有可能达到更佳的优化效果。协方差矩阵适应演化策略(CMA-ES)是一类经典的优化方法。本文分别将Sobol′和DSAM的筛选结果应用于CMA-ES调优，若优化后模式结果越低，筛选结果越有效。

4 实验结果

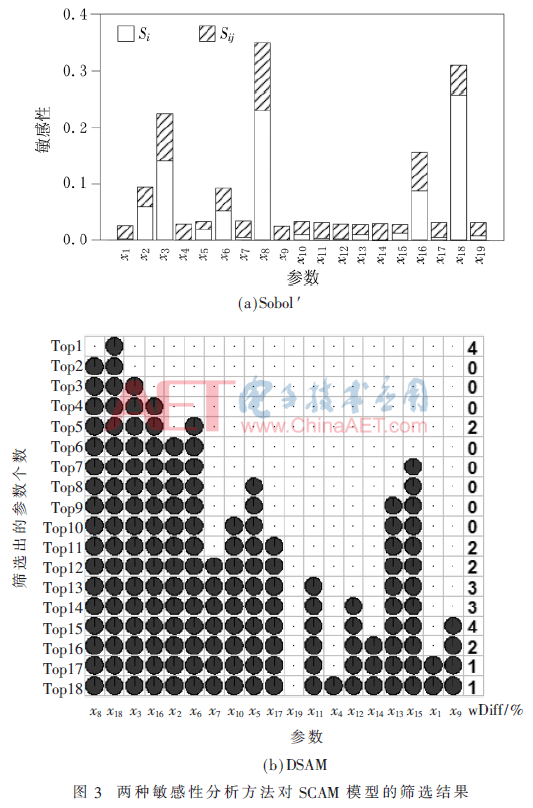
    图2(a)和图3(a)显示了传统Sobol′方法对Moon10hd函数、SCAM模式的参数敏感性结论，总敏感性最高的参数被筛选出来。图2(b)和图3(b)展示了DSAM的动态筛选结果。每列代表一个参数，从左到右按Sobol′的结果递减地排序，实心表示参数被筛选出来，筛选出的敏感参数个数随行号递增。最后一列是传统Sobol′方法和DSAM筛选结果的量化差异(即式(9))。

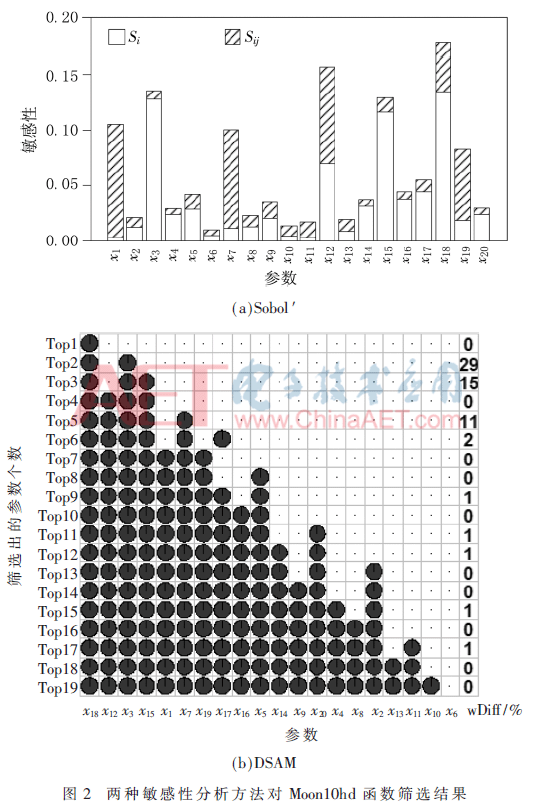
    即使两个筛选结果的组成成员大部分相似，加权差异也可能很大。对于Moon10hd的最敏感的两个参数(如图2(b)所示)，Sobol′和DSAM的筛选结果的量化差异高达29%，而对于前3位敏感参数，筛选差异也超过10%。

    Sobol′和DSAM的筛选结论的不一致有助于发现潜在的关键过程。文献[12]认为x₁₂是Moon10hd函数中的关键参数，而它甚至没有出现在前3的敏感参数中。对于SCAM模型，Sobol′剔除掉的不敏感参数x₁₃和x₁₅被DSAM识别为敏感。从物理意义上分析，x₁₃(聚合冰收集率)影响冰的反射率，进而影响关键的辐射过程。x₁₅(湿夹卷加强参数)影响底部湍流，而x₁₉(上升穿透夹卷率)代表更高层的湿气夹卷，较低位置的湍流过程更为重要。

    图4、图5分别显示了对DSAM和Sobol′的筛选结果进行优化后的模型结果，其中每个都分别选择了大量参数集合和少量参数集合。首先，当优化更多参数时，模式结果的优化程度更好，而调优过程越不容易收敛。其次，相比Sobol′，DSAM的筛选结果能使结果收敛到更优解，即相对于观测的偏差更小。由图4可知，DSAM识别到的Top2敏感参数的调优效果比Sobol′的结果提升了38.5%，而所需迭代次数减少了26.6%。同样，对于Top5重要参数，优化效果提升了12.5%，迭代次数减少了36.1%。

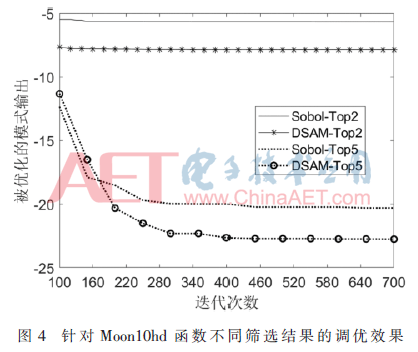
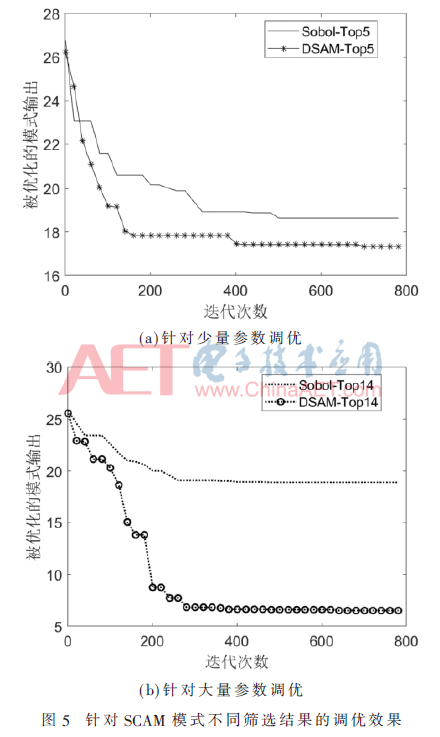
    尽管只有少量参数不同，但参数调优中优化效果差别却可能很大。在图5(b)中，14个参数中只有2个发生了替换，即x₄和x₁₉替换为x₁₃和x₁₅，但调优效果提升了65.2%。

    因此，无论从量化比较还是基于参数调优应用的评估，都证明了DSAM比传统Sobol′更为有效。

5 结论

    本文基于一个经典数值函数说明了参数交互作用对参数筛选过程的影响，提出了一个基于动态敏感性的筛选算法(DSAM)，并在两个测试案例中，分析对比了DSAM和传统筛选方法的效果。通过实验和分析，可得到如下结论：

    (1)参数交互作用在模式参数筛选过程中动态变化，对筛选结果有很重要的影响作用。参数筛选实际是一个组合优化问题。 

    (2)DSAM算法利用图结构来存储参数敏感性信息，将参数筛选问题转换为递增式搜索最密子图问题。由于保证了动态性，从理论上DSAM更适合参数筛选应用。

    (3)实验表示相比传统方法，DSAM的筛选结果量化差异可高达29%。这表明基于组合最优和单一敏感性指标的结论差异很大。

    (4)针对参数调优应用，即使筛选结果的组成差异很小，带来的调优效果差异可高达67%。

参考文献

[1] 王斌，周天军，俞永强，等.地球系统模式发展展望[J].气象学报，2008，66(6)：857-869.

[2] HUANG M，HOU Z，LEUNG L R，et al.Uncertainty analysis of runoff simulations and parameter identifiability in the community land model：evidence from MOPEX basins[J].Journal of Hydrometeorology，2013，14(6)：1754-1772.

[3] GILMORE M S，STRAKA J M，RASMUSSEN E N.Precipitation uncertainty due to variations in precipitation particle parameters within a simple microphysics scheme[J].Monthly Weather Review，2004，132(11)：2610-2627.

[4] SALTELLI A，RATTO M，TARANTOLA S，et al.Sensitivity analysis for chemical models[J].Chemical Reviews，2005，105(7)：2811-2828.

[5] SONG X，ZHANG J，ZHAN C，et al.Global sensitivity analysis in hydrological modeling：review of concepts，methods，theoretical framework，and applications[J].Journal of Hydrology，2015，523：739-757.

[6] LI J，DUAN Q Y，GONG W，et al.Assessing parameter importance of the common land model based on qualitative and quantitative sensitivity analysis[J].Hydrology and Earth System Sciences，2013，17(8)：3279.

[7] METZGER C，NILSSON M B，PEICHL M，et al.Parameter interactions and sensitivity analysis for modelling carbon heat and water fluxes in a natural peatland, using Coup-Model v5[J].Geoscientific Model Development，2016，9(12)：4313-4338.

[8] GAN Y，DUAN Q，GONG W，et al.A comprehensive evaluation of various sensitivity analysis methods：a case study with a hydrological model[J].Environmental Modelling and Software，2014，51：269-285.

[9] SAFTA C，RICCIUTO D，SARGSYAN K，et al.Global sensitivity analysis，probabilistic calibration，and predictive assessment for the data assimilation linked ecosystem carbon model[J].Geoscientific Model Development Discussions，2015，8(7):6893-6948.

[10] MOON H.Design and analysis of computer experiments for screening input variables[D].Columbus, Ohio: The Ohio State University，2010.

[11] U K M，ARAKAWA A.Semiprognostic tests of the Arakawa-Schubert cumulus parameterization using simulated data[J].Journal of the atmospheric sciences，1992，49(24)：2421-2436.

[12] ZHANG M H，LIN J L.Constrained variational analysis of sounding data based on column-integrated budgets of mass，heat，moisture，and momentum：approach and application to ARM measurements[J].Journal of the Atmospheric Sciences，1997，54(11)：1503-1524.

资助项目：国家重点研发计划项目（2016YFA0602103）

作者信息:

黄  欣1，李倩玉2，骆亦其3，薛  巍1，2

（1.清华大学 计算机科学与技术系，北京100084；2.清华大学 地球系统科学系，北京100084；

3.北亚利桑那大学 生态系统科学与社会中心，美国 弗拉格斯塔夫 86011）