0 引言

    随着科学技术的不断发展，大量的非线性负载和电力电子设备被应用在工业生产和日常生活中，这提高了生产效率，促进了生活便利，但同时也对电网造成了巨大的谐波污染。另一方面，随着新能源在电力系统中的迅速发展，各种分布式的电源也相继产生，比如太阳能发电、风力发电以及地热能等，这些新能源的发电设备并网运行时，同样也给电力系统带来了一系列谐波污染，因此谐波污染治理也越发重要^[1]。谐波污染治理的性能很大程度上又受到谐波检测环节的影响，这就要求谐波检测过程必须要具备两个特点：实时性强、准确度高^[2]。电力系统中常用的谐波检测的方法主要有傅里叶变换^[3]、小波变换^[4]和希尔伯特-黄变换^[5]等。在治理谐波污染时性能表现不佳，分别体现在易产生频谱泄漏和栅栏效应、算法计算量过大和不具有自适应性以及容易产生模态混叠效应和负频率。

    近年来，Prony算法因其具有高频率分辨率和高频率估计精度，在电力系统中获得了越来越多的关注。但是，Prony算法对于噪声较为敏感，易受噪声信号的影响。电网系统中包含着大量的高斯噪声，因此如何能够降低噪声对模型辨识的影响成为了一个难点。文献[6]提出了Prony算法与小波分析相结合的方法，先通过小波函数对扰动信号进行分解，然后利用改进的Prony算法对稳态扰动问题进行参数辨识，虽然提高了辨识精度，但是该算法过于依赖对小波基的选择，滤波效果并不理想。文献[7]提出了将SVD滤波技术与Prony算法相结合的方法，该方法利用SVD的特性滤除噪声信号，其次利用Prony算法对信号进行处理，但是SVD滤波处理过程中太过依赖奇异值有效阶次的判断，同样不具备自适应性。

    本文在前人研究的基础上，提出了一种基于SVD的改进滤波算法，能够精确地找到电网信号中谐波及间谐波信号分量的阶次，同时滤除电网信号中的噪声信号，只留下“纯净的”电网信号。根据滤波后的电网信号以及谐波及间谐波信号阶数，利用一种改进的Prony算法，结合线性神经网络，计算出信号的频率、相位和幅值。研究结果表明，算法对于谐波信号的检测精确度极高，同时由于所需的采样数据长度小，实时性也较强，能够很好地满足实时性和准确度的要求。

1 电网信号模型

    电网信号主要包含基波各次谐波、间谐波以及各种噪声信号，因此可以通过以下数学表达式来建立模型：

式中，w_i=2πf_i，p为谐波和间谐波个数，A_i、f_i、θ_i分别表示第i个谐波或间谐波信号的幅值、频率和相位，而ω(n)则表示电网系统中的噪声信号。

    根据电网的特性，除了基波分量以外，奇次谐波分量对电网的影响所占权重较大，本文主要选取了奇次谐波中影响较大的3次、5次以及7次谐波作为电网信号的模型^[8]；间谐波主要存在于谐波附近，易受谐波信号影响。因此，本文基于谐波信号选择了3个间谐波信号。谐波检测算法的作用是对式(1)的正弦信号进行参数辨识，得到各个谐波和间谐波信号的特性参数，本文所提算法正是基于此电网信号模型。

2 算法实现

2.1 基于SVD的改进滤波算法

    电网信号模型为x(i)=s(i)+w(i)(i=1，2，…，N)。将接收到的电能信号序列x=[x₁，x₂，…，x_N]构造成如下的Hankel矩阵的形式：

其中，当N为偶数时，n=N/2，m=N/2+1；当N为奇数时n=(N+1)/2，m=(n+1)/2。

完成对信号序列的Hankel矩阵X的构造以后，对X进行奇异值分解，可得到：

    信号的完备空间可以划分为信号子空间和噪声子空间，并且它们之间相互正交。在奇异值分解理论中，奇异值的前k个值对应着信号子空间分量，后q-k个奇异值则对应着噪声子空间分量。因此，称k为信号的有效阶次。

    信号分解的奇异值序列的分布具有其特点：在有效阶次k之前，奇异值内部差异都相对较小，变化也比较平缓；而在第k+1个奇异值处，奇异值序列出现明显的阶跃式下降；之后奇异值序列的变化再次趋于平缓，不存在明显波动^[9]。如果将获得的奇异值序列看作一个信号序列，根据奇异值序列的这种特性寻找到相应的突变点作为奇异点，那么这个突变点的位置就是原信号中有效阶次。

    对于电网信号来说，在确定有效阶次为k后，如果k的值过小，虽然大部分噪声信号都被滤除，但是大量的电能信号也已丢失；如果k的值过大，电能信号虽保持完整，但是噪声信号未能得到很好的滤除，干扰仍较大。因此，如何更好地确定有效阶次对于滤波的效果至关重要。本文在结合对电网信号的特性分析以及奇异值分解理论后，提出一种奇异点辅助算法，根据奇异值增长率的变化，确定奇异值突变点，辅助确定奇异值的有效阶次。奇异值增长率公式为：

式中，σ_i为第i个奇异值，η_i为第i+1个奇异值同比上一个奇异值的下降率。通过对η_i大小的比较，选择η_i最大的i处作为奇异点位置。

    对矩阵X进行奇异值分解之后，利用式(6)对信号进行重构：

2.2 改进的Prony-ADALINE算法

    Prony算法是一种使用指数函数的线性组合来描述等间距采样数据的理论，可以用来估计有理式功率谱密度^[10]。传统的算法采用的数学模型为p个具有任意幅值、相位、频率与衰减因子的指数函数，本文的信号为正弦信号，因此，采样Prony谱线估计算法^[11]，其数学模型为p个实的、无衰减的正弦信号。

2.2.1 Prony谱线估计算法

    Prony谱线估计算法的数学模型用离散时间的函数表示为：

    本文改进的算法主要包括以下步骤：

    (1)定义样本函数(10)，根据滤波处理后的信号以及得到的信号的有效阶次k(即特征多项式中2p=k)，利用样本函数构建样本矩阵，并通过样本矩阵构建法方程(11)：

2.2.2 ADALINE神经网络算法

    ADALINE神经网络是一种结构较为简单的神经网络模型，现在已经广泛应用于自适应信号处理领域，对于电网信号中的谐波和间谐波信号分析也同样适用。ADALINE神经网络算法和其他神经网络相比，它的最大优势就是不需要事先对神经网络进行大量训练，同时它还具有分析精度高、收敛速度快这一突出特点，因此可以做到对电网信号中的谐波和间谐波信号成分的实时分析。

    根据三角函数的特点，对式(8)进行三角恒等变换，得到式(13)：

    基于ADALINE模型的检测原理图如图1所示，分为输入层、求和层和输出层。其中输入信号X(n)= [ cos(2πf₁n)，sin(2πf₁n)，…，cos(2πf_pn)，sin(2πf_pn)]，输入神经元数即等于有效阶次2p。对应的权系数为W(n)=[a₁，b₁，…，a_p，b_p]^T。输入信号与权系数相乘，经过求和层，得到单个的输出向量y(n)。权值更新算法自动更新权系数W(n)，使之不断收敛到稳态阶段，这时的权系数即为逼近式(13)中的系数，实现谐波及间谐波的幅值、相位检测。

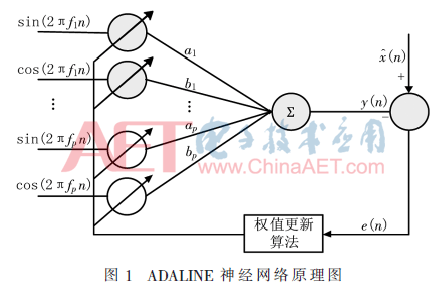
    该神经网络结构的基本特点可总结为如下三个方面：

    (1)可以根据变化着的输入和目标输出实现实时在线训练；

    (2)应用自适应在线算法调整各权值大小；

    (3)结构简单，便于硬件实现。

3 仿真分析

    实际电网中，电网信号相对比较复杂，包含了众多的谐波、间谐波以及噪声信号等。本节主要对电网电压信号进行仿真并分析，建立的信号模型的表达式如式(14)所示，通过利用MATLAB软件对信号进行仿真分析，用以分析和验证本文所提算法应用在谐波检测的性能。

式中，ω(t)为加在谐波信号上的噪声，信噪比为30 dB，各个谐波以及间谐波的具体参数如表1所示。本次信号采样点个数为400，采样频率为1 500 Hz，采样时间为0.27 s。

3.1 滤波算法性能分析

    对于采样的电网信号，根据式(2)构造Hankel矩阵X，对其进行奇异值分解，得到奇异值序列σ。根据本文提出的奇异值辅助算法，通过对奇异值序列的运算，得到如图2所示的奇异值增长率曲线。

    图2中横坐标表示的为奇异值序列，纵坐标为根据辅助算法计算出的奇异值增长率。由图2可知，奇异值增长率在横坐标为0～14区间变化较大；在超过14后，增长率降低，接近于0，变化趋于稳定。这是因为各次谐波分量的能量差距较大导致。增长率在奇异值序列为2时达到80%以上，是由于基频信号与其他谐波成分能量相差过大。当奇异值序列取值为14时，此时的增长率接近于1，达到最大值。对比数据可知，该处即为有效阶次，通过该辅助算法确定的有效阶次与实际的完全一致。

    根据已经得到的奇异值的有效阶次，对信号进行SVD滤波处理，滤波结果如图3所示。图3中分别是未加噪声的原始谐波信号、加噪声的谐波信号以及SVD滤波后的谐波信号的局部波形图。

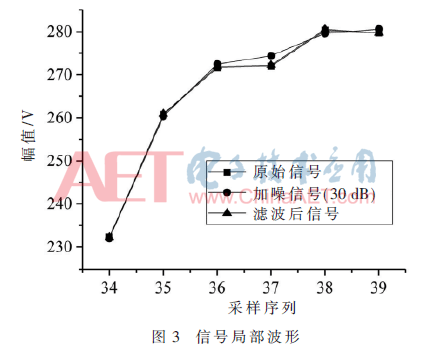
    从图3中原始信号、包含噪声信号以及滤波后信号的对比可看出，滤波后的信号波形几乎与原始信号完全重合。这是因为本文提出的算法能够准确地确定信号的有效阶次，进而能够有效滤除噪声成分，降低噪声对谐波检测算法影响的同时，又没有损失信号中的有效成分，为Prony谱线估计算法提供了一个“纯净”的电能信号。

3.2 谐波检测算法性能分析

    为了验证本文方法的有效性，通过采样本文所提算法与文献[12]中的数学形态学+改进Prony算法进行对比，其中，算法1为本文算法，算法2为文献中所提算法。两种算法对于信号特性参数中频率的估计结果如表2所示，对于幅值和相位特性参数的估计则通过图4以相对误差的形式给出。

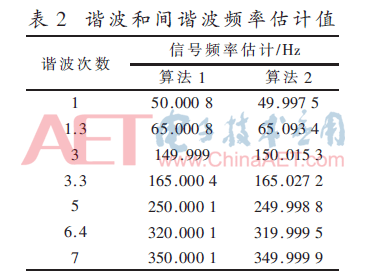
    表2是两种算法对于电网信号对频率估计的计算数值结果，两种算法对于谐波分量的频率估计误差已经很小，接近实际频率值，估计精确度极高。其中在对于间谐波分量的频率进行计算时发现，算法2在对于1.3次间谐波的频率进行计算时，计算值与实际参数值相差0.093 4 Hz，而算法1的计算值与实际参数值误差则仅为0.000 8 Hz，在3.3次间谐波分量处算法2的计算误差同样远大于算法1，而在6.4次间谐波处两种算法的计算误差逐渐降低，趋于平缓。

    图4表示的是两种算法对于幅值和相位这两个参数计算数值的相对误差。由图可知，算法1对于幅值的计算在1.3以及3.3次谐波处的相对误差远小于算法2的相对误差，且计算结果满足文献[13]中规定的A类测量仪器要求的相对误差小于5%。在对于相位计算过程中，算法1计算的相对误差最高也仅为1.5%，检测精确度比算法2更高。

4 结论

    本文针对Prony算法对噪声信号敏感的问题，提出了一种基于SVD改进算法。采用了自适应的辅助算法帮助奇异值序列找到有效阶次，替代了传统的奇异值曲线以及奇异熵增量等经验性的方法，更好地滤除噪声信号。同时，基于有效阶次，将SVD更好地与Prony算法结合在一起，使用简单的线性方程组的求解去替代最小二乘法，降低了算法运算量。在此基础上进行仿真验证，仿真结果表明该方法准确、有效，具有一定的工程应用价值。

参考文献

[1] BAGHERI A，MARDANEH M，RAJAEI A，et al.Detection of grid voltage fundamental and harmonic components using Kalman filter and generalized averaging method[J].IEEE Transactions on Power Electronics，2015，31(2)：1064-1073.

[2] 彭咏龙，张坤锋，李亚斌，等.基于自适应算法的谐波检测方法研究[J].电测与仪表，2018，55(9)：6-9.

[3] Su Taixin，Yang Mingfa，Jin Tao，et al.Power harmonic and interharmonic detection method in renewable power based on Nuttall double-window all-phase FFT algorithm[J].IET Renewable Power Generation，2018，12(8)：953-961.

[4] TSE N C F，CHAN J Y C，LAU W H，et al.Hybrid wavelet and hilbert transform with frequency-shifting decomposition for power quality analysis[J].IEEE Transactions on Instrumentation and Measurement，2012，61(12)：3225-3233.

[5] 李正明，徐敏，潘天红，等.基于小波变换和HHT的分布式并网系统谐波检测方法[J].电力系统保护与控制，2014，42(4)：34-39.

[6] 任子晖，刘昊岳，徐进霞.基于小波变换和改进Prony方法的电能质量扰动分析[J].电力系统保护与控制，2016，44(9)：122-128.

[7] 许伯强，田士华.SVD滤波技术与Prony谱线估计算法相结合的异步电动机转子故障检测新方法[J].电机与控制应用，2015，42(10)：41-47.

[8] 刘冬梅，杨重良，张艳，等.基于Nuttall自卷积窗四谱线插值FFT的电力谐波分析方法[J].合肥工业大学学报，2018，41(3)：12-17.

[9] 查翔，倪世宏，谢川，等.奇异值分解去噪中有效秩阶次的自身辅助确定[J].计算机应用研究，2016，33(5)：1359-1362.

[10] 熊杰锋.基于加窗插值和Prony的电力系统间谐波算法[J].电力系统保护与控制，2011，39(7)：8-13，19.

[11] 张贤达.现代信号处理[M].北京：清华大学出版社，2002.

[12] 公茂法，蔡芬，刘俊杰，等.基于数学形态学和改进Prony算法的谐波与间谐波参数估计[J].电测与仪表，2018，55(11)：25-29，40.

[13] GB/T 24337-2009，电能质量 公用电网间谐波[S].2009.

作者信息:

应  俊1，2，朱云鹏1，2，贺  超2

(1.重庆邮电大学 光电工程学院，重庆400065；2.重庆邮电大学 光通信与网络重点实验室，重庆400065)