0 引言

    矿山排土场滑坡是一种非常普遍发生的地质灾害，由于滑坡的频繁发生，每年都会造成大量的人员伤亡和巨额的财产损失。很多排土场都存在着滑坡风险，排土场的堆放位置以及堆放方式和管理方式的不合适可能会造成滑坡事故的发生。随着传感器技术的发展，各种类型的传感器相继被应用到了矿山排土场的安全监测当中，传感器能长时间保持不间断地采集排土场的相关指标，这些相关指标对排土场的安全指标具有重大意义，在一定程度上体现着排土场的稳定状态。传感器传输的实时数据代表排土场的某一时刻相关特征指标的值，但是当技术人员接收到异常数据时，排土场滑坡或许已经发生了，若能够提前预测出传感器下一时刻的信息，可以有效降低排土场滑坡造成的财产损失和人员伤亡，到目前为止，矿山排土场滑坡灾害预警仍然是一个处于探索阶段的世界性难题^[1]。

    目前关于滑坡预测方法主要是分析滑坡位移随时间变化的曲线及各类直接或间接影响滑坡产生的环境影响因子的监测信息^[2]，来反演滑坡内在的非线性动力学变化过程，进而建立起滑坡位移同各个环境影响因子之间的非线性映射关系，最终达到预测滑坡位移的变化趋势的效果。传统的滑坡预测模型主要以时间序列分析方法和各类统计方法预测为主^[3]，这些方法在智能性、精确性和及时性方面都存在着较大的缺陷。为了有效提高对滑坡的预测能力，本文提出了一种AdaBoost的粒子群优化极限学习机的集成学习方法实现滑坡位移预测（AdaBoost-PSO-ELM），与以往方法相比，其具有以下优点：(1)利用粒子群优化算法（Particle Swarm Optimization，PSO）来优化极限学习机（Extreme Learning Machine，ELM）的输出权重和隐层偏置，解决了人工参数整定困难的问题^[4]，提高了预测效率；(2)采用多神经网络集成学习算法，提高网络预测泛化能力；(3)引入AdaBoost算法极大降低了ELM陷入局部最优的风险，进一步提高了预测精度。

1 算法分析与设计

1.1 极限学习机模型

    极限学习机(Extreme Learning Machine，ELM)是HUANG G B等在2006年提出的一种单隐含层前馈神经网络（Single Hidden Layer Feedforward Neural Networks，SLFNN）的算法，该算法随机产生输入层与隐含层的连接权值及隐含层神经元的偏置^[5]，构建无需任何迭代的单隐层神经网络，与传统神经网络相比，通过一步计算即可解析出网络的输出权值，大大提高了网络的泛化能力和学习速度，具有较强的非线性拟合能力。ELM的网络结构如图1所示。

1.2 粒子群优化算法

    粒子群优化算法(Particle Swarm Optimization，PSO)的基本思想源于鸟群的觅食行为，每个粒子在初始阶段都会被初始化为一定的速度、位置和一个由适应度函数决定的适应值，同时每个粒子都被赋予记忆功能。在每一次迭代寻优的过程中，粒子通过比较适应度值和两个边界值来更新自己的速度和位置，通过不断的更新速度和位置，粒子本身最终能找到个体最优解和整个种群全局最优解^[6]。

    利用动态惯性权重ω的方法提高粒子群的寻优能力进而加快极限学习机（ELM）的预测效率和提高预测精度，较高的惯性权重ω会使粒子群算法有更好的全局的寻优能力，而较低的惯性权重ω则对于局部寻优效果更好^[7]，粒子速度和位置更新表述如下：

    本文中以实际值与预测值的均方误差（MSE）作为粒子寻优的适应度函数^[8]：

    利用PSO寻找ELM中最优的隐含层节点数、输入权值和隐含层偏置，使获得的模型更能准确预测滑坡的地表位移。

1.3 AdaBoost的粒子群优化极限学习机算法（AdaBoost-PSO-ELM）设计

    AdaBoost算法是Boosting思想的机器学习算法，其核心思想先从初始训练集训练出一个基学习器，根据基学习器的表现对训练样本进行调整，使得先前基学习器做错的训练样本在后续受到更多的关注，然后基于调整后的样本分布来训练下一个基学习器，重复进行，直至基学习器数目达到指定的值^[9]。

    本文提出的AdaBoost-PSO-ELM算法基本思想是：初始化一个ELM基学习器，反复训练得到多个ELM的弱预测器，使用AdaBoost算法将得到的多个ELM弱预测器组成一个强预测器，进一步提高ELM网络的预测准确率，降低ELM网络陷入局部最优的风险^[10]，提高ELM的泛化能力。AdaBoost-PSO-ELM算法流程如图2所示。其详细步骤如下：

    (1)给定输入样本。对ELM网络、PSO相关参数进行初始化，从输入样本数据中选取训练集中的m组数据，初始化测试数据分布权值D₁=(1/g，…，1/g)_1×m，根据输入输出样本的特性指标维度确定ELM网络结构。

    (2)输入样本数据预处理。其中包括异常值处理、空缺值填补、无量纲化等，对异常值作为缺失值处理，通过拉格朗日插值法对所有空缺值进行插值填补；排土场数据集中每个特性指标间的单位存在量纲差异，为消除不同量纲间对预测精度的影响，对排土场数据进行无量纲化处理^[11]；

    (3)通过PSO优化ELM的输入参数，同时得到多个ELM弱预测器，在训练第n个ELM弱预测器时，使用ELM对训练集数据进行训练，得到预测序列的预测误差和error_n，误差和error_n的公式如式(10)所示：

2 试验研究与结果分析

    为验证本文提出的AdaBoost的粒子群优化极限学习机算法的有效性和准确性，采用中国贵州某矿山排土场在2016年12月～2017年11月间从传感器中采集到的该矿山排土场的各特性指标数据，各指标数据每隔半小时到一小时更新一次，总共含有14 423条数据，其中被选取的特性指标有地表位移（Mp）、土压力（Dm）、土壤含水率（Smc）、降雨量（Rg）、孔隙水压力（St）、湿度（Hum）、温度（Tpr）、内部位移（Ep）共8个指标。

    8个指标中，地表位移是最直观、最能反映排土场边坡变化趋势的观测性指标；边坡内部位移最能反映滑坡体多层变形和滑带的位置，是滑坡监测的一个非常重要的监测对象；同时降雨量、土壤含水率、土压力、孔隙水压力、湿度和温度也会直接或间接地影响到前面指标的变化。本文将地表位移作为判断排土场滑坡的直接因素，其余特性指标作为间接判断排土场滑坡的综合因素。本文主要进行了3个模型的验证分析，将数据集的前70%作为训练数据，后30%作为验证数据，以均方根误差（RMSE）作为性能评价指标。

    本文做了3组对比试验,分别为ELM、PSO-ELM、AdaBoost-PSO-ELM模型对地表位移的预测，其他7个特性指标作为目标的输入。首先，采用ELM进行地表位移的预测，图3所示的是ELM对地表位移的预测效果曲线图，该模型随机初始化一组输入权值和隐含层偏置，采用sigmoid函数作为激活函数，神经元的个数为100，从图中可以看出，预测效果不是很好，RMSE的值为2.89。

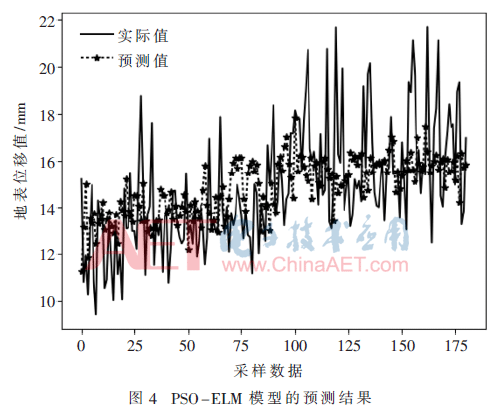
    为避免ELM输入参数随机化，利用PSO得到ELM的输入权值和隐含层偏置，种群为100的粒子群，其预测效果如图4所示，预测效果比ELM网络有了一定的提高，同时也基本拟合了真实曲线的趋势，其RMSE的值为2.62，但是在精度方面还有上升的空间。图5表示的是PSO在寻优过程中的迭代次数和均方误差的关系，从图中可以看出在迭代的初期，粒子群的收敛速度很快，变化率很大，随着迭代次数的增加，粒子群的收敛速度趋于平缓，PSO在寻优过程中迭代到100次左右已开始收敛。

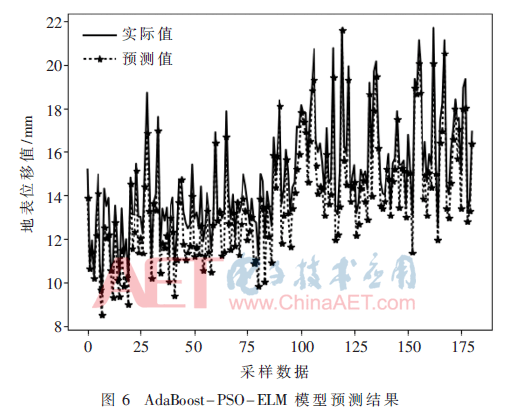
    PSO寻优过程无法完全避免种群陷入局部最优风险，本文提出在PSO优化ELM的基础上，采用AdaBoost算法进一步提升ELM预测的准确性，构造10个由ELM组成的弱预测器，利用AdaBoost算法将10个ELM弱预测器构成一个强预测器。实验结果表明，该方法可以大幅度提升ELM预测精度，如图6所示，从图中可以发现经AdaBoost的粒子群优化的预测值与真实值的曲线趋势基本处于同步，真实值与预测值曲线的间隔比起前两种模型处理的效果有明显的提高，预测结果能很好地拟合真实值，其RMSE的值为1.17。3组对比实验的RMSE如表1所示。

3 结论

    矿山排土场滑坡的过程是一个动态、大延迟、高度非线性的特性问题，影响矿山排土场滑坡的因素众多，同时PSO无法避免陷入局部最优风险。对此，本文提出AdaBoost-PSO-ELM算法构成的强预测器方法，利用PSO算法确定了ELM的输入权值，提高了ELM的学习效率，解决了人工参数整定难的问题。本文的具体思路是将ELM作为基学习器，经过反复训练ELM的预测输出，得到由多个ELM的弱预测器组成的强预测器。实验结果表明，该方法具有较高的预测精度，有效地提高了矿山排土场滑坡位移预测精度。

参考文献

[1] 秦宏楠.紫金山金铜矿排土场滑坡诱发机理及监测预警技术研究[D].北京：北京科技大学，2016.

[2] 张艳博，张国锋，田宝柱，等.露天煤矿边坡稳态影响因子敏感性分析及滑坡控制对策[J].煤炭工程，2011，1(5):105-107.

[3] 徐峰，汪洋，杜娟，等.基于时间序列分析的滑坡位移预测模型研究[J].岩石力学与工程学报，2011，30(4)：746-751.

[4] 杨向萍，吴玉丹.基于PSO-BP神经网络的人体穴位定位系统设计[J].电子技术应用，2018，44(9）：75-78.

[5] HUANG G B，WANG D H，LAN Y.Extreme learning machines：a survey[J].International Journal of Machine Learning & Cybernetics，2011，2(2)：107-122.

[6] 杨锡运，关文渊，刘玉奇，等.基于粒子群优化的核极限学习机模型的风电功率区间预测方法[J].中国电机工程学报，2015，35(S1)：146-153.

[7] 李艳，杨华芬.一种改进的动态惯性权重粒子群优化算法[J].长春工程学院学报(自然科学版)，2014(4)：116-119.

[8] ABREU L D，ROMERO J L.MSE estimates for multitaper spectral estimation and off-grid compressive sensing[J].IEEE Transactions on Information Theory，2017，PP(99)：1.

[9] GUO H，LI Y，LI Y，et al.BPSO-Adaboost-KNN ensemble learning algorithm for multi-class imbalanced data classification[J].Engineering Applications of Artificial Intelligence，2016，49(C)：176-193.

[10] 赵英刚，龚垒.基于行为识别和SVM的短信过滤方法研究[J].微计算机信息，2012(1)：176-177.

[11] 曹国清，张晓明，陈亚峰.基于PCA-LSTM的多变量矿山排土场滑坡预警研究[J].计算机系统应用，2018，27(11)：252-258.

作者信息:

张晓明1，曹国清1，2，陈增强1，何佳康1，2

(1.北京石油化工学院 信息工程学院，北京102617；2.北京化工大学 信息科学与技术学院，北京100029)