0 引言

    物体建模往往需要大量人力和物力，但随着计算机算力提高，计算机视觉研究的不断深入和摄影设备的普及，基于视觉的建模技术成为解决此问题的一种新方法，并成功运用于文物保护、增强现实、自动驾驶、大规模场景三维重建以及医学图像处理等领域^[1]。三维重建作为计算机视觉的一个重要研究内容，基于Marr理论框架，形成了多种理论方法，运动恢复结构(Structure from Motion，SFM)方法^[2]是最广泛采用的方法之一。近年来，基于SFM研制出多种建模系统，如Visual SFM^[3]、ETH-3D^[4]、LS-ACTS^[5]等。

    特征点匹配是基于SFM重建算法中最关键的一步，直接影响重建效果^[2]。目前主要匹配算法有KLT(Kanade Lucas Tomasi Tracking，KLT)算法^[6]、尺度不变特征转换(Scale Invariant Feature Transform，SIFT)算法^[7]和加速稳健特征(Speeded Up Robust Features，SURF)算法^[8]等，以及一些上述算法的改进算法，如基于仿射变换的SURF算法^[9]。文献[10]采用SIFT算法提取图像特征点并匹配，结合相机参数将一组匹配点映射为一组空间直线，由于各种误差的存在，直线间将异面，取异面直线公垂线的中点为三维空间点。但SIFT算法实时性差，不利于未来工程应用。文献[11]使用SURF算法，寻找图像序列中的特征点，利用随机抽样一致(Random Sample Consensus，RANSAC)算法优化求解相机位置参数，得到图像的投影矩阵，并三角化生成空间点云，利用投影矩阵将三维点反投影回原图像，消除与原匹配点误差太大的特征点。但SIFT和SURF算法得到的匹配数据都比较稀疏，导致模型不完整。

    基础矩阵描述了两幅图像间对极几何的关系，估计基础矩阵是重建过程中重要的一步。估计基础矩阵常用的方法有七点法和八点法等方法，具有计算速度快的优点，但对噪声敏感^[12]。HARLEY R I提出了归一化八点算法，在估计基础矩阵前对匹配点归一化处理，提高了算法的抗噪能力^[13]。

    在基于SFM重建算法中，基础矩阵的估计要求匹配数据精度高，三角化重建要求匹配数据数量大，二者对匹配数据的要求不同。本文提出一种采用不同匹配数据的重建算法，首先通过对比上下文直方图(Contrast context histogram，CCH)算法^[14-15]提取图像匹配点对，使用归一化八点算法和M估计抽样一致(M-estimator Sample and Consensus，MSAC)算法^[11]计算基础矩阵F，结合摄像机内参得到本质矩阵后，计算图像旋转矩阵R和平移矩阵T，并得到相机投影矩阵P；然后使用KLT特征跟踪算法更新匹配数据，三角化得到匹配点三维信息；最后将图像匹配点的颜色赋予三维空间点，得到具有颜色信息的点云模型。实验表明，本文算法能有效得到目标点云模型。

1 相关研究工作

1.1 CCH匹配算法

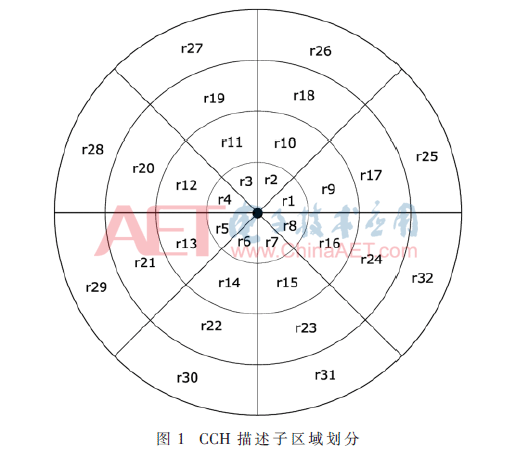
    计算CCH描述子之前，通过多尺度拉普拉斯金字塔下提取Harris角点^[15]。将每一个角点P_c的邻域分为4个同心圆，每个圆区域均匀分为8个不重叠子区域，因此，存在32个子区域(r₁，r₂，…，r₃₂)。将P_c点的方向设置为CCH描述子的0°方向，并以最小半径同心圆0°的子区域为r₁，如图1所示。定义角点P_c邻域内一点P的对比度值：

    遍历待匹配图像和匹配图像之间的特征点以进行匹配，CCH算法采用基于最近距离的匹配：

1.2 KLT算法

    SFM建模算法为获得高质量的匹配数据，使用的图像大都是在尺度和光照等条件相差不大时取得的，而这正满足KLT算法的假设。Kanade等提出的KLT算法假设在图像的亮度恒定或相差不大、空间一致或有小运动情况下，通过计算特征点的位移，得到对应的匹配点^[6]。

    KLT算法采用计算Hessian矩阵特征值的方法提取图像上特征点。假定在t时刻图像中的一点P₁(x，y)，对应灰度为I(x，y，t)，经过时间dt后运动到新的位置P₂(x+dx，y+dy)，对应的灰度为I(x+dx，y+dy，t+dt)，d=[dx，dy]为位移量，dt为时间变化量。

式中，I_r为两帧图像局部窗口内灰度之差，因而位移d=G^-1e，从而得到该点对应的匹配点。

2 改进的三维重建算法

2.1 基础矩阵估算

2.2 投影矩阵计算

    从二维图像得到三维空间信息，需要相机的参数，包括相机内参矩阵K、平移矩阵T和旋转矩阵R。

其中，[R  t]为3×4的外参矩阵，P=K×[R  t]为内外参组合后3×4的投影矩阵。

2.3 三角化

2.4 改进三维重建的流程

    序列图像的重建是在两幅图像重建基础上通过增加匹配数据，得到更密集的点云。所以两幅图像的重建是SFM重建的基础，若两幅图像间重建得到大量的数据，可以极大地减少工作量。本文均以两幅图像为重建数据，分为以下几步：

    (1)计算CCH描述子：导入图像，根据1.1节中方法得到CCH描述子，并得到匹配点对；

    (2)估计基础矩阵F：基础矩阵的估计是为了得到本质矩阵E。使用2.1节中提到的方法估计基础矩阵，结合内参矩阵得到本质矩阵；

    (3)计算投影矩阵P：通过对本质矩阵E的分解得旋转矩阵R和平移矩阵T，结合相机内参恢复出相机的投影矩阵；

    (4)更新匹配数据：采用1.2节中提到的KLT算法，跟踪特征点，更新匹配数据；

    (5)三角化：利用2.3节方法，计算三维点生成点云；

    (6)点着色：将图像匹配点对的颜色赋予空间三维点，得到有色彩的点云。

3 实验结果与分析

    本文算法在Intel i3 CPU、4 GB RAM的Windows 7操作系统下，使用MATLAB R2016a实现。实验由两部分组成：(1)Fountain和Herz-Jesu图像^[16]，并将本文算法与文献[10]和文献[11]中的算法进行对比；(2)Desktop和Symbol图像，采用IMX258摄像头(Nubia手机内置)拍摄，分别为电脑桌面和西南科技大学制造科学与工程学院标志，以验证本文算法在真实场景下的可行性。

3.1 算法对比实验

    图2和图3分别为Fountain图像和Herz-Jesu图像重建结果，算法均采用为两幅图像重建生成点云，图中只列举了其中一幅，表1和表2为重建点云的数量和时间的对比。可以看到本文算法生成的点云在点的数量上优势明显。Herz-Jesu图像分辨率为3 024×2 048，建模效果比分辨率为720×480的Fountain图像要好，因为高分辨率意味着更丰富的信息。采用文献[10]和文献[11]中特征提取与匹配的方法，在特征匹配阶段，对于图像低频特征区域，描述子之间相似度较高，容易被认为是误匹配而被剔除，导致显示为空洞，如Herz-Jesu图像的“墙”部分，而采用本文算法可以得到“墙”部分点云。

    基于SIFT和SURF提取特征并匹配的方法，能够在图像光照、旋转及尺度等多种条件的变化下取得很好的匹配效果。而对于SFM来说，图像都是在光照和尺度等条件变化比较小的情况下取得的，以相机为参考系，可以认为场景内物体进行了小运动。此前提下，采用KLT特征追踪算法更新匹配数据，可以得到更好的效果。KLT算法基于特征的小运动假说，通过计算特征点的位移实现匹配，在图像低频区域，避免了特征点匹配时描述子相似度高而被剔除。因此，对于SFM重建方法，生成点云时，使用基于KLT的跟踪算法更合适。

    SFM三维重建方法中两次使用匹配数据，第一次用于计算基础矩阵，第二次用于三维重建。在图像匹配上CCH算法具有很高精度，同时匹配点数量较其他方法减少，利于MSAC算法迭代计算基础矩阵，使计算结果收敛。

3.2 真实场景重建实验

    采用张正友相机标定方法将IMX258摄像头进行相机标定，标定得到对应于式(10)中相机的参数：α_x=3 115.833 678、γ=7.867 908、u₀=1 527.096 651、α_y=3 132.207 642、v₀=2 073.525 058。表3为使用本文算法得到的图像运动参数。图4(a)和图4(c)为拍摄得到的Desktop图像与Symbol图像，分辨率均为4 160×3 120；图4(b)和图4(d)分别是使用本文算法建模的对应结果，点云模型点数量分别为43 374和56 013。可以看出，采用本文算法实现的物体的三维重建，其得到的点云模型相对完整。

4 结束语

    本文通过分析基于SFM的三维重建算法对匹配数据的要求不同，提出一种改进的三维重建算法。使用CCH算法得到匹配数据计算基础矩阵，使用KLT角点跟踪算法更新匹配数据，最后得到有色彩的点云模型。与现有的算法相比，本文算法在图像低频区域能得到更丰富的匹配数据，重建模型更完整。

    本文算法实现了基于图像的建模，并取得了较好效果。由于手机透镜采用塑胶透镜，光学性能较玻璃透镜低；同时手机CMOS传感器性能比专业单反低。因此Desktop和Symbol的图像质量比Fountain和Herz-Jesu差，下一步将研究提高手机拍摄图像质量的算法，结合本文算法开发基于序列图像的三维重建APP，实现使用手机完成图像的拍摄和重建全过程。

参考文献

[1] 佟帅，徐晓刚，易成涛，等.基于视觉的三维重建技术综述[J].计算机应用研究，2011，28(7)：2411-2417.

[2] CAO M，CAO L，JIA W，et al.Evaluation of local features for structure from motion[J].Multimedia Tools & Applications，2018，77(9)：1-15.

[3] WU C.Towards linear-time incremental structure from motion[C].International Conference on 3D Vision，IEEE Computer Society，2013：127-134.

[4] ZACH C.Robust bundle adjustment revisited[C].European Conference on Computer Vision.Springer，2014：772-787.

[5] ZHANG G，LIU H，DONG Z，et al.Efficient non-consecutive feature tracking for robust structure from motion[J].IEEE Trans Image Process，2015，25(12)：5957-5970.

[6] SHI J，TOMASI C.Good features to track[C].Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.IEEE，2002：593-600.

[7] LOWE D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision，2004，60(2)：91-110.

[8] BAY H，ESS A，TUYTELAARS T，et al.Speeded-up robust features[J].Computer Vision & Image Understanding，2008，110(3)：404-417.

[9] 刘欣，李校林，谢灿，等.一种基于仿射变换的SURF图像配准算法[J].电子技术应用，2014，40(6)：130-132.

[10] 胡影峰.基于SIFT特征匹配算子的三维重建方法研究[J].自动化仪表，2011，32(1)：30-32.

[11] 景子君.运动法三维重建的研究与实现[D].合肥：中国科学技术大学，2018.

[12] 阚江明.基于计算机视觉的活立木三维重建方法[D].北京：北京林业大学，2008.

[13] HARTLEY R I.In defence of the 8-point algorithm[C].International Conference on Computer Vision，IEEE Computer Society，1995：1064-1070.

[14] HUANG C R，CHEN C S，CHUNG P C.Contrast context histogram a discriminating local descriptor for image matching[C].International Conference on Pattern Recognition.IEEE，2006：53-56.

[15] HUANG C R，CHEN C S，CHUNG P C.Contrast context histogram—An efficient discriminating local descriptor for object recognition and image matching[J].Pattern Recognition，2008，41(10)：3071-3077.

[16] STRECHA C，HANSEN W V，GOOL L V，et al.On benchmarking camera calibration and multi-view stereo for high resolution imagery[C].2018 IEEE Conference on Computer Vision and Pattern Recognition.IEEE，2008：1-8.

作者信息:

蒋华强1，2，蔡  勇1，2，张建生1，李自胜1，2

（1.西南科技大学 制造科学与工程学院，四川 绵阳621010；

2.制造过程测试技术省部共建教育部重点实验室，四川 绵阳621010）