0 引言

    电机是机器的动力源，随着工业技术的进步，电机也同时向着高性能、高效率、大转矩的方向发展，其控制系统的复杂程度也日益增大。永磁超环面电机是一种结合了行星蜗杆传动与电磁传动的新型电机，它将机械传动、电磁啮合和机电控制结合于一体，降低了控制系统的复杂程度，使得该电机运行平稳，减小了摩擦和噪音，提高了传动效率^[1-2]。永磁超环面电机因其具备行星轮结构的特点，可以在较小的空间范围内传动较大的力矩，这种结构特点使该电机在航天、军事和车辆等要求结构紧凑的领域具有潜在的应用前景。

    永磁超环面电机是一种新型的特种电机，目前国内外对该电机的研究主要集中在电机结构设计优化、工作原理分析和动力学研究^[3-4]。永磁超环面电机控制方法的研究是该电机研究的重要环节，设计合适的控制方法对永磁超环面电机进行调速以达到良好的控制效果，而国内外在此方面的研究较少，所以对永磁超环面电机控制方法的研究具有重要的意义。近年来，无位置传感器控制技术被提出并应用于电机控制领域。无位置传感器控制技术取消了机械式传感器，该控制技术结构简单、控制精度高。文献[5-6]利用无位置传感器控制技术实现了电机转子位置估算，优化了电机控制技术。无位置传感器控制技术在不增加电机体积和结构复杂性基础上满足控制系统精度，该控制技术适合永磁超环面电机的控制。无位置传感器控制方法有扩展卡尔曼滤波器法、滑模观测器法、反电动势估计法、模型参考自适应^[7]等方法。由于模型参考自适应法控制相对简单、控制精度高，本文设计了基于模型参考自适应的永磁超环面电机无位置传感器控制系统。

    本文在分析永磁超环面电机结构及工作原理的基础上，对该电机电感进行了解析计算，并建立了该电机的模型。设计了永磁超环面电机基于模型参考自适应的无位置传感器控制系统，建立了该控制系统的仿真模型，对仿真结果进行分析，验证设计的控制系统的合理性。

1 永磁超环面电机结构原理

    永磁超环面电机结构如图1所示。永磁超环面电机主要由蜗杆内定子1、行星轮2、行星架转子3和环面外定子4组成。

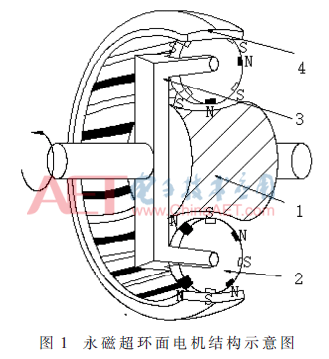
    永磁超环面电机环面外定子由NS极相间的空间螺旋永磁梁相间构成，提供该电机转动的固定磁场。永磁超环面电机转子是由行星架固定的一定数目的行星轮组成的，每个行星轮圆周上均匀分布着NS极相间的永磁体，永磁体个数即为行星轮磁齿数。蜗杆内定子是由硅钢片叠压而成，表面均匀分布有空间螺旋的电枢槽，槽内安放有电枢绕组，通入三相交流电时会产生空间螺旋状的旋转磁场。永磁超环面电机运转过程中，永磁齿受到蜗杆内定子和环面外定子之间的空间磁场的作用，产生的磁场力沿行星轮圆周切线处的分力使行星轮产生自转，沿行星轮轴向方向上的分力使行星轮公转，从而带动行星架转子转动，实现该电机转矩的输出。

2 永磁超环面电机分析建模

2.1 蜗杆绕组电感分析计算

    为了建立永磁超环面电机数学模型，首先对该电机电感进行分析，求得永磁超环面电机电感和行星轮转子位置的表达式。由于永磁超环面电机的结构特殊性，本文将从该电机行星架转子公转方向（设为方向1）和自转方向（设为方向2）来解析建模。蜗杆绕组电感包括绕组之间的自感和互感，应分别分析计算。在蜗杆包角范围内，三相绕组均匀分布，将行星轮自转机械角度展开为电角度，此时永磁齿与绕组的模型可以看成内转子凸极式永磁电机，相邻的一对永磁齿等效为内部永磁转子，建立等效坐标系对绕组电感进行分析计算。等效坐标系建立过程如图2所示。

式中R为蜗杆环面半径，N为永磁超环面电机蜗杆绕组匝数，g为蜗杆与行星轮之间的气隙大小，μ₀为磁导率，l为蜗杆绕组单相线匝长度。

    永磁超环面电机由于蜗杆结构的特殊性，三相绕组在蜗杆上螺旋缠绕，即蜗杆绕组单相线匝长度与蜗杆螺旋升角β有关。蜗杆绕组单相线匝长度为：

2.2 蜗杆绕组与行星轮永磁齿间的互感

    在行星轮自转过程中，永磁齿与绕组的啮合形成磁场周期性的波动，磁场的周期性波动造成蜗杆与行星轮啮合处磁通量的周期性变化，如图3所示。

    当行星轮其中一个永磁齿转动到蜗杆喉部位置时，如图4(a)所示，此时啮合区域磁通量最小。当行星轮转动到如图4(b)所示位置时，啮合区域磁通量最大。永磁齿磁链波动频率与行星轮永磁齿数有关，磁通量的周期变化可以用相应的正旋表达式来表示。行星轮永磁齿磁链大小为：

其中z₀为环面外定子磁齿数。

2.3 永磁超环面电机数学模型

    在以上对永磁超环面电机电感分析基础上，建立绕组为三相十二槽的该电机的数学模型。永磁超环面电机三相静止坐标系下磁链方程为：

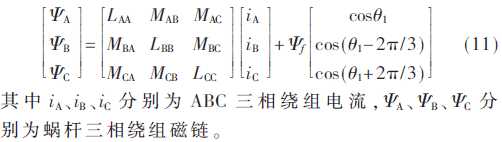
    为了对永磁超环面电机电流进行矢量解耦控制，便于设计该电机无位置传感器控制器系统，需建立该电机位于两相旋转坐标系下的磁链、电压和电磁转矩方程。首先将式(11)中蜗杆绕组磁链方程经过Clark和Park变换：

其中J为永磁超环面电机转动惯量，T_L为该电机加载的负载转矩，B为该电机运转过程中的阻尼系数，ω_m=dθ_1m/dt为行星架转子公转过程中的机械角速度。

3 永磁超环面电机控制系统设计

3.1 基于MRAS的永磁超环面电机控制系统设计

    由于永磁超环面电机输出的电压和电流可以检测，可以通过该电机电压和电流量来估计行星架转子公转的角速度，实现永磁超环面电机的无位置传感器控制。本文设计了永磁超环面电机基于模型参考自适应（MRAS）系统的无位置传感器的控制系统，控制原理如图4所示。

    模型参考自适应系统结构由可调模型、参考模型和自适应律三部分组成^[8-9]。在永磁超环面电机模型参考自适应控制中，把该电机不含有未知参数（行星架转子电角速度）的电压方程表达式作为参考模型，设计含有待辨识参数的电压方程作为可调模型，两个模型具有相同物理意义的电机输出电流。利用参考模型和可调模型的输出量电流误差，通过设计合适的自适应律来实永磁超环面电机行星架转子电角度的辨识。

    对于永磁超环面电机，由式(16)中d-q轴下该电机电压方程改写为：

3.2 自适应律的确定

其中：

    在得到行星架转子公转电角度后，便可求出永磁超环面电机转速，将估计的转速反馈给控制系统，这样便实现了永磁超环面电机的无位置传感器控制。

4 基于MRAS的永磁超环面电机仿真

    在以上理论分析基础上，在MATLAB/Simulink环境下首先用S-Function功能根据式（16）、式（18）、式（19）建立永磁超环面电机模型。在上述设计的基于MRAS的永磁超环面电机无位置传感器控制系统基础上，进行相应的仿真实验。控制系统结构框图如图5所示。

    基于MRAS的永磁超环面电机无位置传感器控制系统采用电流转速双闭环控制，电流环和速度环都采用传统的PI控制。永磁超环面电机无位置传感器控制系统通过MRAS自适应观测器来求得所需反馈信号（行星架转子位置角），进而求得该电机转速，然后将估计的转速与给定转速比较，先经过转速环输出给定q轴电流，再经过电流环得到给定q轴电压，同理得到d轴给定电压，经过空间矢量调制模块，输出合适的脉冲实现永磁超环面电机速度控制。

    设置仿真参数如表1所示仿真参数，建立相应的永磁超环面电机模型及控制系统模型进行仿真实验。

    永磁超环面电机的蜗杆包角大小是主要参数，包角大小决定了该电机结构及输出量大小。下面选择蜗杆包角大小分别为π/2和3π/5的情况进行仿真，分析这两种情况下电机运行状况。仿真条件设置为：仿真时间为0.4 s，额定转速为N^*=600 r/min，空载启动电机，在0.1 s时调速到400 r/min，在0.25 s时施加5 N的负载，得到如图6～图8所示仿真结果。

    由以上仿真结果可以看出：永磁超环面电机转速有较小的波动，这是由于在电机转动过程中，行星轮永磁齿与蜗杆绕组的电磁啮合造成的。永磁超环面电机启动过程中转速误差和行星架转子位置误差较大，当该电机达到稳态运行后，转速估计误差与行星架转子位置角误差逐渐减小。永磁超环面电机降低转速调速过程中，该电机转速估计值有较小的波动。永磁超环面电机平稳运行突加负载后，控制系统仍能很好地对行星架转子位置角进行估计，转速波动幅值较小，并能很快回到稳态运行。不同包角情况下该电机仿真趋势一样，但蜗杆包角变大会导致永磁超环面电机转速波动变大，行星架转子位置估计误差变大。

    仿真结果说明：设计的基于MRAS的永磁超环面电机无位置传感器控制系统可以有效地检测行星架转子位置角，控制系统在不同的转速情况下都有良好的转速跟踪能力，该控制系统有良好的动态和静态性能。

5 结论

    本文在研究永磁超环面电机结构与原理基础上，对该电机的电感进行了解析计算，在此基础上建立了该电机的模型。设计了永磁超环面电机基于MRAS的无位置传感器控制系统，进行了该控制系统仿真实验。仿真结果表明建立的基于MRAS的无位置传感器控制系统可以较好地对永磁超环面电机转速和行星架转子公转电角度进行估计，该控制系统较好地实现了永磁超环面电机无位置传感器控制，为永磁超环面电机控制系统的设计提供了理论指导。

参考文献

[1] 郝秀红，许立忠，郑大周.机电集成超环面传动系统强非线性振动研究[J].中国机械工程，2010，21(19)：2278-2284.

[2] Xu Lizhong，Huang Jin.Torques for electromechanical integrating toroidal drive[J].Proceedings of the Institution of Mechanical Engineers：Part C-Journal of Mechanical Engineering Science，2005，219(8)：801-811.

[3] 许立忠，高艳霞.机电集成超环面传动非线性机电耦合动力学研究[J].燕山大学学报，2013，37(1)：15-21，44.

[4] 郑大周，许立忠，李雯，等.机电集成超环面传动的驱动原理[J].机械设计与研究，2008(3)：43-45.

[5] 杨灵艺，王忠庆.永磁同步电动机参数在线辨识的无位置传感器控制[J].实验室研究与探索，2018，37(2)：104-107，127.

[6] 白洪芬，朱景伟，秦俊峰，等.基于变结构模型参考自适应的双绕组永磁容错电机转子位置估计算法[J].控制与决策，2018，33(1)：27-36.

[7] 曹广忠，黄苏丹，汪济欢，等.平面开关磁阻电机模型参考自适应位置控制[J].电机与控制学报，2016，20(6)：1-8.

[8] 陈炜，张志伟.基于自适应滑模观测器的永磁同步电机无位置传感器控制[J].电工电能新技术，2016，35(8)：8-14.

[9] 邱腾飞，温旭辉，赵峰，等.永磁同步电机控制参数设计方法[J].电工电能新技术，2016，35(6)：60-66.

作者信息:

刘  欣，蔚旭峰

（天津工业大学 天津市现代机电装备技术重点实验室，天津300387）