文献标识码: A
DOI:10.16157/j.issn.0258-7998.183273
中文引用格式: 吴宇豪,安籽鹏. 面向图像三维重建的无人机航线规划[J].电子技术应用,2019,45(3):76-79,87.
英文引用格式: Wu Yuhao,An Zipeng. UAV route planning for image 3D reconstruction[J]. Application of Electronic Technique,2019,45(3):76-79,87.
0 引言
随着无人机技术的发展,无人机被应用到越来越多的领域,例如搜索或探索[1]、震后灾害分析[2]以及森林、矿山、空气质量监测[3]等活动中。利用无人机拍摄地面影像进行三维重建是一种典型的应用。为了完整重建出任务区域的三维模型,首先要解决的问题是合理规划出覆盖任务区域的航线。该问题属于覆盖路径规划问题的范畴。覆盖路径规划问题(coverage path planning)的目的是找到一条路径,以完全遍历任务区域。
目前,国内外学者对覆盖路径规划问题进行了大量的研究,针对不同的应用场景提出了不同的解决方案,主要的应用场景有机器人军事侦察[4]、无人机自动搜索[5]植保无人机农田灌溉[6]等。其中,各应用中的覆盖路径规划算法大致可分为单元分解法与栅格法两种类型。单元分解法中的最为经典的算法是LATOMBE J C在1991年提出的Trapezoidal分解法[7],对整个任务区域进行分割,形成多个子区域,分别进行路径规划。HUANG W H等人[8]对精确单元法提出了改进,提出了“Minimal Sum of Altitude(MSA)”算法。其主要思想是使得覆盖路径中的转弯次数达到最小,以减少在转弯时消耗的能量。栅格法最早由ELFES A和MORAVEC H P提出[9-10],是将覆盖区域均匀划分的方法,目标是寻找一条或多条遍历有效栅格的覆盖路径。其中比较有代表性的算法有基于生物激励神经网络的栅格法[11]、基于生成树的栅格法[12]以及基于四叉树的方法[13]。杨丽春[14]基于改进人工势场法实现了无人机在线航线规划。
针对无人机序列影像三维重建的特定要求,本文主要在不考虑气象因素的条件下研究了凸多边形任务区域的无人机覆盖航线规划问题。融合栅格法的等分思想与扫描航线的特点提出了基于光栅法的无人机扫描航线规划方法,并通过计算最佳扫描方向,使得转弯次数最少化且功耗最小。
1 面向图像三维重建的无人机航线规划问题
1.1 三维重建图像要求
无人机序列影像的三维重建质量主要受到以下因素影响:
(1)重叠度:无人机所拍摄的序列影像需要具有一定的重叠区,即具有一定的旁向与纵向重叠度。一般来说,序列影像的重叠度越高,三维重建的质量越高。
(2)时间连续性:由于环境因素会随时间产生变化,从而导致任务区域的表面特征发生改变。因此,为了获得更好的重建结果,需在尽可能短的时间内完成序列影像的获取。
为了对任务范围进行完整的三维重建,需要规划设计一条或多条无人机全覆盖航线并且所拍摄的序列影像尽可能满足上述条件。
1.2 任务航线规划方式
序列影像满足重叠度要求后,航线规划过程中最需要解决的问题是如何最大限度地降低功耗。无人机航线距离越长,任务所需的时间越长,消耗的能量也会越多。同时,文献[8]提出在相同任务航线距离情况下,转弯次数越多,所耗费的时间将会越长,能量越多。其原因为无人机转弯时需要经过减速、变向、加速等过程,相较于直线飞行会花费更多的时间与能量。
扫描式航线是一种解决全覆盖问题的典型覆盖方法,具有航程较短、转弯次数少等优点。其主要飞行方式如图1所示,无人机起飞之后,按一定的航向沿直线飞行,到达转向点后转向,随后按与之前航向平行但相反的方向飞行至下一转向点,依次循环覆盖任务区域。飞行过程中,设定相机方向为竖直向下,成像角度在整个飞行过程中不变。每一张无人机图像所拍摄的区域实际宽为w,长为l。相邻两张相片之间的旁向重叠度为v,纵向重叠度为h。
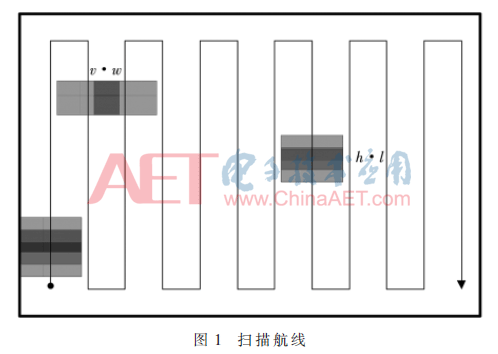
2 覆盖凸多边形任务区域的扫描航线
2.1 基于光栅法的扫描航线规划方法
无人机实际作业的过程中,任务区域往往是不规则的多边形,其中凸多边形区域是较为常见的一种。针对凸多边形任务区域,重点考虑序列图像的重叠度要求,本文提出融合栅格法等分思想与扫描航线特点的光栅法,如图2所示,其规划过程如下。
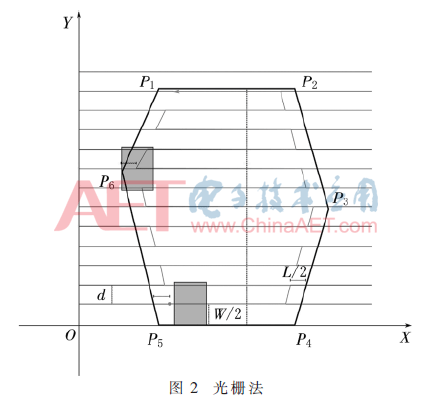
任务区域为多边形P1P2P3P4P5P6。为了便于规划全覆盖扫描航线,建立坐标系XOY,设定坐标系X轴为任务区域多边形某一边(图2中边P4P5),并将整个任务区域多边形置于第一象限内。记任务区域多边形的顶点Pi的坐标为(xi,yi),其中X方向与Y方向坐标的最大最小值分别记为(xmin,xmax,ymin,ymax),任务区域的边界PiPi+1可表示为(y-yi+1)(xi-xi+1)=(x-xi+1)(yi-yi+1),i=(1,2,…,6)。以X轴方向为无人机飞行的起始航向,无人机扫描航线的航线间距d由旁向重叠度v与无人机图像视场宽度w确定,计算方式具体如下式:

以无人机扫描航线的航线间距d作为光栅法的光栅间距,以垂直于无人机起始航向的方向为划分方向,从距离任务区域多边形底边w/2处起等分坐标系第一象限。其中,任务区域多边形覆盖的光栅带为有效光栅带,其余为无效光栅带。扫描航线的匝数n取决于航线间距d、无人机图像视场宽w以及扫描方向长度ls(ls=ymax-ymin):


2.2 最佳扫描方向
由于无人机在转弯时飞行速度会减慢,并耗费大量的能量,减少转弯次数能够有效减少飞行时间,增强序列图像之间的时间连续性并降低飞行功耗。由式(2)可知,扫描航线匝数取决于扫描方向ls的长度,因为航线间距d由图像与重叠度固定确定。因此,最小化扫描方向ls的长度,可以使无人机扫描航线的转弯次数最少化,飞行时间最少,功耗达到最小。
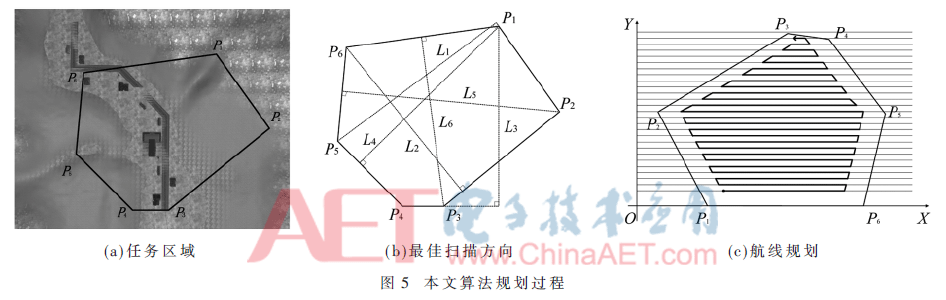
传统的航线规划算法在确立最佳扫描方向时采用枚举的方式进行,设定计算步长r°,航向角α的取值为(0°,r°,2r°,…,nr°,180°),取其中匝数最少的作为最优航线。该方法作业效率低,且精度与步长r°的取值有关。为了确定最佳扫描方向获得最小化的航线匝数,本文提出垂线法以确立最佳扫描方向,如图3所示。
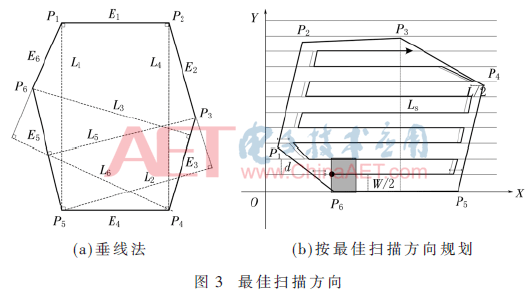
如图3(a)所示,分别计算任务区域多边形各边到最远顶点的距离Li,i∈(1,2,…,6)。其中,选取距离最短的方向作为最佳扫描方向,因为此方向所需要转弯的次数最少,能够最大限度减小无人机功耗,提高任务效率。选取最佳扫描方向,按照2.1中光栅法对任务区域进行扫描航线规划,结果如图3(b)所示。按照最佳扫描方向规划航线得出的最佳覆盖航线的匝数比2.1节中规划的航线匝数少了3匝,转弯数减少,说明按照最佳扫描方向规划航线能够有效减少无人机的功耗。
3 实验验证
本文基于Gazebo仿真平台设计实验验证本文算法的可行性。Gazebo仿真平台提供了多种无人机模型,如AscTec Hummingbird、AscTec Pelican、AscTec Firefly等。该平台同时附带多类型的模拟传感器,如IMU、测距传感器、视觉传感器等,可模拟安装在无人机模型上。为证明本文算法所得到的航线较传统算法的规划航线更加有效,统计对比了两种算法所得航线的转弯次数、航程距离等参数。
实验过程中,构建仿真环境,如图4所示,依照DEM构建基本地形,并添加树木、房子等地物。仿真无人机采用AscTec Firefly六旋翼无人机,并携带视觉传感器。设定无人机航高为50 m,视场宽度w=170 m,长度l=255 m,旁向重叠度h=80%,纵向重叠度v=70%。按顺序选取任务点{P1,P2,P3,P4,P5,P6},连接各点构成任务区域,如图5(a)所示。

(1)传统扫描式航线规划算法
按照传统扫描航线的规划方式,设定航向角α的计算步长为10°,取值范围为(0°,10°,20°,…,170°,180°)。统计不同航向角时,航线的匝数与航程距离,部分统计结果如表1所示。
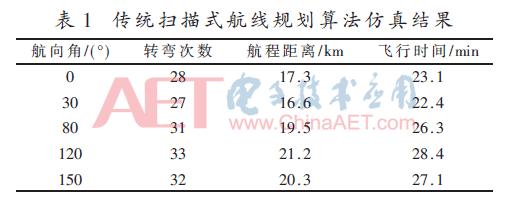
仿真结果显示,当航向角为30°时,航线的转弯次数、与航程距离、飞行时间达到最优。
(2)本文算法

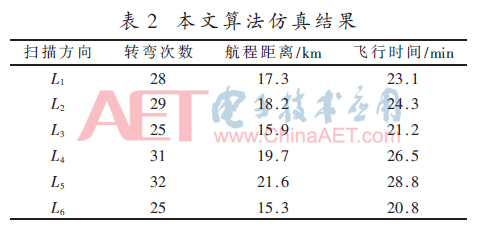
对比传统扫描式航线规划算法与本文算法的仿真实验结果,本文算法能够得出转弯次数最少、航程距离更短、飞行时间更少的航线。在确保序列影像重叠度的情况下,无人机按照本文算法得到的航线飞行时的飞行时间更短、功耗更小,所获得的序列影像时间连续性更强。
借助开源三维重建库openMVG(open Multiple View Geometry)对所拍摄的无人机序列影像进行三维重建,分别生成稀疏点云、稠密点云以及贴合纹理的三维模型,如图6所示。通过观察模型,发现整个任务区域得到了完整的三维重建,贴合纹理的三维模型能够展现任务区域的表面特征,证明本文算法规划的扫描航线能够用于图像三维重建。

4 结束语
新形势下,面向无人机序列影像三维重建的覆盖航线规划问题尤为重要。本文针对凸多边形任务区域,提出了无风环境下面向无人机序列影像三维重建的覆盖航线规划算法。该算法的主要创新内容有两个方面:(1)结合栅格等分思想,提出基于光栅法的扫描航线规划方法,确保了序列影像之间的重叠度要求;(2)提出垂线法用于寻找最佳扫描方向,确保了无人机序列影像之间具有较好的时间连续性,同时使得无人机的飞行功耗更小。
通过搭建仿真环境,实验验证了本文算法得出的扫描航线能够完全覆盖任务区域,得到的航线要优于传统航线,所拍摄的序列影像满足整个任务区域三维重建的要求。为系统研究实际环境下面向图像三维重建的无人机航线规划问题,今后的工作将进一步考虑地形、风速、风向、单架次无人机最大飞行距离等因素对航线规划问题的影响。
参考文献
[1] BALIYARASIMHUNI S,SOUSA J B,PEREIRA F L.UAVs and AUVs coordination for ocean exploration[C].Oceans.IEEE,2009.
[2] XU Z,YANG J,PENG C,et al.Development of an UAS for post-earthquake disaster surveying and its application in Ms7.0 Lushan Earthquake,Sichuan,China[J].Computers & Geosciences,2014,68:22-30.
[3] WATTS A C,AMBROSIA V G,HINKLEY E A.Unmanned aircraft systems in remote sensing and scientific research:classification and considerations of use[J].Remote Sensing,2012,4(6):1671-1692.
[4] 于驷男,周锐,夏洁,等.无人机协同搜索区域分割与覆盖[J].北京航空航天大学学报,2015,41(1):167-173.
[5] WAGNER A,ARKIN R C.Multi-robot communication-sensitive reconnaissance[C].IEEE International Conference on Robotics and Automation,2004.Proceedings.ICRA.IEEE,2003,5:4674-4681.
[6] 徐博,陈立平,徐旻,等.多作业区域植保无人机航线规划算法[J].农业机械学报,2017,48(2):75-81.
[7] LATOMBE J C.Exact cell decomposition[J].The Springer International Series in Engineering and Computer Science,1991,124:200-247.
[8] HUANG W H.Optimal line-sweep-based decompositions for coverage algorithms[C].IEEE International Conference on Robotics & Automation.IEEE,2001.
[9] ELFES A.Sonar-based real-world mapping and navigation[J].IEEE Journal on Robotics & Automation,1987,3(3):249-265.
[10] MORAVEC H P,ELFES A.High resolution maps from angle sonar[C].IEEE International Conference on Robotics and Automation,1985:116-121.
[11] HODGKIN A L,HUXLEY A F.A quantitative description of membrane current and its application to conduction and excitation in nerve[J].The Journal of Physiology,1952,117(4):500-544.
[12] GABRIELY Y,RIMON E.Competitive on-line coverage of grid environments by a mobile robot[J].Computational Geometry:Theory and Applications,2003,24(3):197-224.
[13] 李宏超,黄亚楼,阙嘉岚,等.基于四叉树环境模型的轮式移动机器人平滑路径生成方法[J].机器人,2001,23(5):426-430.
[14] 杨丽春,顾颖彦,白宇.基于改进人工势场法的无人机在线航路规划算法[J].电子技术应用,2018,44(4):5-9.
作者信息:
吴宇豪,安籽鹏
(信息工程大学 地理空间信息学院,河南 郑州450000)

