0 引言

    无人机(Unmanned Aerial Vehicle，UAV)^[1]由于其机动灵活、操控简单、功能性强，近几年引起国内外各高校以及科研机构的广泛关注。作为无人机的一种，四旋翼飞行器结构简单、体积小、重量轻、成本低、易于维护，尤其是那些能够在狭小的空间里完成垂直起降的微型无人机^[2]，广泛应用于农业、工业、军事等各个领域。

    现阶段在UAV领域内设计出了众多控制系统并在实际模型中得到验证。文献[3]提出一种基于传统PID控制方法的飞行器姿态控制系统，控制简单，计算速度快，但是只能在低动态状态下保证良好的工作性能，长时间运行陀螺仪的漂移现象比较严重。文献[4]设计了一种PI-PD控制方式，其中PI控制器能够使系统快速且无稳态误差地收敛，PD控制器可以有效抑制系统超调量，同时克服了PID控制器参数不易整定的缺点，但在响应时间和鲁棒性方面仍有待提高。文献[5]提出一种不完全微分PID控制算法，在常规PID控制器中微分环节的输出串联一阶惯性环节，滤波微分信号，消除高频干扰。目前四旋翼飞行器控制领域开展的研究较少涉足抑制外界干扰以及对系统自身控制误差的补偿，已应用到实物的抗扰算法也不能很好地达到稳定的控制效果。

    本文针对目前普遍采用的传统串级PID控制算法对非线性系统的控制品质较差、鲁棒性弱且对于外界扰动的抵抗能力差等缺点，提出自抗扰PID四旋翼飞行器控制方法，将系统未建模动态和未知外扰动都归结为对系统的“总扰动”进行估计并基于补偿^[6]，提升控制器的品质。

1 四旋翼飞行器动力学模型

    四旋翼飞行器的研究要涉及两个坐标系，E(x_E，y_E，z_E)表示地面坐标系，B(x_B，y_B，z_B)表示机体坐标系^[7]，M1、M2、M3、M4为4个电机，坐标系如图1所示。

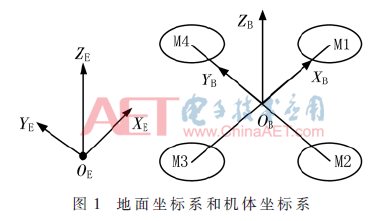
    在实际的飞行环境中，四旋翼飞行器往往会受到气流的影响，随机性和不确定性较大，为了简化模型，对四旋翼飞行器做出如下假设：

    (1)将整个四旋翼飞行器的机体视为一个刚体；

    (2)四旋翼飞行器机体的几何中心和重心是重合的；

    (3)在低速平稳状态下，忽略机身运动时空气动力产生的力和力矩。

    由此对四旋翼飞行器建模如下式：

2 自抗扰PID控制器

    韩京清在20世纪末提出了自抗扰控制（Active Disturbance Rejection Control，ADRC）技术，该方法解决了传统PID控制的超调量和响应速度之间的矛盾，其抗干扰能力强，响应速度快^[8]，控制算法简单，不需要被控对象建立精确的数学模型，也不需要对外界干扰进行建模与测量。

    自抗扰控制器由跟踪微分器、扩张状态观测器和状态误差反馈控制规律三部分组成。本文结合四旋翼飞行器的动力学模型，设计四旋翼飞行器的自抗扰PID控制器，对3个欧拉角(俯仰角、偏航角和横滚角)进行控制，并使自抗扰控制部分对外界的干扰和控制误差进行补偿，其控制系统的结构如图2所示。

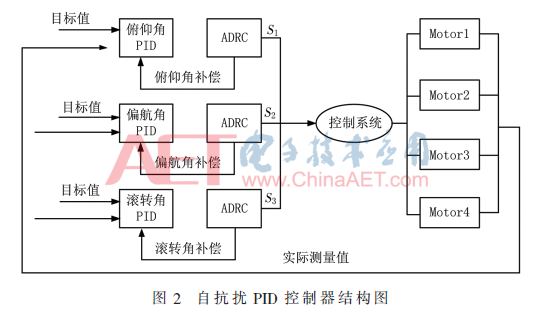
    图2中，S₁、S₂、S₃为自抗扰控制器的输出，实际上3个欧拉角之间是存在耦合关系的，但当四旋翼飞行器处于悬停状态或者运动角速度较小时，可将这种耦合关系忽略，使模型理想化，此时控制器可实现分别对3个状态量进行独立通道控制，当3个欧拉角之间的耦合关系可以忽略不计时，每个通道的控制方法基本类似，现以俯仰角的控制通道为例，介绍飞行控制器的设计。俯仰角控制通道的结构示意图如图3所示。

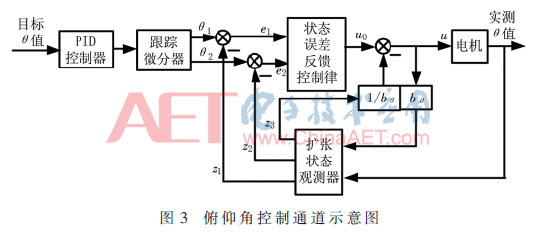
2.1 跟踪微分器

    跟踪微分器中的θ₁是跟踪微分器对于其输入信号的跟随，θ₂是θ₁的微分。微分跟踪器用于安排过渡过程以解决PID控制器中响应速度和超调量之间的矛盾，设计的跟踪微分器具体形式如下：

式中，a为跟踪微分器的速度因子，也就是输出信号的最大加速度；θ₀为微分跟踪器的输入信号，θ₁为跟踪微分器的输出信号，θ₂为跟踪微分器的中间状态变量；h为运算步长；fhan为最速控制综合函数。fhan(θ₁，θ₂，r，h)的计算公式如下式：

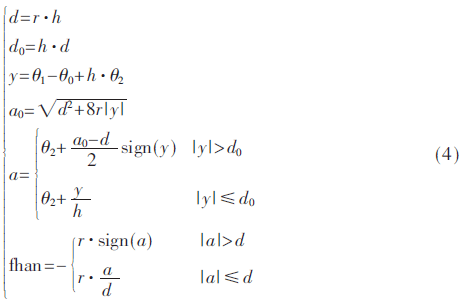
其中，r为快速因子，r越大跟踪速度越快，容易造成超调现象；r越小跟踪过程越长，系统实时性变差^[9]。r和h是跟踪微分器中两个参数，均与过渡过程的快慢和系统的承受能力有关。d和d₀为稳定参考值，y为输出信号。

2.2 扩张状态观测器

    扩张状态观测器将整个系统输出的扰动作为扩增的系统状态，以特定的反馈机制建立观测器来估计这种输出扰动，从而在四旋翼飞行器这种非线性系统的误差反馈环节来消除上述扰动。建立俯仰角通道的扩张状态观测器如下所示：

2.3 状态误差反馈控制律

    状态误差反馈控制律的作用是对扩张状态观测器中的扰动估计值进行补偿，此处采用PID形式对误差进行调节控制，其控制表达式为：

    对误差反馈控制量u₀用ESO对θ的估计值z₃的补偿来决定俯仰角控制通道最终的控制器输出总量为：

式中，b_θ为执行放大系数。

3 仿真分析

    用MATLAB对四旋翼飞行器传统串级PID控制器和自抗扰PID控制器分别进行仿真分析。在Simulink里分别搭建两种控制器的数学模型，对两种控制器输入相同的单位阶跃信号，并在某一时间给予一定的干扰，在scope中分别观察两种控制器的单位阶跃响应，通过对曲线特性的分析，比较两者的优劣。

    经过反复的参数整定，最优控制参数使传统串级PID控制器的输出波形达到最佳状态，如图4所示。同理，在Simulink中搭建自抗扰PID控制器的数学模型，待其参数反复调整到最优，其控制器的输出波形如图5所示。

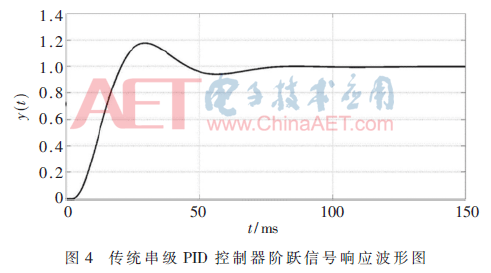
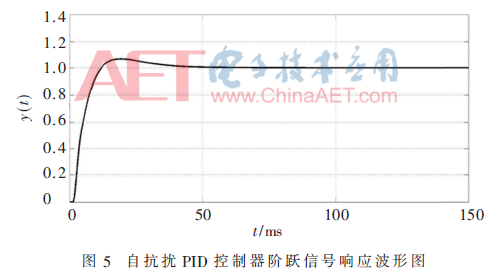
    两幅输出波形图都是在各控制器的参数整定到最佳状态后显示的波形状态，从图形可以看出自抗扰PID控制器的响应速度较传统串级PID控制器提高约30%，稳态误差降低15%，超调量降低20%。在仿真过程中为了验证自抗扰PID控制器的抗扰能力，在两幅波形图达到稳定状态后70 ms的位置给予幅度相同的外界扰动，从波形图可以看出传统PID控制器的波形有轻微的波动，而自抗扰PID控制器的波形基本无波动，从而验证了自抗扰PID控制器有较好的抵抗外界干扰的能力。

    通过对两种控制器输出波形的比较，发现自抗扰PID控制器的控制特性要明显优于传统串级PID控制器。由此得出，在四旋翼飞行器的控制器的设计中，采用自抗扰PID控制算法可以使控制器的整体效果明显得到提升，使其由于系统的鲁棒性和非线性带来的控制的不确定性得到明显的改善。

4 结论

    本文在传统PID控制器的基础上结合自抗扰控制技术提出一种自抗扰PID控制方法，用MATLAB分别对传统PID控制器和自抗扰PID控制器进行仿真，通过对两种控制器输出波形的比较，发现自抗扰PID控制器在响应速度、稳态误差和超调量方面明显优于传统PID控制器。因此得出结论，自抗扰PID控制算法可以使控制效果明显得到提升，能够达到抑制外界干扰以及补偿系统控制误差的效果。

参考文献

[1] 申珊颖.斜十字四旋翼飞行器实验建模与控制计数研究[D].南京：南京航空航天大学，2013.

[2] ZUO Z，ZHU M，ZHENG Z.Trajectory tracking control of a quadrotor unmanned mini-helicopter[C].48th AIAA Aero-space Sciences Meeting Including the New Horizons Forum and Aerospace Expositio,2010.

[3] 叶树球，詹林.基于PID的四旋翼飞行器姿态控制系统[J].计算机与现代化，2015，25(5)：117-120.

[4] 唐健杰，王鑫.基于PI-PD控制器的四旋翼姿态控制[J].电子技术与软件工程，2014，3(16)：175-176.

[5] 薛佳乐，程珩.基于串级PID四旋翼飞行器控制系统研究[J].电子技术应用，2017，43(5)：134-137，142.

[6] 韩京清.从PID技术到自抗扰控制技术[J].控制工程，2002，9(3)：13-18.

[7] 白敬洁.四旋翼飞行器的滑模控制算法研究[D].哈尔滨:哈尔滨理工大学，2015.

[8] 戴启浩，马国梁.四旋翼飞行器的自抗扰控制方法研究[J].计算技术与自动化，2017，36(2)：46-50.

[9] 姜海涛，常青，王耀力.改进EKF的自抗扰飞控系统设计[J].电子技术引用，2018，44(4)：18-22.

作者信息:

张小明1，于纪言1，王坤坤2

（1.南京理工大学 机械工程学院，江苏 南京210094；2.河海大学 能源与电气学院，江苏 南京210094）