0    引言     

SHAMIR A^［1］和BLAKELY于1979年分别提出了秘密共享的概念，其主要思想是在n个参与者之间分享一个秘密，k个(或k个以上)参与者可以恢复秘密，而少于k个参与者则无法恢复秘密，所以，秘密共享也称为(k,n)门限方案。可视密码^［2-3］是一种依靠人眼解密的秘密共享方法，它是将一个秘密图像加密成n张分存图像，n张分存图像可以打印到胶片上、存入电脑或移动存储器中，且分别由n个人保存。解密时只需k个人(或k个以上)将各自的分存图像叠加，秘密图像就会呈现出来，而少于k个人无法获得秘密图像的一点信息。

传统可视密码方法都是使用像素扩展的方法来进行加密，因此使得分存图像被扩展为秘密图像的好多倍，这样不但造成存储空间的浪费，也使得携带更为不方便。

在传统(k,n)可视密码中，秘密图像中的每个像素都单独处理，由n个人共享，每个共享由m个黑白子像素组成。构建一个n×m布尔矩阵B=［B_ij］，当且仅当B_ij=1时第i个共享者的第j个子像素为黑；当且仅当B_ij=0时第i个共享者的第j个子像素为白。当把投影片叠放在一起时，就相当于对于每一行都做了或运算。叠放后图像的灰度值与进行或运算之后的向量V的汉明重量H(V )成正比。使用者利用视觉系统解释灰度值如下，如果H(V )≥d该点像素为黑，如果H(V )≤d-αm该点像素为白。

1    像素不扩展的方案

ITO R^［5］等人针对黑白可视密码提出了一种不扩展的(k,n)-threshold可视密码方案，当要分享一个黑(白)点时，便从对应于黑(白)点的基础矩阵中随机选择列，并且将这个列向量的第i行分配给第i个分存图像。由于不论是黑点或白点的基础矩阵，其每一行0与1分布的比例都相同，因此分存图像上每一个像素，会填上黑点或白点的几率也都一样，依次无法从分存图像上猜测到有关秘密图像的信息。而还原图像则靠式(1)来产生对比。在式(1)中，p₀和p₁分别代表白点和黑点在叠加图像上产生黑点的概率。只要这两个概率值差别够大，人眼便可自动区分叠加图像上黑色与白色的区域。

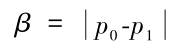(1)

ITO R^［5］等所提出的不扩展模型，在分享一个像素时，是完全随机地从基础矩阵中选择行，虽然在整张叠加图像上，能够达到式(1)的对比，但是在小区域上，黑点与白点的分布就可能无法达到式(1)的对比。侯永昌等人提出了像素不扩展之灰阶密码方案^［6］及像素不扩展之彩色视觉密码技术^［7］，其提出m点同时加密的概念，即用m点同时加密来保证分存图像的像素不扩展。

2     举例说明m点加密

因为基础矩阵B_m×n的列数m=2，所以选择秘密图像上的连续两个点为加密对象，称这两点为加密序列，加密方法如下：

(1)当加密序列为两个白点时用矩阵M₀加密，保证两个分存图像叠加后，此两点为一黑一白；

(2)当加密序列为两个黑点时用矩阵M₁加密，保证两个分存图像叠加后，此两点全黑；

(3)当加密序列为一黑点一白点时，一半用矩阵M₀加密，一半用矩阵M₁加密。保证两个分存图像叠加后，此两点或者是一黑一白，或者是全黑，且这两种情况各占一半。

通过总结，得到(2,2)可视密码加密规则，其中，e代表秘密图像上已经加密过的黑白各半的加密序列的个数，加密规则如下：

if e mod 2<1

用M₁进行加密

else用M₀进行加密

3     兼顾可用性和可靠性的可视密码最佳方案

侯永昌等人的多点加密可以较好地实现像素的不扩展，但是在解密过程中仍然存在秘密图像的对比度不高的问题。结合侯永昌等人的多点加密，在解密的时候使用算法进行重构，方法是在秘密图像的连续m个点中，如果黑色像素H(V )≥d，则对应m个点像素为黑点，否则m个点为白点。

令B₀与B₁分别代表对应于白点与黑点的n×m基础矩阵，加密序列的长度为m，即一次取秘密图像上的m点来加密，b代表加密序列中的黑点个数(0≤b≤m)，e_b则代表具有b个黑点的加密序列已加密过的个数，加密程序如下：

(1)令e_b=0 for b=1,2,…,m;

(2)由秘密图像中取出尚未加密的加密序列，并计算其黑点个数b;

(3)将基础矩阵B 做列向量随机重排，其中矩阵B 根据下列规则决定：

if eb mod m<b

B=B₁

else B=B₀

(4)e_b=e_b+1;

(5)重复步骤(2)~(4)直到秘密图像上的所有像素都加密完毕。

解密重构过程如下：

①令C为k个分享者的分存图像叠加后的图像，D为C重构后的图像;

②存在整数p、q，使m=p×q，且|p-q|最小;

③对于B中的m像素，计算黑点个数:

for x=p:-1:0

for y=q:-1:0

计算解密图像C中m=p×q个点C((p×i-x),(q×j-y))的黑点个数b

end

end

(4)如果黑点个数大于阈值d,重构图像D对应的m个点为黑点，否则为白点:

for x=p:-1:0

for y=q:-1:0

ifb≥d

D((p×i-x),(q×j-y))=1;

else

D((p×i-x),(q×j-y))=0;

endif

end

end

(5)重复步骤(3)~(4)直到秘密图像上的所有像素都重构完毕。

4    兼顾可用性和可靠性的可视密码最佳方案的实例

以(2，3)可视密码来具体说明本文的方法，(2，3)可视密码的基础矩阵如下：

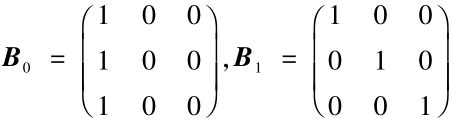
在传统的可视密码中，对于加密图像逐点加密，如果该点为白点，则将B₀进行随机列置换后得到C₀，将C₀的第一行分给第一个分享者，将C₀的第二行分给第二个分享者，将C₀的第三行分给第三个分享者；如果该点为黑点，则将B₁进行随机列置换后得到C₁，将C₁的第一行分给第一个分享者，将C₁的第二行分给第二个分享者，将C₁的第三行分给第三个分享者。这样分享图像和解密图像都将扩大三倍，产生像素扩展。

对于(2，3)可视密码，加密算法为：

(1)令e_b=0 for b=1,2

(2)由秘密图像中取出尚未加密的加密序列，并计算其黑点个数b.

(3)将基础矩阵B做列向量随机重排，其中矩阵B根据下列规则决定：

if    e_b mod 3<b;

B=B₁;

else  B=B₀;

(4)e_b=e_b+1;

(5)重复步骤(2)~(4)直到秘密图像上的所有像素都加密完毕。

图1为加密图像，在加密图像上选取连续3个点，如果3个点中有0个黑点，一直使用B0加密；如果3个点中有1个黑点，则第1次使用B₁加密，后2次这种情况使用B0加密；如果3个点中有2个黑点，则第2次使用B₁加密，后1次这种情况使用B₀加密；如果3个点都为黑点，一直使用B₁加密。使用上面的方法得到分存图像，如图2所示，分存图像没有像素扩展。将任意两个分存图像进行叠加，得到解密图像C，如图3所示，解密图像没有像素扩展。(本文中所有图像都缩小为原图像的50%。)

将解密图像利用算法进行重构，重构过程如下：

(1)令C为k个分享者的分存图像叠加后的图像，D为将C重构后的图像；

(2)存在整数p、q，使3=p×q，且|p-q|最小，则p=1,q=3；

(3)对于B中的3像素，计算黑点个数:

for y=3:-1:0

计算解密图像C中3个点C(i,(3×j-y))的黑点个数b

end

(4)如果黑点个数大于阈值2，重构图像D对应的m个点为黑点，否则为白点:

for y=3:-1:0

ifb≥2

D(i,(3×j-y))=1;

else

D(i,(3×j-y))=0;

endif

end

(5)重复步骤(3)~(4)直到解密图像上的所有像素都重构完毕。

C为解密图像，计算C中连续3个点的黑点个数，如果黑点个数大于等于2，则该点为黑点；否则为白点。得到的重构图像如图4所示，重构图像中没有像素扩展，且有更好的视觉对比度。对于(2,3)可视密码，本方案和其他方案的对比如表1所示。从表1中可以看到，本方案像素无扩展，所以图像也不会有变形，且达到最好的黑白像素对比度。

5     结论

本文在兼顾可用性和可靠性的前提下，提出了实现可视密码的最佳方案，在加密时利用m点加密实现了分存图像的像素不扩展，在解密时利用重构得到更优对比度的重构图像，并以(2，3)可视密码为例说明了该方法的优点。该方法虽然避免了像素扩展且对比度很好，但是解密图像黑色像素边缘会稍有模糊，如何设计更优的像素不扩展算法，是今后需要努力的方向。

参考文献

［1］ SHAMIR A.How to share a secret［J］.Communications.ACM,1979,22(11):612-613

［2］ NAOR M,SHAMIR A.Visual cryptography［J］. Advance in cryptology Euro crypt′94.Lecture Notes in Computer Science,Berlin:Springer,Berlin, 1995,950:1-12.

［3］ DROSTE S.New results on visual cryptography［J］. Lecture Notes in Computer Science, Berlin:Springer-Verlag, 1996,1109:401-415.

［4］ ATENIESE G,BLUNDO C,DE SANTIS A,et al.Visual cryptography for general access structures［J］. Information and Computation,1996,129(2):86-106.

［5］ ITO R, KUWAKADO H,TANAKA H.Image size invariant visual cryptography.IEICE Transactions on Fundamentals of Electronics Communications and Computer Science, 1999, E82-A（10）: 2172-2177.

［6］ 侯永昌,许庆升. 像素不扩展之灰阶视觉密码方法，资管评论，2004，12（13）:107-1240

［7］ 侯永昌.像素不扩展之彩色视觉密码技术［J］.Journal of Information,Technology and Society,2004(1):95-110.

［8］ 乔明秋，朱悦冬，刘焕平.多秘密共享可视密码及在防止欺骗上的应用［J］.哈尔滨师范大学自然科学学报，2007(2):61-65.

［9］ 张舒,艾小川.一种具有理想对比度的可视密码方案［J］. 计算机与数字工程，2015(8)：1462-1464.

［10］ 李春艳,基于像素不扩展视觉密码的水印算法［J］. 大理大学学报,2017(6)：19-21.

［11］ 王洪君,马冬鹤,张恩绮,等.一种无像素膨胀的(3,3)视觉密码方案［J］. 武汉大学学报(工学版),2018(12)：1123-1128.

［12］ 沈刚,付正欣,郁滨.基于XOR的(2，2，n) 多秘密视觉密码［J］. 计算机应用研究，2012(10)：3797-3799.

（收稿日期：2019-01-20）

作者简介：

乔明秋(1982-)，通信作用，女，硕士研究生，讲师，主要研究方向：密码学、信息安全。E-mail: qiaomingqiu@163.com。

赵振洲(1978-)，男，硕士研究生，副教授，主要研究方向：数据恢复、信息安全。