0 引言

    公钥密码体制因其强大的安全性，广泛应用于信息安全领域。椭圆曲线密码算法与RSA相比，具有相同安全性下运算速度更快、占用资源更少、位宽更低的优点，成为新一代的公钥密码体制标准。椭圆曲线密码处理器通常根据每秒钟点乘的计算次数作为衡量其性能好坏的标准之一。实现点乘运算，要大量调用模乘、模除和模加减等有限域层模运算。模除运算最为复杂，耗时最多，通常引入投影坐标系，降低调用次数。而与模乘相比，模加减的运算量几乎可以忽略。模乘是椭圆曲线密码算法中最基本、最核心的一种模运算，提高其运算速度将有效提高椭圆曲线密码处理器性能。

    如今，设计一种灵活高效、适用于多种安全场景的模乘器仍然是研究热点。文献[1]基于CPA和CSA结构实现了的统一的MALU单元，能够有效完成模运算，资源复用率高，灵活性和可扩展性强，但是随着运算位宽的增加，CPA的进位链会成为瓶颈，大大制约着电路的性能。文献[2]采用64位的基4 Kogge-Stone超前进位加法器实现DFA，实现新型的Wallace数乘法单元，缩短了运算时间，但硬件资源占用较多。文献[3]在Blakley算法的基础上，提出改进的Radix-4快速模乘算法，采用Booth编码减少迭代次数，并采用符号估计技术避免大整数比较，还基于扩展Euclidean求逆算法，设计统一硬件电路，虽然面积很小，但是运算速度不高。本文根据基于Radix-4交错模乘算法^[4]，采用进位保留加法器(Carry Save Adder，)和Kogge-Stone加法器(Kogge-Stone Adder，KSA)^[5]组合的加法结构，缩短电路关键路径，同时支持素数域GF(p)和二元域GF(2^m)的模乘运算。根据操作数位宽控制迭代轮数，灵活适配各种长度的模乘运算。

1 背景介绍

1.1 Kogge-Stone加法器

    在硬件电路设计中，基础的加减乘除运算，最终都可以通过多次加法计算来实现，因此加法器是许多运算模块的基础单元，其性能好坏直接关系到整个电路的性能。对于传统加法器，如串行进位加法器、进位选择加法器，高位的计算需要低位的进位输出。随着运算位宽的增加，加法器的进位链不断增长，大大制约着加法器的运算性能。为了减少进位时间，1973年，KOGGE P M和STONE H S提出了并行前缀的超前进位加法器，使高位的计算与前一位的进位结果无关，从而大大提高加法器的速度。

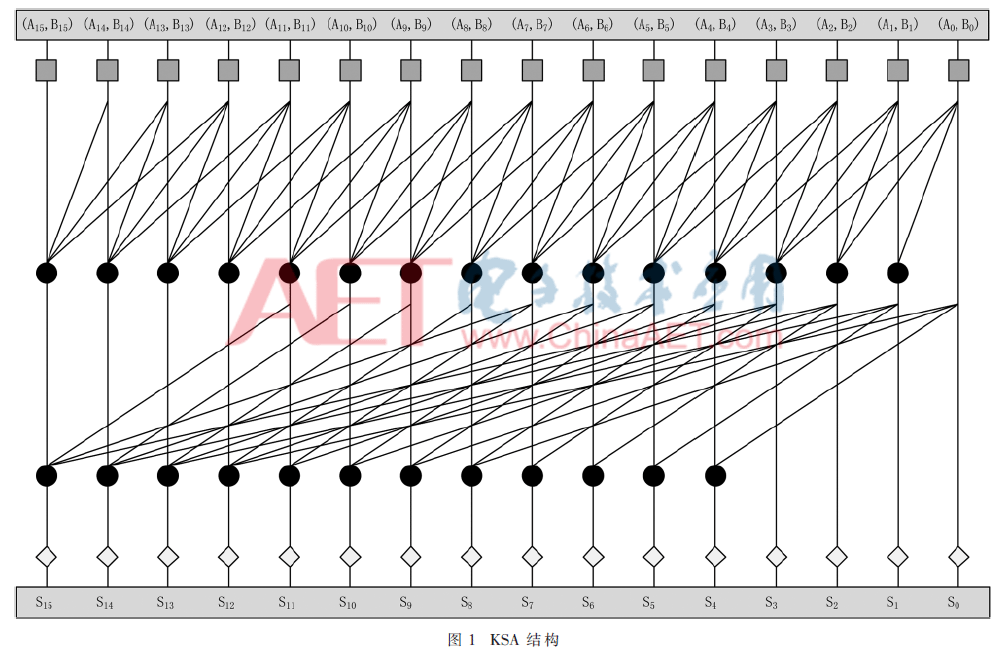
    本文中KSA采用4位一组的点操作，计算延迟是log₄N级点操作的延迟，与普通的二进制KSA加法器结构相比速度提高一倍。图1是以计算16位加法为例的四进制KSA结构^[4]，该结构由三种基本单元构成。最上面的正方型代表前置进位信号产生电路，用于产生进位传播信号P_i和进位产生信号G_i。最下面的菱形表示最终的进位生成电路与求和电路，用于产生每一位的进位信号C_i与加法和S_i。中间的圆形代表Kogge-Stone树结构，用于产生进位信号C_i所需的中间结果，包括块进位产生信号和块进位传播信号。

1.2 进位保留加法器

    进位保留加法器(CSA)常用于多操作数的加法。假设计算三个m比特的操作数A、B和C的和，采用CSA结构，将输出两个结果：本位异或结果sum与进位carry。还需要一个加法器将sum和carry相加，本文中，CSA和KSA共同完成三操作数相加。

    CSA用表达式可以表示为：

1.3 模乘算法分析

    模乘是椭圆曲线密码的核心运算，本文中交错模乘算法如算法1所示，支持素数域GF(p)和二元域GF(2^m)上的运算。

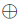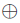    二元域运算与素数域的不同在于二元域运算没有进位，运算更加简单。素数域中的模数P，在二元域中表示为不可约多项式F(x)。模乘素数域用进行2Amod P、4Amod P和x+y+zmod P三种运算，在二元域中表示为x·A(x)mod F(x)、x2·A(x)mod F(x)和xyz。

2 模乘结构

2.1 模乘总体结构

    根据Radix-4交错模乘算法，本文设计了长度可变的双域模乘器，其总体结构如图2所示。实线框内表示素数域的模乘运算单元，长虚线框内表示用于二元域模乘的运算单元。短虚线框中标出的是本结构中的复用部分，一是x²·A(x)modf(x)结构复用了x·A(x)modf(x)结构；二是复用x+y+zmod P结构中的CSA0中三操作数的异或输出sum，实现二元域上的三操作数相异或。

    该结构由运算单元、控制器和中间数据寄存器组成。

    运算单元是双域模乘器的核心部分，主要包括2Amod P结构、4Amod P结构、x+y+zmod P结构、x·A(x)mod f(x)结构和x²·A(x)mod f(x)结构。

    中间数据寄存器主要用于寄存每一轮迭代计算出的U、V、A、B的值，数据选择器选择寄存运算单元的结果。

    控制器基于状态机设计，产生数据路径中数选器的选择信号，以控制数据路径中的数据流向，完成双域模乘运算时各个模块的调度控制。并根据域选择信号以及数据长度，进行判断执行素数域还是二元域运算，以及迭代轮数。

2.2 双域模乘器运算单元

2.2.1 素数域

    （1）2Amod P结构

    实现2Amod P，即完成A左移一位，再判断2A与P的大小决定是否进行“-P”操作，以实现0≤2Amod P<P。由于0≤A<P，则0≤2A<2P，故2Amod P的结果分两种情况：

    2Amod P结构如图3所示，该结构由一个KSA和一个数据选择器组成。KSA主要用来计算2A-P，数据选择器将KSA的进位输出作为数选信号，判断2Amod P的输出结果。

    (2)4Amod P结构

    实现4Amod P，首先A左移两位，再判断4A与P的大小，重复进行“-P”操作直至0≤4Amod P<P。由于0≤A<P，则0≤4A<4P，故4Amod P的结果分四种情况：

    4Amod P结构如图4所示，该结构由1个CSA和3个KSA组成。并行计算4A-P、4A-2P、4A-3P，根据三个KSA的进位输出作为数选信号，选择最后输出结果。

    (3)x+y+zmod P结构

    实现x+y+zmod P，先计算x+y+z，再判断x+y+z与P的大小，重复进行“-P”操作直至0≤x+y+zmod P<P。由于0≤x、y、z<P，则0≤x+y+z<3P，故x+y+zmod P的结果分三种情况：

    x+y+zmod P结构如图5所示，该结构由3个CSA和3个KSA组成。并行计算x+y+z、x+y+z-P、x+y+z-2P，根据KSA1和KSA2的进位输出作为数选信号，选择最后输出结果。

2.2.2 二元域

    二元域不同于素数域，算法更为简单，移位与异或即可实现x乘，将操作数按位异或即可实现加法，无需考虑进位。

    (1)加法结构

    本文中，二元域三操作数异或通过复用x+y+zmod P结构中的CSA0实现。

    (2)x乘结构

    实现x·A(x)mod f(x)，即将A(x)左移一位，如果a_m-1=1，将之与f(x)进行异或。

    其结构如图6所示，将此结构进行级联，即可实现。

3 性能分析

    本文采用Verilog HDL硬件描述语言对双域模乘器进行RTL级描述，并利用ModelSim进行功能仿真验证。在0.18 μm CMOS工艺标准单元库对双域模乘器进行逻辑综合，综合工具使用Synopsys公司的Design Complier。综合结果表明，双域模乘器占用硬件资源66 518 gates，最高时钟可达到476 MHz，计算256 bit的模乘运算仅需0.27 μs。

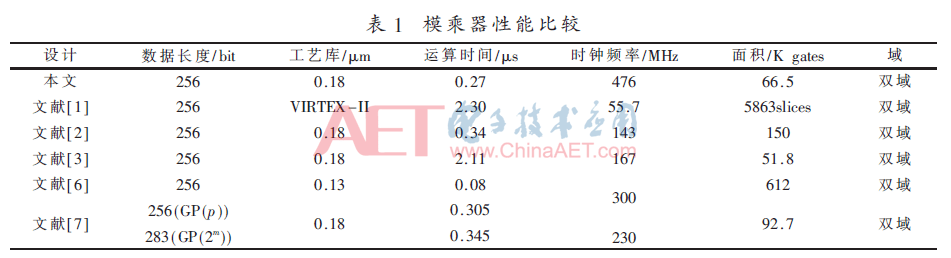
    本文中双域模乘器结构的关键路径在于CSA和KSA组合的加法结构。为了验证模乘器的性能，将本文和其他文献的模乘单元的性能进行比较，其结果如表1所示。本文与文献[2]相比，模乘运算时间降低了20.59%，且面积减小了55.67%。本文的运算时间是文献[6]的3.38倍，但面积大概只有文献[6]的1/10。与文献[3]相比，虽然面积略大，但256 bit的计算时间降低了87.2%。与文献[7]相比，本文速度降低不多，但面积减小了28.26%。综上，本文的双域模乘器在速度和面积上具有综合优势。

    综合比较，本设计能同时支持素数域GP(p)和二元域GP(2^m)的模乘运算，并且适配不同长度的位宽需求，具有较强的灵活性和可扩展性。

4 结论

    本文基于双域Radix-4交错模乘算法，采用CSA和KSA组合的加法结构，实现长度可伸缩的双域模乘器。采用基于Kogge-Stone结构的并行前缀加法器，减小了进位延迟，缩短了该模乘单元的关键路径，大大提高了运算频率，尤其当运算位宽越大，优势越明显时。结构上复用了素数域x+y+zmod P结构的CSA0加法器中的异或门实现二元域中的三操作数的异或，减少硬件资源，提高单元利用率。

参考文献

[1] LIU Z，LIU D，ZOU X.An efficient and flexible hardware implementation of the dual-field Elliptic curve cryptographic processor[J].IEEE Transactions on Industrial Electronics，2017，64(3)：2353-2362.

[2] 郭晓，蒋安平，宗宇.SM2高速双域Montgomery模乘的硬件设计[J].微电子学与计算机，2013(9)：17-21.

[3] 陈光化，朱景明，刘名，等.双有限域模乘和模逆算法及其硬件实现[J].电子与信息学报，2010，32(9)：2095-2100.

[4] 李泉龙.基于Kogge-Stone算法与多米诺逻辑的64位高性能加法电路设计[D].成都：西南交通大学，2016.

[5] KOGGE P M，STONE H S.A parallel algorithm for the efficient solution of a general class of recurrence Equations[J].IEEE Transactions on Computers，1973，C-22(8)：786-793.

[6] 廖望，万美琳，戴葵，等.可扩展双域模乘器设计与研究[J].华中科技大学学报(自然科学版)，2015(9)：51-54.

[7] 李嘉敏，戴紫彬，王益伟.可编程可伸缩的双域模乘加器研究与设计[J].电子技术应用，2018，44(1)：28-32，36.

作者信息:

杨丹阳1，杨  萱2，陈  韬1，戴紫彬1，李  伟1

(1.信息工程大学，河南 郑州450001；2．江南计算技术研究所，江苏 无锡214083)