0 引言

    控制棒是实现反应堆正常启停、功率运行和紧急停止的重要控制装置^[1]。当遇到需要停堆的紧急情况时，控制棒以自由落体的方式快速落下，达到停止反应的安全状态。但是控制棒在落棒期间可能遇到卡棒事故，运行期间可能会出现弹棒事故，因此对控制棒的棒位测量至关重要。棒位测量系统使操作人员能够及时发现控制棒是否按照指定的程序运行和产生故障时的位置，并迅速处理控制棒故障，以确保控制棒的安全运行。控制棒落棒过程为直线下落运动，当使用电容位移传感器测量位移时，能够准确反映电容与位移关系的方程式是知道控制棒在堆芯中位置的关键。

    位移测量传感器^[2-3]按照测量原理可分为电感式位移传感器、电涡流式位移传感器、超声波位移传感器、电容位移传感器等^[4]。其中，电感式传感器和电涡流式传感器在具体实验中虽然具有连续测量、精度较高等优点，但都会有系统复杂且制造困难等问题；超声波传感器具有波长短、频率高、方向性好等优点，但是易受反应堆内环境影响，造成测量困难，会产生不小的误差，且超声波传感器由于置于控制棒外壳内部，使得维修不易。相比较而言，电容传感器具有一定的优越性，它具有可靠性高、响应速度快、测量精度高等优点，且结构简单，使用方便。因此，本文使用电子六所研制的电容式位移传感器对控制棒数据进行研究。

    控制棒落棒过程为直线下落运动，落棒时控制棒位移与电容值之间的关系对精确指示棒位非常重要。本文分别使用三次样条函数、最小二乘法和BP神经网络算法，对位移测量得到的数据进行曲线拟合分析，确定位移与电容值之间的关系。

1 电容式位移传感器测量原理

1.1 三次样条插值拟合原理

1.2 最小二乘法拟合拟合原理

    根据式(4)可知X×L=Y，由于X和Y已知，可根据L=(X′X)^-1X′Y求得L，从而得到拟合曲线。

1.3 BP神经网络拟合原理

    BP神经网络是一种按照误差逆传播算法训练的多层前馈神经网络。通过输入层神经云接收外界输入，隐层与输入层神经元对信号进行加工，然后由输出层神经元输出结果。BP神经网络模型如图1所示。

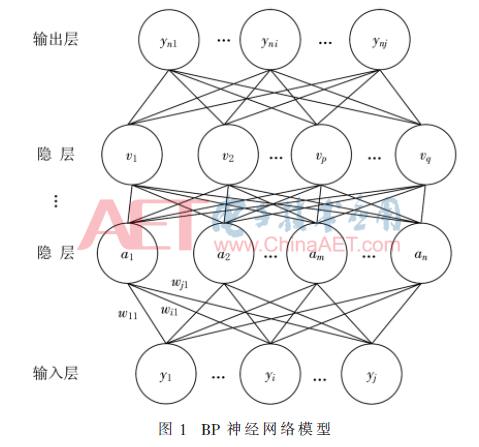
    对于神经网络来说，包含一个输入层、一个输出层、n个隐层(n可以等于任意整数)。每一隐层的神经元都可以看作下一层的输入，其值等于上一层与当前神经元相连的每一个神经元与其权值之积的和，如：

    同理可得V_n(n=1，…，q)的值。 

    BP神经网络的计算流程为将输入实例传送给输入层神经元，然逐层将信号前传，直至产生输出层的结果：

    (1)随机化所有的阈值和连接权；

    (2)计算输出层的误差，将误差反向传播至隐层神经元；

    (3)根据隐层神经元的误差来对连接权和阈值进行调整；

    (4)将步骤(2)~步骤(3)循环进行，直至达到终止条件^[6]。

2 实验与分析

2.1 实验配置

    本次实验采用光栅线位移传感器为位移输入设备，清华大学研发的电容传感器以及与电子六所合作开发的电容测量仪及采集软件作为电容值输出设备。通过控制棒位移的移动对电容值进行数据标定。

    实验配置为：控制棒套筒尾端端子(高低电平和地线)通过线缆与测量仪接口连接，测量仪通过Modbus RS-485串口与个人计算机(PC)上USB口连接，实验配置如图2所示。

    经过标定得测得的电容值经过测量仪测量后保存在PC上，对PC中的数据进行拟合分析。

2.2 实验分析

    标定实验的现场工况为，数据标定的行程为0～840 mm，以15 mm为一步长标定电容值，一组实验标定4次，分别为：(1)控制棒水平放置时，从0 mm～840 mm逐步递增移动；(2)控制棒水平放置时，从840 mm～0 mm逐步递减；(3)控制棒垂直放置时，从0 mm～840 mm逐步递增；(4)控制棒垂直放置时，从840 mm～0 mm逐步递减移动。由于仪器测得的电容值存在波动，非稳定值，因此以上4种情况的每个位置均测量100组电容值，取其平均值，分别得到4组数据。

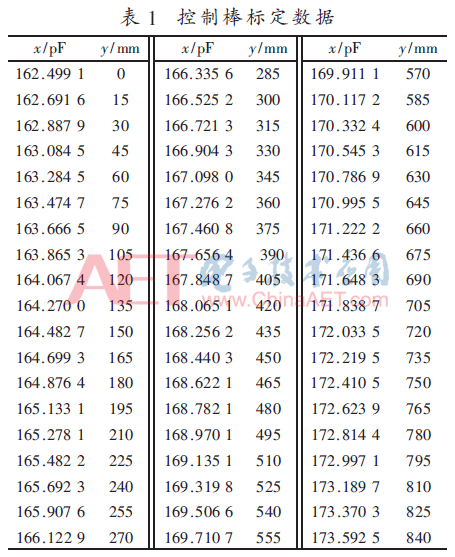
    x表示在同一位移时4种情况电容值的数学期望；y为位移，从0 mm～150 mm，每15 mm为一步。实验数据如表1所示。

    通过残差分析可以看出，拟合精确度大约为0.04，残差分析得到的决定系数R²为0.060 4，统为计量(F值)为2.570 9，F(1，n-2)分布大于F值的概率P为0.116 7。

    图5(a)、图5(b)分别为使用最小二乘法拟合得到的曲线图像，图6(a)、图6(b)分别为实际电容值与拟合电容值之差做出的残差图。其中，data1为使用最小二乘法拟合得到的曲线，data2为验证点(x₂，y₂)的值，data3为x₂通过曲线插值之后得到的拟合点(x₂，)，data4为用于拟合曲线的点(x₁，y₁)。

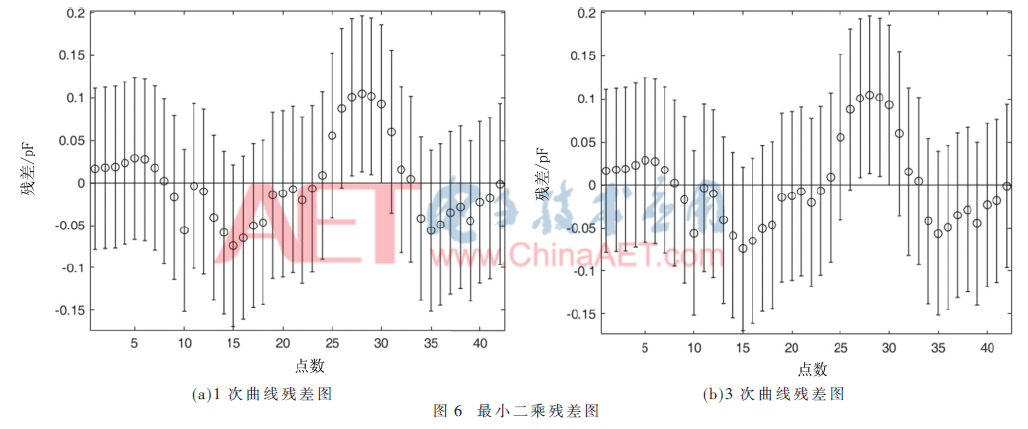
    通过残差分析可以看出，两种函数拟合精确度大约为0.2、0.16，残差分析得到的决定系数R²分别为0.009 5、0.001 0，统计量(F值)为0.383 9、0.039 4，F(1，n-2)分布大于F值的概率P分别为0.539 1、0.843 7。

    一般来说决定系数R²越大，说明回归约显著；概率P越小，说明拟合模型效果越好。所以通过残差分析可以看出与最小二乘法相比，三次样条的拟合效果更好。

    使用BP神经网络进行曲线拟合，设置隐层分别为3、9层，参数迭代次数100次，将(x₁，y₁)值作为训练集，(x₂，y₂)作为验证集和测试集，且验证集和测试集各占50%的比例，分别得到的拟合函数和误差如图7所示。

    从以上试验结果可以看出，隐层次数在3层时，误差不超过0.2；在9层时，误差在2之间。在控制棒标定多次实验中，BP神经网络算法拟合曲线时隐层在3～6时，拟合效果相对更好。虽然利用BP神经网络的学习和泛化能力可以很好地拟合出控制棒棒位移动时位移与电容值之间的特性曲线，但是无法得到确定的某一拟合方程式，在测量仪中实现较为困难，以至于在现场中无法使用，相比较而言，三次样条函数和最小二乘法更易得到拟合曲线。

    在残差分析图中，三次样条函数和最小二乘法均存在异常点，经过分析怀疑是重力原因，由于控制棒在套筒内由于重力原因无法正好在套筒的正中心，可能导致控制棒在移动时稍微向下倾斜，导致存在异常点，暂时无法避免，并且没有好的方法进行验证。

3 结论

    本文使用MATLAB，通过三次样条插值、最小二乘法和BP神经网络三种方法，对控制棒位移测量数据进行了拟合分析。由于与最小二乘法相比，三次样条插值的拟合效果；与BP神经网络相比，三次样条插值更易得到拟合公式，易于插值。综合而言，在反应堆控制棒落棒时，使用三次样条插值得到的函数效果更好。

参考文献

[1] 张涛.基于数字图象处理技术的光学位移测量方法的研究[D].哈尔滨：中国地震局工程力学研究所，2011.

[2] 吴轶，李青，施阁.一种用于地下位移测量传感器串的无线电能传输装置设计[J].电子技术应用，2018，44(7)：155-159.

[3] 焦万果，李昱融，周雯.能量收集认知传感器网络综述研究[J].电子技术应用，2015，44(10)：23-28.

[4] 王晓立.电容式位移传感器研究[D].湘潭：湘潭大学，2010.

[5] SAUER T.数值分析[M].裴玉茹，马赓宇，译.北京：机械工业出版社，2014.

[6] 周志华.机器学习[M].北京：清华大学出版社，2016.

作者信息：

张  菡1，薄涵亮2，王  帅1，杨文龙1，傅一帆1

(1.华北计算机系统工程研究所，北京100083；2.清华大学 核能与新能源技术研究院，北京100084)