文献标识码: A
DOI:10.16157/j.issn.0258-7998.190584
中文引用格式: 汪秋婷,戚伟. 基于缺失观测值的锂电池剩余寿命估计方法研究[J].电子技术应用,2019,45(11):91-95.
英文引用格式: Wang Qiuting,Qi Wei. Research on estimation method of lithium-ion battery remaining useful life based on missing observations[J]. Application of Electronic Technique,2019,45(11):91-95.
0 引言
锂电池广泛应用于机械、计算机和移动设备,其优良性能包括寿命长、能量密度高、效率高、充放电速率快、重量轻、温度范围宽、自放电速率低和无记忆效应等[1]。锂电池剩余寿命预测方法主要分为两大类:基于模型的预测方法和基于数据驱动的预测方法[2]。基于模型的预测方法是应用最广泛的估计方法,但是,由于预测模型的所有参数均需要初始化和预调整,该方法在实际应用中很难获得精确和完善的模型参数[3-4]。基于数据驱动的预测方法可以解决上述问题[5-6],该方法利用电池降解曲线中现在和过去的观测值来预测未来值。现代锂电池健康状况预测系统需要完成短期估计、长期估计和缺少观测值估计等任务,一步超前预测(OSP)用于预测短期电池状态,多步超前预测(MSP)用于预测长期电池状态[7-10]。缺失观测值问题的处理方法包括:(1)状态预测之前,简单地将不完备观测值进行分离,该方法会导致信息丢失和不符合逻辑的估计结果[11];(2)用目标观测值的平均值和中值来代替缺失观测值,该方法可能会导致有偏估计。本文在观测值缺失条件下,对锂电池剩余使用寿命进行估计和预测,创新性地提出基于单点/多重插值技术和一步/多步超前算法的估计策略,主要框架包括预处理模块和预测模块。
1 插值与预测算法


1.2 多步超前预测(MSP)
多步超前预测用于估计电池的长期RUL,该方法分为三大类:迭代法、DirRec法和直接法[13-14]。本文应用DirRec法进行算法改进。
DirRec算法估计L个后续数值的公式表示为[15]:

2 估计方法整体框架
本文提出缺失观测值条件下锂电池剩余使用寿命的有效估计方法,如图1所示,引入传统ELM设计单点和多重插值技术,应用于预处理模块填补缺失观测值;引入传统ELM(ELM)、设计核化ELM(KELM)和在线顺序ELM(OS-ELM),应用于预测模块估计剩余寿命。

2.1 极限学习机
给定一组m个观测值,ELM随机分配输入权重和隐藏层偏差,ELM分析和调整输出权重,算法公式如下:

2.2 核化极限学习机(KELM)
本文基于ELM设计核化极限学习机KELM,该算法利用ELM模型的内核矩阵,并满足Mercer条件,如式(12):

2.3 多步超前预测新算法
本文基于多重插值技术和DirRec法,设计多步超前预测算法的新模型,该模型能够在每个计算步骤之后生成新的预测模型。估计L个锂电池容量的新预测值公式为:

2.4 插值算法和预测算法模型训练
(1)多重插值算法模型训练


(2)多步超前预测方法模型训练
对包含15%缺失观测值的不完备数据集,应用多重插值算法对输入子集进行数据填补,本文应用多步超前估计器,分别结合5种不同插值算法计算RMSE值,如表1所示。该实验选取的不完备数据集包含3个滞后输入值,利用前60%观测值进行模型训练。表1说明:5种插值算法结合不同估计器,预测RMSE平均值相当;KELM-RBF估计器的RMSE均大于其他超前估计器,达到18%,OS-ELM估计器的平均值最小,不超过8.9%;ELMSI与OS-ELM结合,RMSE平均值最小,预测效果最好。

3 实验结果与分析
本文根据剩余寿命估计误差(ERUL)和均方根误差(RMSE)对估计结果进行分析,RMSE分析估计值与真实值之间的差值,ERUL分析锂电池达到终止寿命的实际周期数与估计周期数之间的差值。根据上述实验要求,单体电池B001、B002和B003的电压阈值分别为1.299 V、1.424 V和1.41 V。为了评估新型估计模型的算法性能,在电池老化数据集的各个周期中引入一组缺失观测值,人为创建不完备数据集,该数据集在多重插值算法中被随机导入不同的数据集周期中,特别是训练序列的最后周期导入概率最高。
3.1 模型训练结果比较
利用单体锂电池B001的前40%观测值进行模型训练,训练结果如图2所示,训练模型选取非线性模型、线性模型,并与目标参数真实值进行比较。图2表明,即使利用前40%观测值进行训练,本文提出的ELMMI非线性模型计算结果最接近真实值;同时,锂电池剩余寿命预测过程使用非线性插值算法模型更具优势,该模型可以用有限数量的观测值生成有效的预测模型。

3.2 一步超前预测
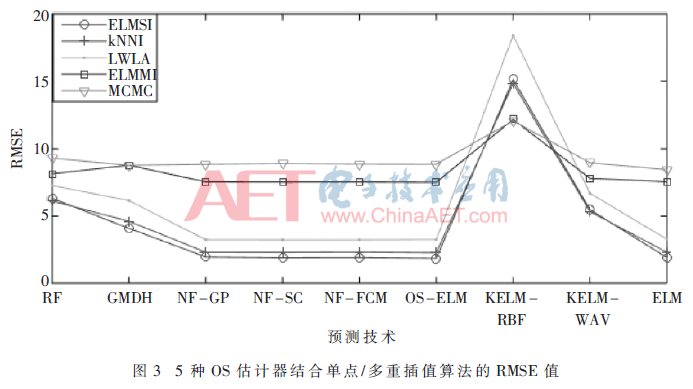
利用单体锂电池B002的前60%观测值进行模型训练,选取5种一步超前估计器(OS),通过单点和多重插值算法接收3个完整的观测序列。图3为5种插值算法结合不同估计器计算得到的RMSE值:(1)使用单点插值算法得到的预测结果,OS-ELM与ELMSI组合时产生最低RMSE值;(2)不同的曲线反映不同插值算法得到的RMSE平均值;(3)ELMSI与多种估计器结合,预测结果与单点插值算法结果相同,KNNI插值算法与 RF估计器、KELM-RBF估计器结合得到最优预测结果;(4)本文提出将多重插值算法ELMMI与不同多步超前预测方法相结合,构建基于多重插值算法的多步超前估计器,能够实现准确和稳定的估计过程。
3.3 多步超前预测
利用单体电池B003的前60%观测值进行模型训练,将多步超前预测算法应用于预测模块,实验利用MSP中的DirRec法计算终止寿命的误差值(ERUL),结果如表2所示:(1)MCMC总体误差值最大,达到45%以上,ELMSI、kNNI和LWLA误差值相当,不超过23%;(2)ELM与不同插值技术结合的估计器平均误差值最小,能够较好地估计锂电池短期和长期剩余使用寿命,且估计器建立时间短、估计精度高;(3)对于一步超前预测过程,OS-ELM和ELMSI(ELMMI)相结合比其他插值算法具有更好的预测性能;(4)多步超前预测的两种核化函数得到的误差值相同;(5)RF估计器建立的预测模型性能较好,但在一步超前预测中该估计器的性能显著下降。

4 结论
本文提出一种缺失观测值条件下锂电池剩余使用寿命的有效估计方法,该方法基于多重插值技术和多步预测算法,设计整体框架包括预处理模块和预测模块。本文创新点包括:(1)提出集成ELM为基础的估计器框架,处理缺失观测值条件下的插值和预测任务;(2)预处理模块中,将ELSMI(ELMMI)与KNNI单点插值算法相比较,结果表明本文提出的插值算法能够为预测模块提供高精度的输入值;(3)在预测模块中,基于ELM设计多种估计器,并与不同的插值算法相结合,实验表明基于ELM的估计器能够得到精确的预测结果。
参考文献
[1] 欧阳明高.中国新能源汽车的硏发及展望[J].科技导报,2016,4(6):13-20.
[2] 孙猛猛.基于数据驱动方法的锂离子电池健康状态估计[D].昆明:昆明理工大学,2018.
[3] BARALDI P,MAIO F D,AL-DAHIDI S,et al.Prediction of industrial equipment remaining useful life by fuzzy similarity and belief function theory[J].Expert Systems with Applications,2017,5(83):226-241.
[4] 汪秋婷,姜银珠,陆赟豪.基于UKF的18650锂离子电池健康状况估计[J].电源技术,2016,40(3):543-546.
[5] RAZAVI-FAR R,FARAJZADEH-ZANJANI M,CHAKRABARTI S,et al.Data-driven prognostic techniques for estimation of the remaining useful life of lithiumion batteries[C].Proceedings of the IEEE International Conference on Prognostics and Health Management(ICPHM),2016:1-8.
[6] 周建凯,许盛之.基于深度学习的电池片缺陷识别研究[J].电子技术应用,2019,45(5):66-69,77.
[7] 高栋,黄妙华,周亚鹏.基于充电电流数据的锂电池容量估计[J].电源技术,2018,42(10):1447-1450.
[8] ACUNA D E,ORCHARD M E,SILVA J F,et al.Multiple-imputation-particle-filtering for uncertainty characterization in battery state-of-charge estimation problems with missing measurement data:Performance analysis and impact on prognostic algorithms[J].International Journal of Prognostics and Health Management,2016,6(3):1-12.
[9] 罗勇,祁朋伟.基于模拟退火算法的锂电池模型参数辨识[J].汽车工程,2018,40(12):1418-1425.
[10] 谢建刚,李其仲,黄妙华,等.锂离子电池剩余容量与剩余寿命预测[J].电源技术,2018,42(10):1438-1440.
[11] JUNIOR J R B,NICOLETTI M C,ZHAO L.An embedded imputation method via attribute-based decision graphs[J].Expert Systems with Applications,2016,57(5):159-177.
[12] 戴震宇,刘志茹.基于容量和电压的混合最优控制均衡[J].电子技术应用,2019,45(3):108-112.
[13] BEQUAO A,LESSMANN S.Extreme learning machines for credit scoring: An empirical evaluation[J].Expert Systems with Applications,2017,86(7):42-53.
[14] SOVILJ D,EIROLA E,MICHE Y,et al.Extreme learning machine for missing data using multiple imputation[J].Neuro-computing,2016,174(A):220-231.
[15] SBARUFATTI C,CORBETTA M,GIGLIO M,et al.Adaptive prognosis of lithium-ion batteries based on the combination of particle filters and radial basis function neural networks[J].Journal of Power Sources,2017,344:128-140.
作者信息:
汪秋婷,戚 伟
(浙江大学城市学院 信息与电气工程学院,浙江 杭州310015)

