0 引言

    纠错码技术在数字通信中具有重要作用，其中卷积码的编码方式，由于优良的纠错性能被广泛应用，而Viterbi译码方式作为卷积码的一种最佳概率译码方法，对于卷积码的广泛应用具有重要价值^[1-2]。近年来，FPGA作为一种半定制电路，广泛应用于数字信号处理系统中，为Viterbi译码器的实现提供了有利条件^[3]。

    评价Viterbi译码器性能的指标主要是译码速度和资源消耗，因此如何减小译码时延、提高译码速度、降低资源消耗成为近年来研究的热点^[4]。文献[5-6]通过改进文献[7-8]网格图的构造来降低译码时延、提高译码速率，文献[5]采用基二算法，文献[6]采用基四算法。其中基二算法的资源消耗小，但基二算法的数据处理能力比基四算法弱；基四算法处理数据能力比基二算法强，但基四算法的主频低，速度难以提升。文献[9-10]通过改进Viterbi的迭代方式提高译码速度，但是该方法复杂度高，资源消耗大。文献[11]通过改进回溯结构来降低译码时延、提高译码速率，在文献[6]的基础上提出了基于滑窗流水的前向回溯基四算法，但该方法添加了冗余滑窗，资源消耗大，不适用于资源有限的场景。

    为了使Viterbi译码算法可以在XC6SLX16-2CSG-324型FPGA上实现，并针对目前大多数改进算法在资源有限条件下难以兼顾时延与资源消耗，本文在基二算法的基础上提出了一种改进算法。该算法在基二算法的基础上，对Viterbi译码器的度量控制和幸存路径信息存储模块分别进行了改进，提高基二算法的数据处理能力，在资源有限条件下，能够有效简化译码器的实现结构，进而兼顾时延与资源消耗，提高译码性能。

1 改进Viterbi算法

1.1 算法原理

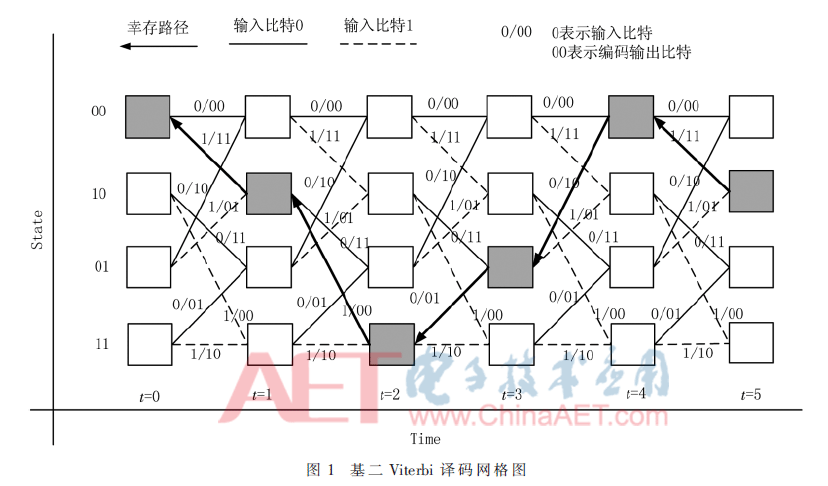
    Viterbi算法是一种用于解决有限状态离散时间马尔科夫链的状态估计问题的优化算法^[12]。图1^[1]所示的基二网格图显示了卷积码的译码过程，具体描述可参见文献[1]。时间节点t表示第t个信息码元，Viterbi译码器从网格中找出最大似然路径。

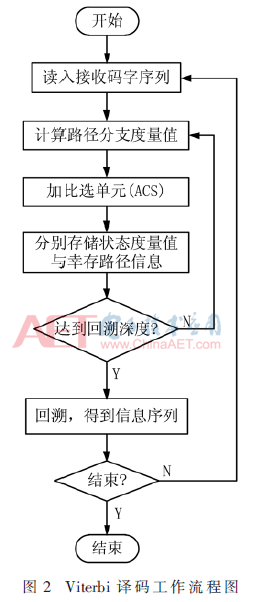
    Viterbi译码器的工作流程如图2^[3]所示。将接收机^[13]每一时刻从信道接收到的信息序列与编码网格中所有的信息序列进行比较，根据软判决原理计算各分支路径度量值，并与该分支下一时刻进入状态的度量值进行累加，保留进入每个状态的度量值最小的分支路径和幸存路径信息，当达到回溯深度时，选出度量值最小的状态作为开始逆向回溯的初始状态，根据幸存路径信息找到回溯的最大似然路径。

    记(n₀，k₀，m)为卷积码编码器，该编码器共有2k₀×m个状态，Viterbi译码器必须具备同样的2k₀×m个状态发生器，且每个状态必须有一个存储路径度量值的存储器和一个存储幸存路径信息的存储器，所以Viterbi译码器的复杂度呈2k₀×m指数增长^[1]。

1.2 算法改进的具体描述

    基二Viterbi译码器主要由分支度量计算单元(BMU)、加比选单元(ACSU)、路径度量存储单元(PMU)、幸存路径存储单元(SMU)、回溯单元(TBU)构成，系统框图如图3^[3]所示。

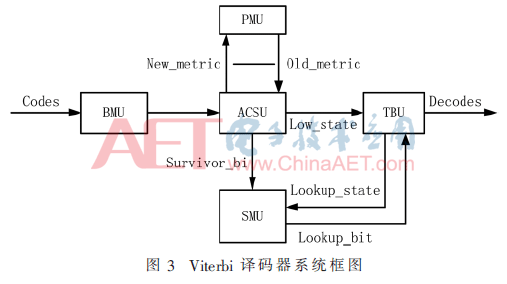
    改进算法在基二算法的基础上，主要对ACSU中度量控制结构和SMU的存储结构进行改进。记S_i为状态i，PMi为状态Si的路径度量累加值，τ为回溯深度(τ=L+m，L为信息码元数)，Sub_bit为幸存路径信息，算法改进的具体描述如下：

2 理论分析

2.1 离散无记忆信道(DMC)模型

    Viterbi译码算法的性能可由译码器输出的误码率进行分析。由于改进算法采用软判决，这里主要针对高斯白噪声(AWGN)下，BPSK调制的DMC信道模型根据不同回溯深度τ，τ=(5～10)m做误码率分析。DMC信道模型如图5^[1]所示，q为电平量化序列，左边表示信道输入为二进制0、1，右边表示信道输出为0～(q-1)，p(q-1|0)表示输入为0输出为q-1的概率^[1]。

    根据信道编码定理，二进制对称信道(BSC)下，对某一给定的(n₀，k₀，m)卷积码，采用最大似然译码的Viterbi译码器产生错误事件的概率P_E为^[1]：

2.2 改进算法分析

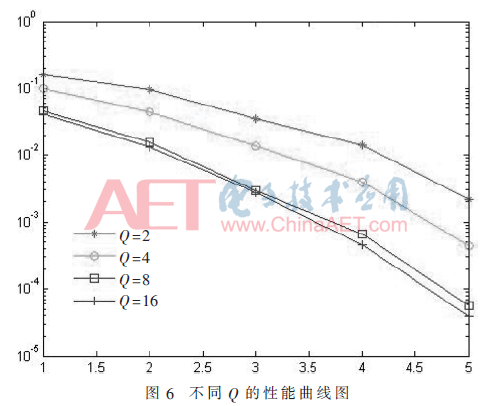
    给定(2，1，4)卷积码，对于Viterbi的截尾译码器，回溯深度τ满足τ=(5～10)m即可^[1]，为节约度量寄存器资源，本文选择τ=20。然后在τ=20的情况下改变Q值，如图6所示。可以看出Q<8时判决增益增加比较明显，当Q>8后判决增益增加很慢。因此实际应用中一般选用八电平和十六电平量化，译码器不会太复杂，且有2~3 dB软判决增益^[1]。因此选择τ=20，Q=8能有效保证译码器性能。

3 仿真分析

3.1 MATLAB仿真结果分析

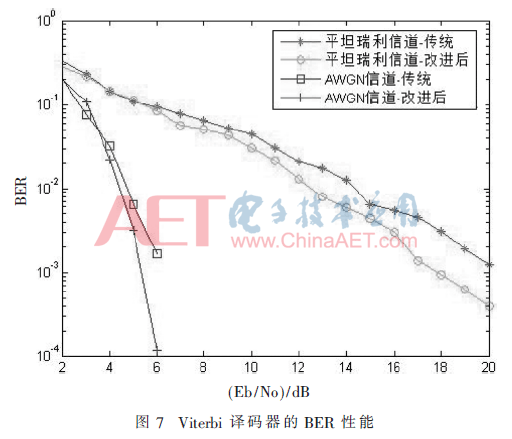
    在MATLAB中，对Viterbi译码器分别在AWGN信道和平坦瑞利衰落信道中译码进行建模，给定(2，1，4)卷积码，当τ=20，Q=8时，对传统和改进后的译码器分别在AWGN信道和平坦瑞利衰落信道中进行仿真。该模型中，输入信道的信号为二进制相移键控(Binary Phase Shift Keying，BPSK)调制信号，信道的输出量化成八进制。误比特率(Bit Error Rate，BER)统计性能如图7所示。从BER性能来看，在AWGN信道中本文采用的Viterbi算法与传统的Viterbi算法相比，增益提高了约0.5 dB；在平坦瑞利衰落信道中本文采用的Viterbi算法与传统的Viterbi算法性能相比，在低信噪比时增益提高不明显，在高信噪比时增益提高了约1 dB。

3.2 ISE仿真结果分析

    针对τ=20，Q=8的(2，1，4)译码器，本文基于Verilog硬件描述语言对各模块进行了RTL级描述，并用ISE Design Suite 14.7进行了功能仿真。

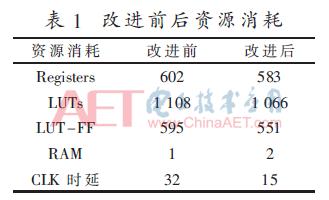
    对改进前与改进后的Viterbi译码器进行ISE仿真，资源消耗与时延如表1所示。表中可以看出，采用本文提出的度量控制方法和幸存路径存储结构的Viterbi译码器达到回溯深度后只需15个CLK延迟便可以译出第一个码元，采用传统的度量控制与RE幸存路径存储结构的Viterbi译码器需要32个CLK延迟。改进后的译码器在速度上有了很大的提高，同时资源消耗也有了一定的节约。

    Viterbi译码器的测试主要包括功能验证与译码器的纠错性能两部分。

    首先进行功能验证，所有数据都是理想的。因为τ=20，则译码器以20个数据为一组译码，本文的Viterbi译码器采用的是截尾译码，故利用MATLAB产生16个随机序列加上4个0组成一组信息序列为C1：11111101101110110000，经过编码器后的输出序列为C2：11_10_11_01_10_10_01_11_11_11_00_11_00_10_11_11_11_11_01_11，八电平量化后的序列为C3：111111_111000_111111_000111_111000_111000_000111_111111_111111_111111_000000_111111_000000_111000_111111_111111_111111_111111_000111_111111，将C3序列作为Viterbi译码器的输入，ISE仿真结果如图8所示。

    图中Clk为码元时钟，code是C3序列，TB_flag为1表示达到回溯深度，code_in为译码输出结果：11111101101110110000，与C1序列完全相同，故此译码器功能正确。

    其次是纠错性能测试，在理想数据中人为加入错误的干扰信息。经计算，(2，1，4)译码器的d_f=7，故理论上此译码器可在5段连续译码中纠正3个随机错误。经测试，在20个连续码元段中加入3个随机错误码元，即误比特率为2.5%的情况下，译码器可以将错误完全纠正。在20个连续码元段中加入4个随机错误码元，即误比特率为3.33%时不能将错误完全纠正，但若错误码元之间间隔≥5段码元时也可完全纠正。理论值的纠错性能是在译码深度无限长时计算出来的，而无限长的译码深度在硬件上是无法实现的，因此在实际应用中的纠错性能会与理论值有一定的差距，但在实际通信系统中，调制后通过信道传输的错误码率远未达到10^-2这个数量级^[1]。如图7所示，在AWGN信道中，只要信噪比大于4.5 dB，误码率就小于10^-2这个数量级；在平坦瑞利衰落信道中，只要信噪比大于14 dB，误码率就小于10-2这个数量级，而实际通信系统中信道的信噪比远远大于14 dB，因此本文改进的Viterbi译码器能够满足实际应用中的需求^[1]。

4 结论

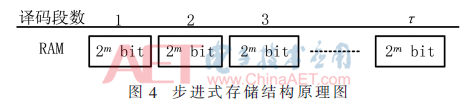
    本设计主要针对ACS和SMU单元，简化译码器的结构，降低硬件实现的复杂度，提高运算速度。在加比选单元的控制度量部分，为了解决路径度量数据溢出问题，本文提出了预定义存储度量值寄存器容量法，减小了运算量，提高了译码速度。在幸存路径存储部分，优化了存储方式， 采用步进式存储方法，降低了译码器的功耗。回溯译码时，采用奇偶回溯法译码方式，根据幸存状态的奇偶性完成输出，减小了RAM的存储空间。仿真结果表明，本文的优化设计能够大大简化硬件电路的结构，在译码器的设计中具有应用价值。

参考文献

[1] 王新梅，肖国镇.纠错码—原理与方法(修订版)[M].西安：西安电子科技大学出版社，2001.

[2] GAO Z，ZHU J，HAN R，et al.Design and implementation of configuration memory SEU-Tolerant Viterbi decoders in SRAM-based FPGAs[J].IEEE Transactions on Nanotechnology，2019，18：691-699.

[3] 张慎.卷积码编码器及Viterbi译码器的设计[D].成都：电子科技大学，2008.

[4] 平磊.面向5G通信的咬尾卷积码和Turbo码技术研究[D].西安：西安电子科技大学，2017.

[5] MAMARDE R，KHOJE S.Viterbi decoder using Zynq-7000 AP-SoC[C].2018 Second International Conference on Intelligent Computing and Control Systems(ICICCS).IEEE，2018：941-944.

[6] EL-GOHARY A，SAAD M，MAHMOUD O，et al.Low utilization FPGA implementation of OFDM transceiver based on IEEE 802.11 n standard[C].2019 8th International Conference on Modern Circuits and Systems Technologies(MOCAST).IEEE，2019：1-4.

[7] ZHOU L，TANG M，LIU D，et al.A flexible viterbi decoder for software defined radio[J].Journal of Theoretical and Applied Information Technology，2013，47(2)：702-706.

[8] SANTHI M，LAKSHMINARAYANAN G，SUNDARAM R，et al.Synchronous pipelined two-stage radix-4 200Mbps MB-OFDM UWB Viterbi decoder on FPGA[C].2009 International SoC Design Conference(ISOCC).IEEE，2009：468-471.

[9] 朱明哲，肖瑞，苏小凡，等.混合噪声下基于Viterbi同步压缩S变换的FM信号分析[J].电子与信息学报，2018，40(12)：2913-2918.

[10] YOSHIKAWA H.Error performance analysis of the K-best viterbi decoding algorithm[C].2018 International Symposium on Information Theory and Its Applications(ISITA).IEEE，2018：257-260.

[11] AHMED S，SIDDIQUE F，WAQAS M，et al.Viterbi algorithm performance analysis for different constraint length[C].2019 16th International Bhurban Conference on Applied Sciences and Technology(IBCAST).IEEE，2019：930-932.

[12] 杨敏.高速率低延时Viterbi译码器的设计与实现[J].电子技术应用，2018，44(9)：56-58，62.

[13] 辛渊博，侯宏.基于FPGA的数字信道化接收机的研究及实现[J].电子技术应用，2009，35(5)：163-165，170.

[14] 仇佩亮，陈惠芳，谢磊.数字通信基础[M].北京：电子工业出版社，2007.

作者信息:

吴雪玲，江  虹

(西南科技大学 信息工程学院，四川 绵阳621000)