近乎完美的DDS正弦波信号音生成器
2020-08-25
作者:Patrick Butler,现场应用工程师
来源:ADI
在测试和验证分辨率高于16位的高精度快速模数转换器(ADC)的交流性能时,需要用到近乎完美的正弦波生成器,该生成器至少支持0 kHz至20 kHz音频带宽。通常会使用价格高昂的实验室仪器仪表来执行这些评估和特性表征,例如Audio Precision提供的音频分析仪AP27xx或APx5xx系列。大多数情况下,24位或更高分辨率的现代高速SAR和宽带Σ-Δ ADC都采用单电源和全差分输入,因此要求用于DUT的信号源具备准确的直流和交流性能,同时提供全差分输出(180°错相)。同样,这款交流生成器的噪声和失真水平应该远优于这些ADC的规格,根据大部分供应商提供的规格,其本底噪声水平远低于 -140 dBc,失真水平低于-120 dBc,输入信号音频率为1 kHz或2 kHz,最高可达20 kHz。有关适合高分辨率带宽ADC的典型测试台的典型测试配置,请参考图1。最关键的元件就是正弦波生成器(单信号音或多信号音),其中基于软件的直接数字频率合成器(DDS)可以提供完全的灵活性、极高的频率分辨率和时钟同步性能,利用数据采集系统来执行相干取样,以避免泄漏和FFT窗口滤波。
因为成本只有音频精密分析仪的几分之一,所以能够基于直接数字频率合成(DDFS)原理设计非常精准的正弦波生成器,但需要通过软件在SHARC处理器等浮点DSP处理器上实现。一个相当快的浮点DSP将能满足实时性要求,以及所有算法和处理条件,以达到先进的SAR ADC所设置的失真和噪声性能水平。通过利用SHARC内核架构的全字数据长度(32位或64位定点格式)来实施NCO相位累加,利用专有的40位浮点扩展精度来执行正弦近似函数,以及利用数字滤波器来确定频谱形状,量化效应(回转噪声和截断噪声)得到大幅降低,与用于信号重构的数模转换器(DAC)缺点相比,这种效应可以忽略不计。
直接数字频率合成
1970年4月,Joseph A. Webb1提出了数字信号生成器频率合成器的专利申请,其中描述了有关DDS生成包括正弦波等各种模拟波形的考虑因素,只需使用数个数字逻辑模块即可实现。之后,Tierney等人2在1971年初发表了论文(后来成为大家频繁引用的参考文献),阐述了通过深化DDS操作进行正交生成来实现直接数字频率生成,以及采样系统理论相关局限性(字词截断和频率规划)问题。随后出现的实际应用大部分依赖于分立式标准逻辑IC,例如TTL 74xx或ECL 10K系列。后来在不到10年的时间里,Stanford Telecom、Qualcomm、Plessey和ADI等纷纷推出了完全集成式解决方案,例如ADI的AD9950和AD9955。这些逻辑IC旨在实现速度、功率和成本之间的最佳平衡,其架构基于查找表(LUT),以确保在有限相位、频率和幅度分辨率下实现相位-正弦幅度转换。如今,ADI公司仍然是DDS独立集成电路的最大供应商,可能也是最独特的供应商,而当前的数控振荡器(NCO)往往都集成到AD9164 或AD9174 之类RF DAC中。虽然这些器件在多GHz带宽上具备出色的噪声和线性度性能,但它们都不适合测试中等速度、高分辨率ADC,例如LTC2378-20 、AD4020 或AD7768 。
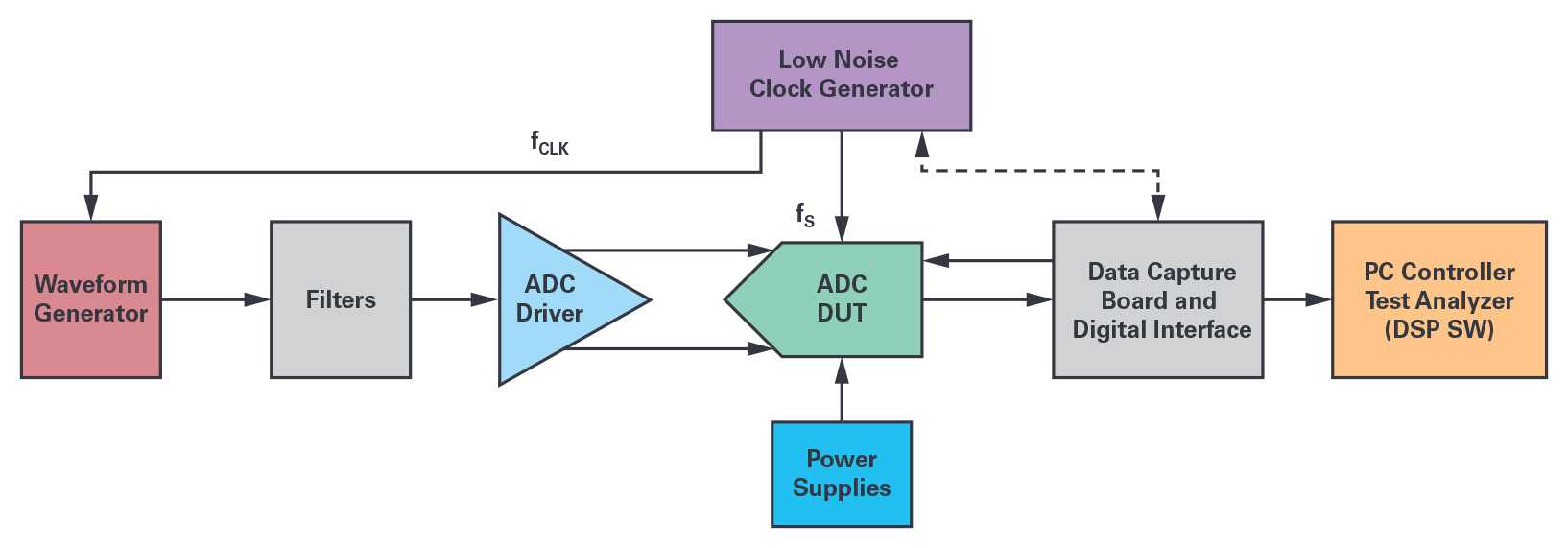
图1.基于IEEE 1241标准的典型ADC(ac)测试设置的处理链。DDFS能够让整个测量系统完全实现数字化,具备多种优势,包括完全的灵活性和相干取样采集
与基于PLL的传统频率合成器相比,NCO和DDS的显著优势包括:极高的频率分辨率、快速灵敏性,以及可轻松生成完美正交的正弦/余弦波形。此外,还提供宽带宽范围和高直流精度。其工作原理受数字信号处理和采样系统理论,数字特性支持对输出信号的相位、频率和幅度实施全数字独立控制。图2所示的框图显示传统DDS的架构,该DDS由三大功能模块组成:
·N位相位累加器;
·相位-正弦幅度转换器,由W位截取相位输入字表征特性;
·D位DAC及其相关重构滤波器。
相位累加器由简单的N位加法器结合寄存器构成,寄存器的内容按照采样时钟FCLK的速率,以输入相位增量Δθ(通常也称为频率调谐字,FTW)更新。累加器会定期溢出,在采样或参考时钟FCLK和DDS输出频率FOUT之间像小数分频器一样运行,或像齿轮箱一样运行,分频比为:

溢出速率为生成的波形提供输出频率,使得:

其中0 ≤ FTW ≤ 2N-1。因为分频器的原因,NCO输出端的参考或采样fS时钟相位噪声的影响会降低
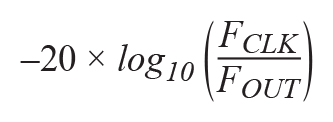
相位累加器寄存器的输出表示生成波形的电流相位。每个分立式累加器输出相位值然后通过相位-正弦或相位-余弦映射引擎,被转换成幅度正弦或余弦数据或样本。此功能通常利用存储在LUT(ROM)中的三角函数值完成,有时通过执行正弦近似算法完成,或两者组合方式完成。相位-正弦幅度转换器的输出供DAC使用,在滤波之前生成量化和采样正弦信号,使信号平稳,并避免频谱混叠。由DAC有限分辨率导致的幅度量化设定了本底噪声以及相应的频率合成器信噪比(SNR)的理论限值。此外,DAC作为混合信号器件,由于其INL、DNL、压摆率、毛刺和建立时间等特性,展现出一系列直流和交流非线性,这会产生杂散信号音,缩小正弦波生成器的整个动态范围。
基于图2中架构实现的实际正弦波形生成器,主要是相位-幅度转换模块不同,受数字无线电应用这一市场导向影响,该模块通常针对速度和功耗,而不是高精度而优化。实施相位-正弦幅度转换器最简单的方法就是使用ROM,采用一对一映射的方式来存储正弦值。遗憾的是,LUT的长度与相位累加器的宽度N呈指数增长(2N),并且与波表数据字精度W呈线性增长。而且,减小累加器的尺寸或截断其输出之间的权衡和取舍会导致频率分辨率降低,并且严重降低SFDR的性能。结果表明,相位或幅度量化导致的杂散会降低-6 dB/位。实现精细的频率调谐通常需要较大的N,已有几种技术可用来限制ROM的尺寸,同时保持足够的杂散性能。一般会使用简单的压缩方法,利用正弦或余弦函数的四分之一波长对称性将相位幅度范围减小4倍。为了进一步缩小范围,实际会使用截断相位累加器输出的方法,不过这会导致产生杂散谐波。尽管如此,这种方法也因精准的频率分辨率要求、存储器尺寸和成本考量而得到了广泛采用。建议采用多种角分解方法,以降低基于LUT的方法对存储器的要求。与使用各种分段、线性或多项式内插法的幅度压缩结合,在进行需要正弦和余弦函数的I/Q合成时,准确估算正弦函数的第一象限,或按[0, π/4]间隔估算。同样,在没有ROM LUT的情况下,只需要按照逐次逼近的方法调用位移和添加操作,即可使用基于角旋转的方法有效生成复杂信号。这种方法以流行的CORDIC为代表,当硬件乘法器不可用时,或者出于速度或成本考虑,应最大限度减少实施函数所需的栅级数量时(在FPGA或ASIC中),此方法通常比其他方法更快。相反,当硬件乘法器可用时(在DSP微处理器中总是如此),采用插入方法和完整多项式计算(例如泰勒级数展开、切比雪夫多项式)的表查找要比CORDIC更快,尤其是要求高精度时。

图2.NCO的主要功能部分,以及与完整的直接数字频率合成器的区别,其中包括重构DAC和其相关的AAF。NCO部分可用于测试或仿真DAC
在软件中实现高精度NCO
如同著名的惠普分析仪,或者如同应用笔记AN-1323中描述的那样,构建与最出色的模拟振荡器具备同等或更出色的失真性能的高精度交流信号振荡器并不容易,即使是针对音频频谱(直流至20 kHz范围)。然而,如前所述,利用嵌入式处理器具有的足够运算精度来执行相位计算(ωt)和正弦函数(sin(ωt))近似计算,从而完整实施软件,这显然有助于最大限度减少量化的不利影响、噪声和由此导致的杂散。这意味着图2中的所有NCO功能模块都会转换成代码行(不是VHDL!),从而实现一个满足实时约束的软件版本,以确保实现最小的采样速率和所需的频率带宽。
对于相位-正弦幅度转换引擎,完整的LUT方案或任何变化都需要用到太多的存储空间或太多的插值运算来实现完美的正弦一致性。相反,用于计算正弦近似值的多项式方法允许使用成本极低的通用DSP,在复杂性与精度之间达成了不错的平衡。多项式级数展开也很有吸引力,因为它相对简单,并且能够采用选择的幂级数类型提供充分的灵活性,并且调整算法来实现给定精度。它不需要很大的存储空间(可能不到100行SHARC DSP汇编代码),只需要几个RAM位置来存储多项式系数和变量,因为正弦值只在采样时刻计算。
首先,对于正弦近似值函数,显然会选择使用具有适当顺序的泰勒/麦克劳林幂级数来满足目标精度。但是,由于幂级数在端点处往往会失效,所以在执行任何多项式求值之前,必须将参数输入范围缩小到更小的区间。如果不缩小参数范围,只能使用非常高阶的多项式来支持在功能域(例如[-π, +π])中实现高精度。所以,需要对初等函数进行一些变换,以获取所需的约化参数,例如sin(|x|) = sin(f + k × π/2)和sin(f) = sin(x - k × π/2),其中0 ≤f<π/2。因此,对于三角函数,要特别注意不要使用减法相消,以免严重降低精度,并导致灾难性后果,特别是在运算精度极差的情况下。在我们的例子中,当相位输入大于或接近π/2的整数倍数时,会发生这种情况。
除了周期性和modulo-2π重复之外,sin(x)函数的对称性可用于进一步缩小近似值范围。鉴于正弦函数在区间[0, 2π]内,关于点x = π不对称,所以能够使用以下关系式:
sin(x+π)+-sin(x)
将范围缩小到[0, π]。采用同样的方式,sin(x)在区间[0, π]内,关于由x = π/2定义的线对称,所以:
sin(x+π/2)+sin(π/2-x)
x在区间[0, π/2]以内,这会进一步缩小角输入近似值的范围。通过进一步缩小参数区间(例如[0, π/4])来提高精度并不是有效方法,因为这需要同时估算正弦和余弦函数的值,如常用三角关系所示:sin(a+b) = sin(a) × cos(b) + cos(a) × sin(b),从生成正交信号这一角度,这有其价值。
ADI公司的ADSP-21000系列应用手册第1卷描述了一个近乎理想的(用于嵌入式系统)正弦近似值函数,该函数基于为第一个ADI DSP浮点处理器编写的幂级数优化,即ADSP-21020,后者基本上属于SHARC核。这种sin(x)的实现方法依赖于Hart等人4发布、由Cody和Waite5完善、适用于浮点运算的极大极小逼近多项式,以减少舍入错误和避免出现前面提到的取消。极大极小方法依赖于切比雪夫多项式和雷米兹交换算法来确定所需的最大相对误差的系数。如图3中的MATLAB?所示,与第七阶泰勒多项式6相比,设置系数的微小变化可能会明显提高极小极大值的精度。为了实现精度与速度的最佳平衡,这个正弦近似值函数的角输入范围应该缩小到[-π/2至+π/2]区间内,且软件程序包含一个有效的范围缩减滤波器,约占总“正弦”子程序执行时间的30%。
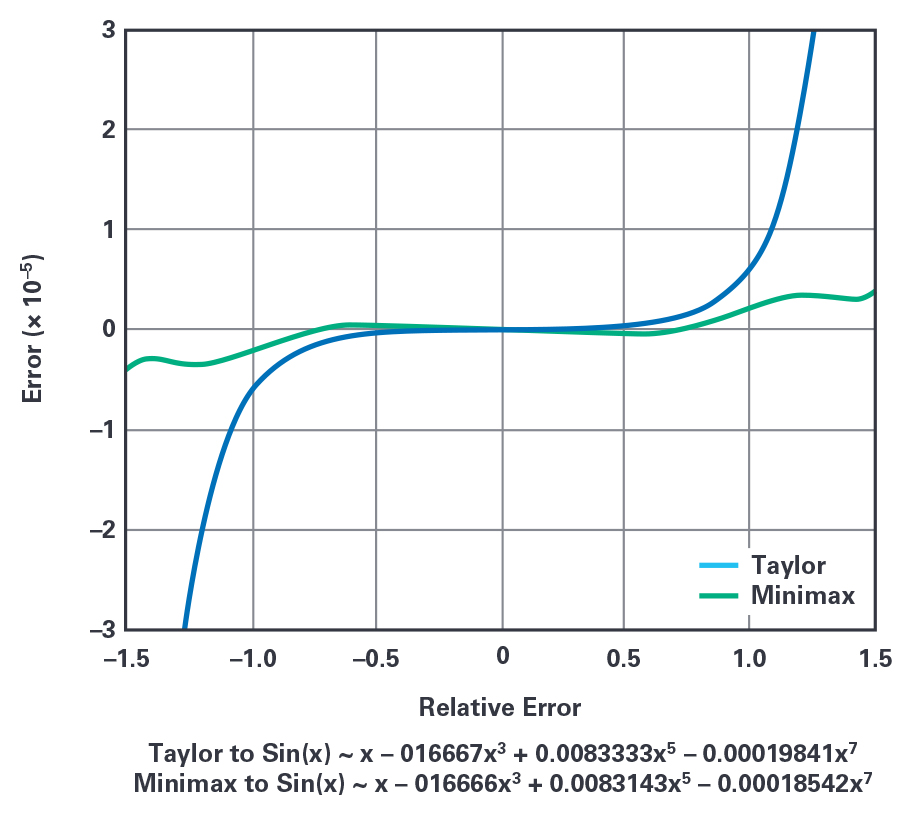
图3.不同于泰勒-麦克劳林方法围绕0进行定义,极小极大正弦逼近方法在[-π/2至+π/2]区间内,会最小化和均衡最大相对误差。
虽然所有计算都可以使用32位定点算法执行,但多年以来,最常见和最方便的数学计算格式是IEEE 754浮点标准,特别是在处理长数字时。作为一家DSP VLSI芯片制造商,ADI公司从一开始就率先采用了IEEE 754-1985标准。当时还没有单芯片浮点DSP处理器,只有简单的浮点乘法器和ALU计算IC,如ADSP-3212和ADSP-3222。这种格式取代了计算机行业的大多数专有格式,成为所有SHARC DSP处理器的本机格式,采用单精度32位、扩展精度40位,以及最近出现的适用于ADSP-SC589 和ADSP-SC573 的双重精度64位。
具备32位尾数的SHARC 40位扩展单精度浮点格式为这种正弦波生成应用提供了足够的精度(u 2-32),且有助于保持均等,Cody和Waite表示第15阶多项式的总体近似精度为32位,在[0至+π/2]输入域内具有均匀分布的误差。为了最大限度减少运算次数并保持精度,最后的调整是对多项式计算执行霍纳法则,这是一种快速求幂的方法,可以求取一个点的多项式值,所以:

R1至R7是多项式级数的Cody和Waite系数,只需要进行8次乘法和7次加法即可计算任何输入参数ε[0, π/2]的正弦函数值。以汇编子程序的形式编写的完整sin(x)近似代码在SHARC处理器上大约执行22个核心周期。原有的汇编子程序在更改之后,在获取40位多项式浮点系数时执行同步双存储器访问,以减少6个周期。

图4.软件DDS简化框图给出了处理单元之间的各种量化步骤的数据运算格式和位置。
NCO 64位相位累加器本身在执行时,就用到了双精度2的小数格式的SHARC 32位ALU。提供存储器更新的整个相位累加器执行过程需要11个核心周期,因此,每个NCO输出样本都在约33个核心周期内生成。
图4中的框图显示了基于软件DSP的NCO的功能模块实现方案,每级都参考了运算格式精度。此外,进行信号模拟重构以及实现完整的DDFS还需要用到一个或两个DAC及其模拟抗混叠滤波器电路。处理链的关键元件包括:
·64位相位累加器(SHARC ALU双精度,带溢出);
·64位小数定点到40位浮点转换模块;
·范围缩减模块[0至+ π/2]和象限选择(Cody和Waite);
·正弦逼近算法(Hart),用于相位-幅度转换;
·-1.0至+1.0范围内的sin(x)重构和归一化级;
·LP FIR滤波器和sin(x)/x补偿(如果必要);
·以及40位浮点至D位定点转换和标度函数,以匹配DAC数字输入。
可以在NCO输出端放置一个可选的数字低通滤波器,以去除可能进入目标频段的杂散和噪声。或者,该滤波器可以提供插值和/或逆sin(x)/x频率响应补偿,具体由选择用于模拟重构的DAC决定。这种低通FIR滤波器可以使用MATLAB Filter Designer工具设计。例如,假设采样频率为48 kSPS,带宽为DC至20 kHz,带内纹波为0.0001 dB,带外衰减为-150 dB,则可以实施具有40位浮点系数的高质量均衡纹波滤波器。它只有99个滤波系数,在单指令单数据(SISD)单计算单元模式下,总执行时间将消耗约120个SHARC核心周期。经过数字滤波后,使用其中一个DSP同步串行端口,由DMA将计算的样本对发送至DAC。为了获得更好的速度性能,链接DMA操作也可以使用大型乒乓存储器缓冲区来支持块处理操作。例如,块数据大小可以等于FIR数据延迟线的长度。
为了实现最佳SFDR,在NCO上进行的最后调整
如前所述,NCO遭受杂散的主要原因是对相位累加器输出的截断,其次是针对通过计算或列表得出的正弦值的幅度量化。相位截断引起的误差通过相位调制(锯齿形)在载波频率附近产生杂散,而正弦幅度量化引起与谐波相关的杂散,不过长期以来一直被认为是随机误差和噪声。如今,在Henry T. Nicholas和H. Samueli撰写的技术论文7中,从数学角度深入阐述了相位累加器的操作。在深入分析的基础上,提出了一种模型,将相位累加器视为分立式相位样本排列生成器,并据此预测频率杂散。无论相位累加器参数(M、N、W)是多少,相序的长度都等于
(其中GCD是最大公约数),如图4所示,由频率调谐字M最右边的位位置L决定。因此,L的值定义序列类别,这些类别彼此共享自己的相位分量集,但根据
比率重新排序。这些在时域内生成的截断相位样本序列被用来通过DFT确定频率域内各杂散线各自的位置和大小。这些序列还表明,M (FTW)的奇数值显示最低频率杂散的幅度,并建议对相位累加器进行简单的修改以满足这些最低程度的条件(只需在FTW中添加1 LSB)。如此,相位累加器的输出序列必须始终具有相同的2N个相位元素,无论相位累加器的M值和初始内容是什么。之后,最差的杂散信号音幅度等级降低3.922 dB,等于SFDR_min (dBc) = 6.02 × W。由Nicholas更改的相位累加器为NCO提供了多种优势,首先,它消除了FTW最右边的位非常接近MSB(FMCW应用中的频率扫描)的情况,其次,它让杂散幅度与频率调谐字M无关。这种修改可以通过按采样速率fS切换ALU LSB来轻松实现,如果FTW LSB置位至逻辑1,则可以仿真与相位累加器相同的行为。相位累加器大小N = 64位时,对于所需频率FOUT的精度,可以将? LSB偏移视为可忽略的误差。
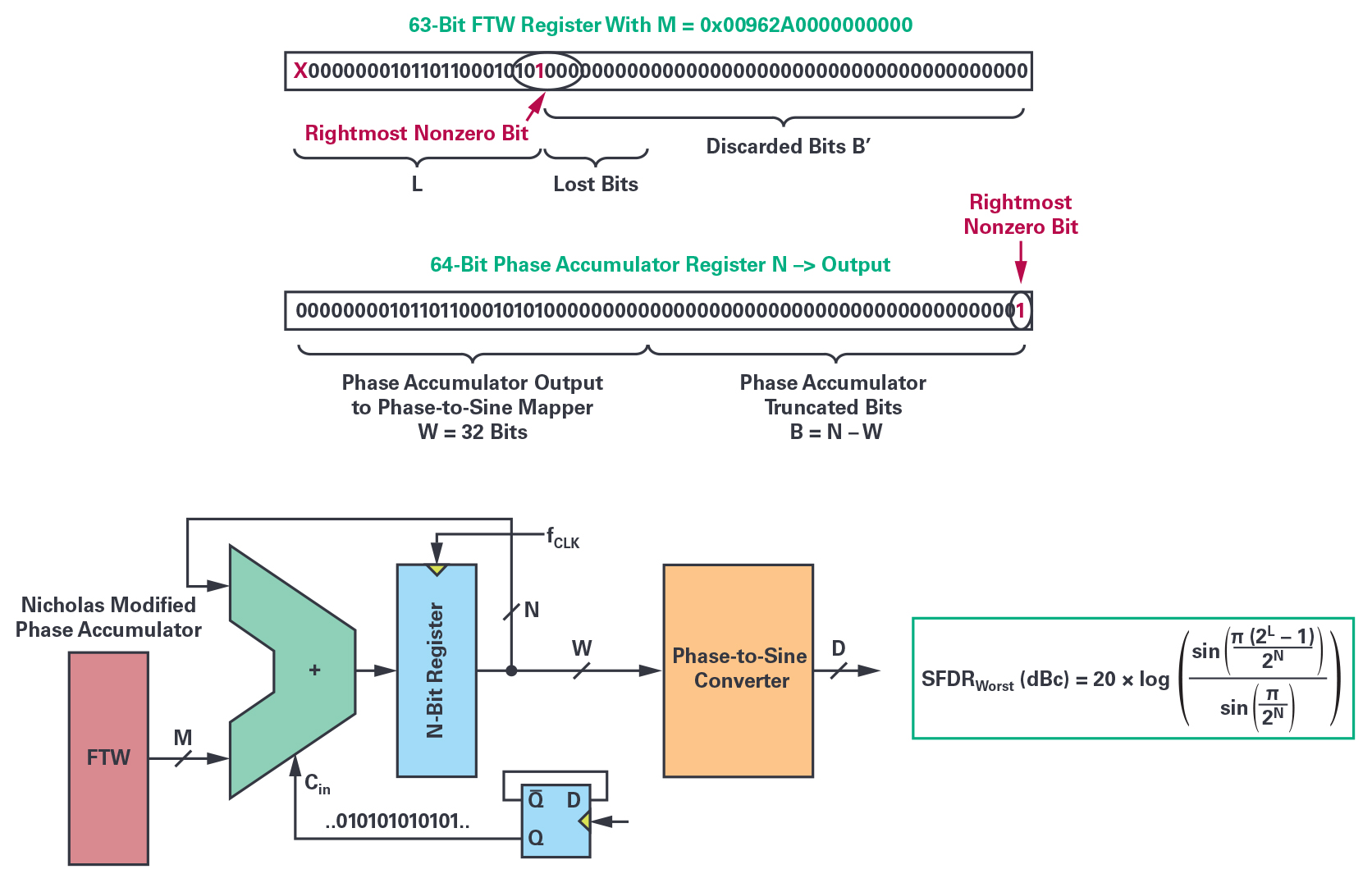
图5.FTW最右边非零位的位置确定了理论上SFDR的最差水平。由Nicholas修改的相位累加器解决了采用任何N值的问题,并且使NCO的SFDR最大。
采用32位输出相位字W时,由相位截断导致的最大杂散幅度会限制为-192 dBc!正弦采样值的有限量化也会导致产生另一组频率杂散,该杂散通常被认为是噪声,可采用大家熟知的SNRq(dB) = 6.02 × D + 1.76公式进行估算。这必须添加到寄生参数中,因为相位-正弦幅度转换算法阶段的近似误差被认为是可以忽略的,但是,必须非常谨慎地选择相位-正弦近似算法和计算精度。
这些结果表明,从理论水平上,我们的软件正弦NCO的线性和噪声都远远超过了测试市场上大多数高精度ADC所需的阈值。它仍然需要找到信号链中最后一个、也是最关键的元件:重构DAC及其互补模拟抗混叠滤波器和相关的驱动电路,以满足预期的性能水平要求。
重构DAC:关键之处!
首先可能会选择具备出色的非线性误差(INL和DNL)规格的高精度DAC,例如出色的20位高精度DACAD5791 。但是它的分辨率只有20位,而且其R-2R结构不支持实施信号重构,特别是产生非常纯的正弦曲线,这是因为在输入代码转换期间,它存在很大毛刺。传统的DAC架构基于二进制加权电流发生器或电阻网络构建,对数字直通和数字开关损伤(例如外部或内部时序摆动),以及数字输入位的其他开关不对称非常敏感,特别是在会导致能量变化的重大转变期间。这就产生了与代码相关的瞬态,从而产生高幅度谐波杂散。
在20位以上的分辨率下,使用外部超线性快速采样和保持放大器对DAC输出去毛刺并无太大帮助,这是因为它在几十LSB下会生成自己的瞬态,且会因为重采样产生组延迟非线性。信号重构主要存在于通信应用,通过使用分段架构(混合适用于MSB的完全解码部分和适用于最低有效位的二进制加权元件)来解决毛刺问题。遗憾的是,目前还没有超过16位精度的商用DAC。与NCO完全可预测的行为不同,DAC误差难以预测和准确仿真,尤其是当制造商的动态规格很小或者不存在时,但专用于音频应用的DAC或ADC除外。插值过采样和多位∑- DAC似乎是唯一的解决方案。这些先进的转换器具有高达32位的分辨率、超低失真和高信噪比,是在中低带宽内实施信号重构的最佳选择。为了在音频频谱或稍宽的频段(20 kHz或40 kHz带宽)内实现出色的噪声和失真性能,可以使用ADI公司产品系列中杰出的∑-? DAC产品,音频立体声DACAD1955 , 虽然分辨率最高为24位,这款DAC仍然是市场上非常受欢迎的音频DAC。
这款音频DAC于2004年推出,基于多位Σ-Δ调制器和过采样技术,配合各种技巧,用于缓解这种转换本身固有的失真和其他问题。
即使目前,AD1955采用的插值LP FIR滤波器仍然是同类出色产品。它具有极高的阻带衰减(≈-120 dB)和极低的带内波纹(≈±0.0001 dB)。它的两个(左侧和右侧通道)DAC可以以最高200 kSPS速度运行,但在48 kSPS和96 kSPS时实现最佳交流性能,其动态范围以及立体声模式下的SNR,都支持典型的EIAJ标准、A加权120 dB系数。在单声道模式下,两个通道同时异相组合,性能有望提高3 dB。但是,对于宽带应用,这些规格不太实际,这是因为它们是合成的,带宽范围在20 Hz至20 kHz之间。带外噪声和杂散不会超过20 kHz,部分是因为EIAJ标准、A加权滤波器和音频行业规格定义。这种满足特定音频测量要求的带通滤波器模拟人耳的频率响应,与未滤波的测量值相比,性能提高3 dB。
DDFS硬件演示平台:采用AD1955实现正弦波重构
整套DDFS使用两个评估板实现,一个支持DSP处理器,一个适用于采用AD1955 DAC进行模拟信号重构。选择第2代SHARC ADSP-21161N 评估板的原因在于其可用性、易用性,以及适合任何音频应用的精简配置。目前仍在量产的ADSP-21161N于不久之前设计,支持工业高端消费电子和专业音频应用,提供高达110 Mips和660 MFlops,或220 MMACS/s容量。与最新一代的SHARC处理器相比,ADSP-21161N最大的不同在于它采用较短的3级指令管道、一个片内1 Mb三端口RAM,以及数量更少的外设。精准信号音生成器的最后和最关键的级基于AD1955评估板,该板必须从软件NCO提供的样本中,以完全还原的方式重构模拟信号。这个评估板带有一个抗混叠滤波器(AAF),优化音频带宽来满足Nyquist标准,除了常用的S/PDIF或AES-EBU接收器外,还配有两个串行音频接口,用于支持PCM/I2S和DSD数字流。PCM/I2S串行链路连接器用于将AD1955 DAC板连接到ADSP-21161N EVB的串行端口1和3连接器(J)。这两个板都可以配置为采用I2S PCM或DSP模式,以48 kSPS、96 kSPS或192 kSPS采样速率运行。DSP串行端口1生成左右通道数据、字选择或左/右帧同步,以及双频DAC的数字输入接口所需的SCK位时钟信号。串行端口3仅用于生成运行DAC内插滤波器和Σ-Δ调制器所需的DAC主时钟MCLK,调制器以比输入采样频率(48 kSPS)快256倍(默认)的速度运行。由于所有DAC时钟信号都由DSP生成,所以使用Crystek提供的超低噪声振荡器CCHD-957替代了板原有的低成本爱普生时钟振荡器。其相位噪声在1 kHz下可能低至-148 dB/Hz,适用于24.576 MHz输出频率。
在模拟输出端,有源I/V转换器必须用于在恒共模电压下(通常为2.8 V)保持AD1955电流差分输出,以最大限度减少失真。像AD797 这样的超低失真和超低噪声的高精度运算放大器能够满足此需求,还可用于处理模拟信号重构。 由于两个差分输出由DSP分别处理,因此选择了具有AAF拓扑结构的立体声输出配置,而不是单声道模式。这个AAF使用LTspice XVII进行仿真,结果如图6所示。由于滤波器的最后一部分是无源的,所以应该像最近推出的ADA4945 那样增加一个有源差分缓冲级。这种具备低噪声、超低失真、快速建立时间特性的全差分放大器是近乎完美的驱动任何高分辨率SAR和Σ-Δ ADC的DAC配件。ADA4945具有相对较大的共模输出电压范围和出色的直流特性,可以提供出色的输出平衡,有助于抑制偶数阶谐波失真产品。
EVB三阶滤波器的-3 dB截止频率为76 kHz,在500 kHz下仅衰减-31 db。这款低通滤波器具备出色的带内平坦性,但带外衰减必须大幅改善,即使是限于纯粹的重构音频应用。要抑制DAC成型噪声和调制器时钟频率MCLK,就必须满足这一点。根据软件DDS的具体使用,用于单信号音生成器或任意波形生成器(生成复杂波形时为AWG),必须优化AAF,以解决带外衰减或群延迟失真。以大家熟悉的SRS DS360超低失真函数生成器为例进行比较,采用7阶Cauer AAF可达到类似的采样速率。信号重构由AD1862完成,后者是一款串行输入20位分段R-2R DAC,适用于数字音频应用。AD1862在高达768 kHz (×16 fS)频率下可以保持20位字采样速率,且具备出色的噪声和线性度。它支持单端电流输出,所以能够使用最出色的放大器来实施外部I-V转换。

图6.LTspice仿真AD1955 EVB三阶抗混叠滤波器(立体声配置)的频率响应。
AD1955和SHARC DSP组合针对多种高分辨率SAR ADC实施测试,例如AD4020 ,其中未设置外部可选无源滤波器。默认情况下,基础AD4020评估板除了板载ADA4807驱动器之外,并无其他选项可用。用于在V_REF/2共模电压下偏置ADC输入的简单电路提供相当低的300 Ω输入阻抗,需要使用信号隔离、交流耦合,或使用外部差分放大器模块,例如EVAL-ADA4945-1。电路笔记CN-0513 中描述的AD4020参考设计板就是一项不错的选择。它包含一个分立式可编程增益仪表放大器(PGIA),提供高输入阻抗,支持±5 V差分输入信号(G = 1)。虽然这些AD4020板和它们的SDP-H1控制器不支持相干采样采集,但它们具备出色的样本波形捕捉长度,最高可达1M。因此,可以实现具备可选窗口的FFT,提供出色的频率分辨率和低本底噪声。例如,对于7项Blackman-Harris窗口,图7中所示的1 Mpts FFT图描述了AD1955在生成的990.059 Hz正弦波下的失真水平。二次谐波是350 kHz带宽内-111.8 dBc下的最大失真分量和最大杂散。但是,在考虑整个806 kHz ADC Nyquist带宽时,SFDR受∑-? DAC调制器、内插滤波器频率和其二次谐波(384 kHz和768 kHz)限制。

图7.从1 M点FFT分析中可以看出,在低于-111 dBc下具备不错的失真性能,在1 kHz输入频率下,10 kHz至200 kHz频段内出现最大杂散。本底噪声约为-146 dBFS。
在相同条件下,对传统的AD1862进行测试,结果显示频率行为略微不同。在差分配置下,两个20位DAC的时钟速度约为500 kSPS,在1.130566 kHz下,本底噪声为-151 dBFS,正弦输出水平为12 V p-p时的THD为-104.5 dB。在AD4020 Nyquist带宽(806 kHz)下,SFDR接近106 dB,受三阶谐波限制。DAC重构滤波器基于两个AD743 <https://www.analog.com/en/products/ad743.html> 低噪声FET放大器,与AD1955评估板中的滤波器一样,属于三阶滤波器,但是-3 dB时的截止频率为35 kHz。
为了变得有效,基于DDS的生成器需要采用不错的滤波器,支持在约250 kHz下实现大于100 dB衰减,以生成达到25 kHz CW信号频率范围的直流。这可以使用六阶切比雪夫滤波器实现,甚至使用用于显示出色带内平坦度的六阶巴特沃兹低通滤波器实现。滤波器阶将被最小化,以限制模拟级的数量和问题点,例如噪声和失真。
结论
在标准评估板上实施的初级和开箱即用测试显示,用于传统正弦波CW生成的基于处理器的DDS技术要实现高性能指日可待。通过精心设计重构滤波器和模拟输出缓冲级,可以实现-120 dBc谐波失真系数。基于DSP的NCO/DDS不只受到单信号音正弦波生成限制。通过使用具备合适的截止频率,且无其他硬件变更的优化AAF(贝塞尔或巴特沃兹),同样的DSP和DAC组合可用作高性能AWG来生成任何类型的波形,例如,完全合成可设置参数的多信号音正弦波(可以完全控制每个分量的相位和幅度)来实施IMD测试。
由于浮点算法对于要求高精度和/或高动态范围的应用至关重要,如今,低成本ADSP-21571 或SoCADSP-SC571 (ARM和SHARC)等SHARC+ DSP处理器实际上是业界的实时处理标准,支持最高10 MSPS的合计采样速率。双SHARC内核和其硬件加速度计采用500 MHz时钟频率,可以提供高于5 Gflops的计算性能和数十个内部专用SRAM,后者是生成各种波形,以及实施复杂的分析处理需要的基本组成部分。此类应用表明,在实施精准的数字信号处理时,并非一定要系统性地使用硬件可编程解决方案。得益于ADI公司的CCES、VDSP++ C和C++编译器,以及全套仿真器和实时调试器,浮点处理器及其整个开发环境可以快速轻松地从仿真器(例如MATLAB)移植代码,以及快速实施调试。
参考文献
1 Joseph A. Webb。美国专利US3654450,1970年4月。
2 Joseph Tierney、Charles M. Rader、Bernard Gold。“数字频率 合成器。”IEEE 音频和电声学论文集,第19卷第1期,1971年3月。
3 Jim Williams、Guy Hoover。AN-132:用于验证纯度的A→D 转换器保真度测试。ADI公司,2011年2月。
4 John F. Hart。计算机逼近算法。Krieger出版公司,1978年。
5 William J. Cody、William Waite。初等函数 软件手册。Prentice-Hall, Inc.,1980年。
6 Robin Green。“更快的数学函数,第2部分介绍。”Sony Computer Entertainment America,2016年5月。
7 Henry T. Nicholas、Henry Samueli。“存在相位累加器截断时的直接数字频率合成器的输出频谱分析。”IEEE,1987年5月。
8 Robert Adams、Khiem Nguyen、Karl Sweetland。“支持分段噪声扰码的113 dB SNR过采样DAC。”IEEE,1998年2月。
ADSP-21000系列应用手册,第1卷。ADI公司,1994年5月。
数字信号合成技术教程。ADI公司,2001年3月。
Butler, Oscar。“2017年夏季实习报告:高精度过采样20位超低功率采集系统。”(ADI公司,2017年)
Crawford, James A. Advanced Phase-Lock Applications: Frequency Synthesis. AMI, LLC, May 2011.
Crawford, James A。高级锁相应用:频率合成。AMI, LLC,2011年5月。
评估板用户指南UG-048。ADI公司,2010年2月。
Goldberg, Bar-Giora。频率合成数字技术。McGraw-Hill,1995年8月。
Ds360型超低失真函数发生器。Stanford Research Systems,1999年。
Symons, Pete。数字波形生成。剑桥大学出版社,2013年11月。
AD1862数据手册。ADI公司,2011年7月。
1241-2010 - 模数转换器术语和测试方法的IEEE标准。IEEE,2011年1月。
作者简介
Patrick Butler是ADI公司南欧销售集团的一名现场应用工程师,为法国全球市场和部分ADEF客户提供支持。从1984年至今,他一直在ADI公司工作,主要负责DSP构建模块IC以及高速转换器的开发。在此以前,他在法国圣艾蒂安斯伦贝谢公司ATE部门工作了5年,任设计工程师,之后法国南特Matra-MHS、AMD和Harris SC-Intersil担任多个应用工程师和FAE职位。如今,他的主要爱好是收集老式音响组件,在两个儿子的帮助下,动手制作高效的有源喇叭扬声器系统。

