教学:基于CPAC的两轴运动控制系统设计与实现
2022-08-28
来源:21ic中国电子网
[导读]摘要:结合计算机可编程自动化控制器(CPAC)平台集成的P2P运动控制模式和DDA插补算法,运用otostudio软件设计相应的两轴运动控制程序和HMI界面,经过调试,程序运行良好,定位准确,实现了CPAC平台对两轴伺服系统运动轨迹的精确控制。
引言
随着科学技术的发展,以液压控制电动化的运动控制为代表的制造业,正经历着深刻的创新和改革。随着电力电子技术的进步,出现了多种多样的控制技术,研究运动控制技术的应用具有十分重要的实用价值。
CPAC平台可以运行windows操作系统,在实现高性能多轴相互协作运动和高速Point-to-Point运动控制的同时,实现常规工控机的功能。CPAC运动控制平台应用更加广泛,适用于有高速、高精度位置控制要求的场合,如CNC数控机床、激光雕刻机、机器人等设备。
1CPAC控制平台的组成结构
CPAC运动控制系统由运动控制器(GUC)、触摸屏(HMI)、伺服驱动器、伺服电机、步进驱动器、步进电机、I/o模块组、端子接线板组成,其中硬件平台由运动控制器(GUC)、人机HMI界面和远程输入/输出模块[1]组成,其核心控制器为由FPGA和DsP组成的运动控制器(GUC)。支持多种运动模式,如点位模式、Jog模式、电子齿轮模式、Fo11ow模式和PT模式等,带有16路通用数字输入、16路通用数字输出[2]。
CPAC软件平台otostudio是一种组态化、图形化的开发工具,基于IEC61131-3编程标准,支持指令表语言(IL)、功能块图(FBD)、连续功能图(CFC)、梯形图(LD)、结构化文本(sT)、顺序功能图(sFC)六种编程语言,同时集成了HMI编程工具,便于用户设计开发HMI界面。
2运动控制设计
2.l运动控制设计
CPAC控制系统中,P2P模式可以很好地实现点位控制,Jog模式可以控制加、减速度的恒速运动,Gear和Fo11ow模式是在主轴运动的基础上做相对运动,PT模式则是做预订轨迹的周期运动。本文选择具有定位准确、控制简单等特点的P2P模式作为系统的运动模式。
为了达到两轴和多轴的合成轨迹的精度要求,需要在普通运动模式的基础上引入插补算法,实现多轴运动的控制。插补就是根据给定进给速度、给定轮廓线形的要求,在轮廓已知点之间,确定一些中间点的方法,称为插补方法或插补原理[4]。限于文章篇幅,选用数字积分法(DDA)作为本设计的插补控制算法。
2.2数字积分法工作原理
数字积分法是利用数字积分原理建立起来的一种插补方法[5],基本原理是将曲线在各轴的进给量分段收集起来,当某个轴的值累加到一个指定的量时就将这个轴的进给量进给一步。
从几何意义上可知,函数y=f(l)对l的积分结果,是此函数曲线与坐标轴l所包围的面积F,如图1所示,即:
若把自变量区间[a,b]等分成由许多有限的小区间△l(其中△l=li+1-li)组成的区间,求面积F可以转换为求小区间面积之和,即:
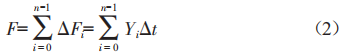
数字运算时,△t一般取单位1,即一个脉冲当量。式(2)可简化为:

当所选取的间隔△t足够小时,可以用求和运算代替积分运算的方法,其误差在允许的误差范围内。
3运动控制的实现
3.1数字积分法的仿真
3.1.1两轴运动直线插补算法及仿真
DDA插补的第一象限两轴直线插补过程简单描述如下:假设一直线的起点为(0,0),终点为(xe,ye),合成轨迹方向的切向速度为,X轴和y轴方向上的速度分量分别是,x和,y,则两方向上对应时间△t的移动位置增量为:

式(4)可整理为:

在△t时间内,x和y的位置增量参数方程为:

动点从起点走向终点的过程,可以看作是经过一个个时间间隔A芒,增量Kλe和KYe累加的结果。经过1次累加后,λ和Y分别都到达终点E(Xe,Ye),下式成立:

令mK=1,则:

由式(10)可知,比例系数K与累加次数m互为倒数。由于m必须是整数,所以K一定是小于1的小数。在选取K时要考虑每次增量Aλ或AY不大于1,以保证坐标轴上进给脉冲不超过一
个进给步长,即:

若假定存储寄存器是n位,则λe和Ye的最大允许寄存容量应为2n-1(各位全1时)。若取K=1则:
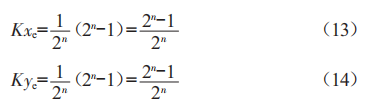
由式(13)(14)可以得出Kλe和KYe小于1。这样,决定了系数K=,就保证了Aλ和AY小于1的条件。因此,轨迹从原点到达结束点的累加次数m就有m==2n次。
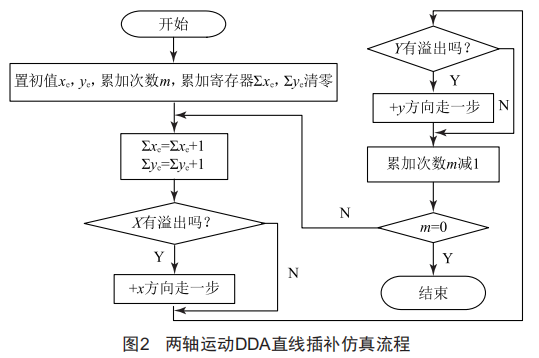
实现两轴运动DDA直线插补时,需要在程序中设定几个存储单元[7],分别用于存放λe和Ye及其累加值Zλe和ZYe。将Zλe和ZYe赋一初始值,在每次插补循环过程中,进行以下求和的
运算过程:

将运算结果的溢出脉冲Aλ和AY用来控制伺服电机转动,两轴运动控制系统合成轨迹即所需的直线轨迹。
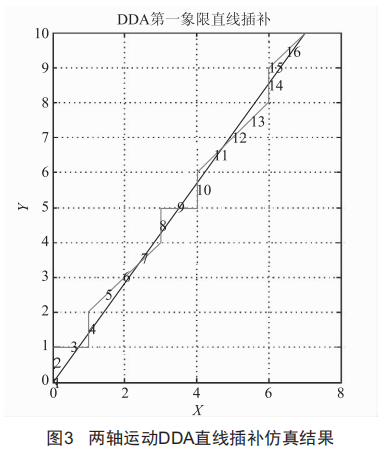
Mat1ab验证两轴运动DDA直线插补仿真流程如图2所示,DDA直线插补结果如图3所示。取程序中累加值的寄存器位数为4位,用Zλe-16来代表溢出。图3中起点坐标为0(0,0),终点坐标为A(7,10),插补步长为1。
3.1.2两轴运动圆弧插补算法及仿真
以第I象限逆圆为例,设两轴合成运动轨迹圆弧运动轨迹为AB,半径为R,运动轨迹的切向速度为⑦,P(λ,Y)为动点,如图4所示,经过整理可得:
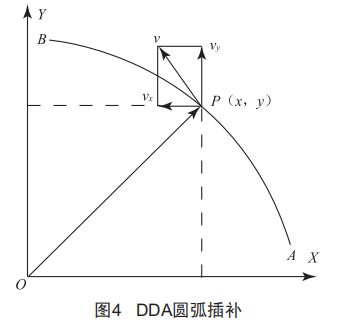
式中,K为比例常数。
由于圆弧运动的半径R为常数,并且切向速度为匀速,所以K可认为是常数。
在单位时间增量A芒内,位移λ和Y增量的参量方程可表示为:

从式(18)(19)可以看出:由于速度分解关系的不同,两轴运动的圆弧插补时的位置增量与两轴运动的直线插补时相比,位移的参量参数发生了变化,λ和Y产生了对调。DDA圆弧插补方法里的位置增量是由当前合成位置坐标(λ,Y)所决定的变量,而直线插补是由终点坐标决定的定值。
对DDA圆弧插补进行Mat1ab仿真,仿真流程如图5所示,仿真结果如图6所示,得到以原点为圆心、半径为5的第一象限的1/4逆圆圆弧。
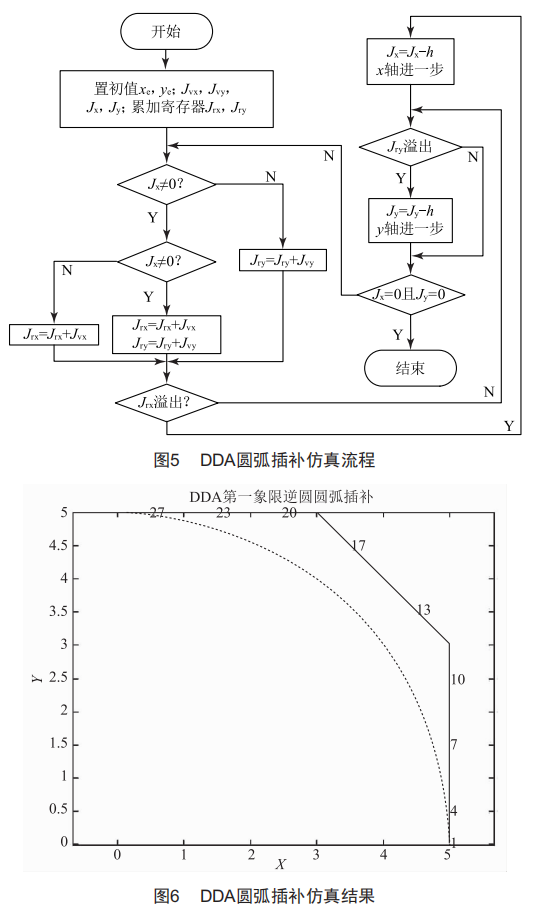
由Mat1ab仿真结果可以看出,直线插补和圆弧插补程序实际运行轨迹和理论运行轨迹始终在一定的范围内贴近,误差不超过一个步长。实际运行轨迹被分成小段,每段内可以分解为x、y轴两个方向的恒定速度的运行。
3.2两轴运动控制程序的设计
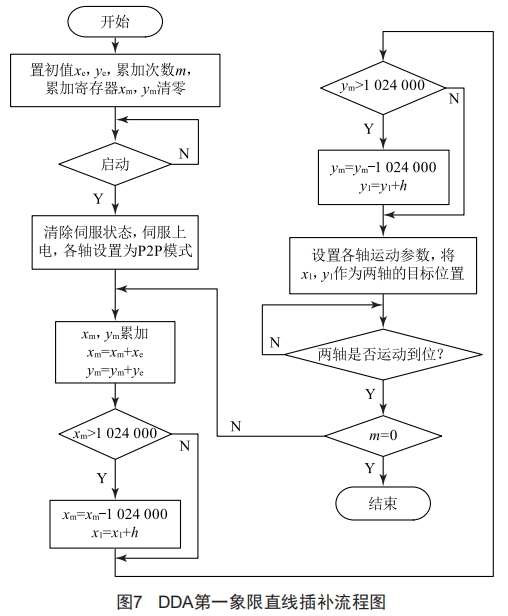
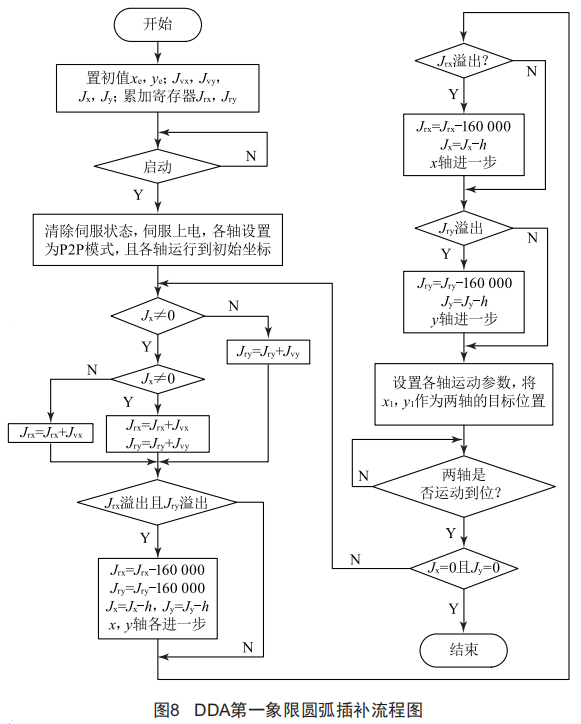
根据上述Mat1ab仿真的插补算法设计的DDA直线插补程序流程图如图7所示,DDA圆弧插补程序流程图如图8所示。
3.3可视界面(HMl)的设计
合理的可视界面设计,能让程序的运行更加高效。
4运行结果与分析
4.1程序的运行结果
经过对otostudio软件的使用,发现在数据监控时,不能监控两轴平面和三轴空间及以上的多维空间位置。下面程序的运行结果采用单轴监控的模式,即一条线代表一个轴的位置状态。
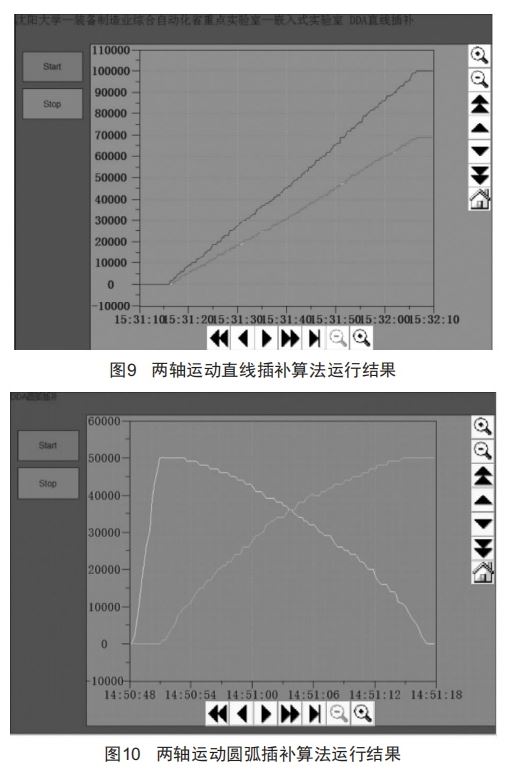
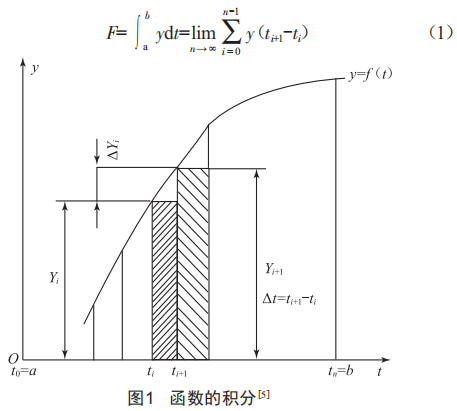
两轴运动直线插补算法运行结果如图9所示,两轴运动圆弧插补算法运行结果如图10所示。
4.2结果分析
从运行结果可以看出,针对不同的坐标,即使程序中设置的各轴运行速度相同,两个轴也是几乎同时到达终点位置。对比DDA直线插补和DDA圆弧插补的Mat1ab仿真实例,可知实际运行轨迹始终在理论运行轨迹附近不超过一个步长的范围内,证明该程序提高了两轴及多轴运动轨迹的控制精度。
5结语
本文基于CPAC运动控制平台来实现对两轴伺服电机的控制,为提高合成运动轨迹的精度,选取了P2P运动模式,引入了两轴直线插补和圆弧插补算法,采用Mat1ab仿真验证了DDA插补算法对于精确运动控制的可行性。在0tostudio软件平台上,实现了P2P运动模式和DDA插补算法控制程序,实现了两轴伺服系统的高精度运动轨迹控制,且程序运行良好,运动轨迹定位准确。
更多信息可以来这里获取==>>电子技术应用-AET<<