流水线设计

　　基本概念

　　流水线处理源自现代工业生产装配线上的流水作业，是指将待处理的任务分解为相对独立的、可以顺序执行的而又相互关联的一个个子任务。流水线处理是高速设计中的一个常用设计手段，如果某个设计的处理流程分为若干步骤，并且整个数据处理是“单流向”的，即没有反馈或者迭代运算，前一个步骤的输出是下一个步骤的输入，那么可以考虑采用流水线设计方法来提高系统频率。流水线设计结构如图所示。

　　其基本结构是将适当划分的n个操作步骤单流向串联起来。流水线操作的最大特点是数据流在各个步骤的处理从时间上看是连续的顺序操作，与此同时各个步骤又是同时并行的在运作。

　　在处理器架构上，一个单核处理器只能一次处理一个任务，是顺序的执行，如要实现并行操作需要多个处理器来执行。

　　FPGA中典型的流水线设计

　　流水线处理采用面积换取速度的思想，可以大大提高电路的工作频率，尤其对于图像处理任务中的二维卷积运算、FIR及FFT滤波器等，采用流水线设计可以保证一个时钟输出一个像素，相对于全并行处理电路占用资源又不会太多。对于大部分的图像处理任务而言，处理过程基本上也是一个“串行”的处理思路。因此，流水线设计无疑是最好的设计方式。如下图所示是一个典型的图像处理任务流程图。

　　并行阵列

　　在并行阵列型电路中，多组并行排列的子电路同时接收整体数据的多个部分进行并行计算。并行阵列型电路中的子电路本身可以是简单的组合电路，也可以是复杂的时序电路例如上面提到的流水线型电路。如果受逻辑资源限制，无法同时处理全部数据，那么也可以依次处理部分数据直到完成全部数据的处理。

　　和流水线共享电路的思路不同，并行阵列电路对于每个处理数据都生成一个处理电路，这无疑更大地提高了电路的处理速度，但是也带来了更大的资源消耗，是用面积换取速度原则的又一体现。如果系统设计对资源消耗相对不敏感，但是又需要较快的处理速度时，那么我们会选择并行结构来完成。

　　并行阵列的一个典型应用是多通道像素同时进行处理，对一个串行输入的RGB通道或是YCbCr通道的视频流，首先做一个串并转换，接着复制处理逻辑对三个通道同时做处理。这样理论上可以得到3倍的速度提升。

　　计算技术

　　计算技术也是图像处理的核心技术之一。在软件算法设计和调试完成之后，需要将软件的算法映射到FPGA中去，由于软件和硬件的设计差异性，相当一部分算法在映射前需要通过等效转换，近似计算等硬件计算技术来转换成硬件易于实现的方式，从而达到逻辑资源消耗和时序，以及误差与消耗的平衡。本节将介绍几种常用的硬件计算技术。

　　算法转换

　　在乘法和除法运算中，经常会遇到乘数、被乘数或分子与分母是常数的情况。直接调用乘法器或除法器当然可以解决这个问题，但是这会消耗一定的DSP运算单元，而DSP单元往往是FPGA里面比较少的资源。对于定常数，可以通过一定的转换将其转换为移位和加法运算，从而减少乘法器和除法器的使用。下面列举几个常用的例子。

　　乘法运算的实现：

　　dout =  din × 255

　　转换后：

　　dout =  din ×（256-1）=（din《8）-din

　　除法运算的实现：

　　在这里扩展了10bit的位宽，这个位宽约大，精度约高，但也会消耗相对更多的资源，实际应用中根据精度需求进行选择。

　　近似计算

　　与算法转换不同的是，算法转换是不会带来任何原理的误差，而近似则会带来一定的计算误差。通常情况下，在误差允许的范围内，采用近似计算带来的明显优势是计算复杂度的降低及资源消耗的降低。在FPGA中常见的近似计算是截断。

　　截断就是用位数较少的近似值来代替位数较多或无限位数的数时，要有一定的取舍法则。在数值计算中，为了适应各种不同的情况，须采用不同的截取方法。

　　经常使用的截断方法就是四舍五入。实际上，对于FPGA来讲，处理的都是二进制数据。因此，在小数位的第一位的值是0还是1决定了是否对结果进行进位。

　　同样，以除法的例子为例：

　　将位宽扩展10bit后，再进行近似运算，近似运算直接去掉了小数部分，引入的误差仅为0.04/210。如果din是图像中的一个像素，其最大值为256，误差仅为0.01，该近似运算几乎不影响图像像素。相对无损失的运算转换，大大减轻了运算量。

　　增量更新

　　增量更新是指在进行更新操作时，只更新需要改变的地方，不需要更新或者已经更新过的地方则不会重复更新，增量更新与完全更新相对。增量更新在流水线处理中，特别是二维卷积处理中特别有用。这是由于在两个连续的卷积窗口中有大量的相同元素。

　　假定要计算连续5个数据流的和，在上一个时刻，这5个待计算的数值是a0,a1,a2,a3,a4,  在本时刻待计算的数值是a1,a2,a3,a4,a5。中间有4个值是相同元素。如此如果每次计算都将5个数重新相加，就有点浪费资源。正确的做法是加上一个新值，再减去一个最老的值。

　　对应的增量计算方法如下图所示，当然5个数值求和，可以扩展到10个数值求和，但增量运算的运算量不变：

　　浮点计算

　　大部分运算可以通过扩位和近似的方式转换为定点运算。但有些算法在设计在设计的过程中就涉及大量的浮点运算，在转换为定点运算时比较麻烦，会带来庞大的工作量。此外，在某些应用中，定点算法是不可行的，动态范围要求使用浮点算法的一个常见的例子是矩阵求逆运算。本节将介绍如何使用FPGA来实现浮点运算以便减少移植的工作量。

　　浮点数的定义

　　浮点数（float）是属于有理数中某特定子集的数的数字表示，在计算机中用以近似表示任意某个实数。具体来说，这个实数由一个整数或定点数（即尾数）乘以某个基数（计算机中通常是2）的整数次幂得到，这种表示方法类似于基数为10的科学记数法。

　　IEEE二进制浮点数算术标准（IEEE 754）是20世纪80年代以来最广泛使用的浮点数运算标准，为许多CPU与浮点运算器所采用。这个标准定义了表示浮点数的格式（包括负零-0）与反常值（denormal number）），一些特殊数值（无穷（Inf）与非数值（NaN）），以及这些数值的“浮点数运算符”；它也指明了四种数值舍入规则和五种例外状况（包括例外发生的时机与处理方式）。

　　IEEE 754规定了四种表示浮点数值的方式：单精确度（32位）、双精确度（64位）、延伸单精确度（43比特以上，很少使用）与延伸双精确度（79比特以上，通常以80位实现）。只有32位模式有强制要求，其他都是选择性的。大部分编程语言都有提供IEEE浮点数格式与算术，但有些将其列为非必需的。例如，IEEE 754在问世之前就有的C语言，现在有包括IEEE算术，但不算作强制要求（C语言的float通常是指IEEE单精确度，而double是指双精确度）。

　　1）单精度浮点数

　　单精度浮点数用32位二进制表示，其中最高位Bit[31],MSB为符号位，即sign域。Bit[30：23]为exponent域，这8位数据表示指数；最低的23位Bit[22：0]为fracTIon域，用于表示浮点数的小数部分。

　　2）双精度浮点数

　　单精度浮点数用64位二进制表示，其中最高位Bit[63],MSB为符号位，即sign域。Bit[62：52]为exponent域，这11位数据表示指数；最低的52位Bit[51：0]为fracTIon域，用于表示浮点数的小数部分

　　用FPGA实现浮点运算

　　乘法：对于乘法运算、位数相乘及指数相加，若位数结果大于2，则需要重新规范化，将其右移一位并且增加指数。由于乘积的位数可能会比表示位多，因此，需要进行舍位处理。两个指数的和包括两个偏移量，因此必须减掉一个。输出值的符号位是输入符号位的异或。需要附加的逻辑来检测下溢出、上移除及处理其他的错误情况，例如，处理无穷大和非数。

　　除法：除法与惩罚类似，只是尾数相除，指数相减并且在重新规范化时可能包含左移。

　　加法和减法：实现要更加复杂。与原码表示相同，实际操作的执行取决于输入的符号。指数必须相同，因为数必须要对齐。根据指数位的差值，将较小的指数右移相应的位数。

　　浮点操作相对于定点操作无疑要消耗更多的资源，这不是因为浮点操作有多复杂，而是因为处理异常时需要很多逻辑，尤其是在需要符合IEEE标准时。大部分FPGA在进行浮点运算时，为符合IEEE 754标准，每次运算都需要去归一化和归一化步骤，导致了极大的性能瓶颈。因为这些归一化和去归一化步骤一般通过FPGA中的大规模桶形移位寄存器实现，需要大量的逻辑和布线资源。通常一个单精度浮点加法器需要500个查找表（LUT），单精度浮点要占用30%的LUT，指数和自然对数等更复杂的数学函数需要大约1000个LUT。因此，随着DSP算法越来越复杂，FPGA性能会明显劣化，对占用80%～90%逻辑资源的FPGA会造成严重的布线拥塞，阻碍FPGA的快速互连，最终会影响时序收敛。

　　存储器映射

　　一般情况下，我们希望当数据流过FPGA时，FPGA尽可能多地处理数据，并且减少FPGA和外部设备之间的数据传输，采用流水线处理架构则可以很好地减少对存储器的频繁读写。然而在某些情况下，一个图像处理算法需要像素之间的行列同步或是帧同步，这个时候就必须要缓存部分图像或者是整幅图像。

　　在软件处理中，这个缓存通常情况下是放在内存中，需要的时候从内存进行读取。在FPGA中，可以选择将缓存放在FPGA内部或者外部。

　　帧缓存

　　对于帧缓存，通常情况下会将其放在片外进行读写。对于帧缓存，在成本不够敏感的情况下，最好使用静态存储器（SRAM），尤其是用于需要频繁和随机地访问这些帧缓存的地方。

　　静态存储器：相对于动态存储器来说，通常情况下读写接口时序相对简单，读写速度要快，并且功耗相对较低。但是，由于静态存储器每一位要使用6个晶体管，而动态存储器每位只使用一个晶体管，因此静态存储器的价格要贵得多。这也限制了它在成本敏感场合的应用。

　　一个帧缓存控制电路要包括读地址发生器、写地址发生器及读写控制时序。一般情况下，这个写地址即为输入帧数据流ImageDin的行列地址，而读地址为输出流Frame_buffer的行列地址。以SRAM为基础的帧缓存电路如图所示。

　　动态存储器：如果系统对于读取速度没有严格要求的缓存应用，那么动态存储器无疑是更好的选择。虽然动态存储器存取速度较慢，从主机提供地址到数据输出可能需要若干个时钟，但是当动态存储器工作在突发模式时，也可以提供较大的带宽，这对于图像处理这样的大数据应用场合非常有用。

　　动态存储器的接口设计相对比较复杂，这是由于动态存储器必须要间隔一段时间对其进行刷新来保持当前的存储器内容。此外，与静态存储器不同，动态存储器的行列地址通常是分开的。因此对动态存储器的寻址工作需要分别进行行列寻址工作。通常情况下，我们会直接采用FPGA厂家提供的IP核来实现外部的存储器驱动，这样可以大大提高开发的效率。

　　行缓存

　　行缓存通常情况下会放在片内。每一个行缓存有效地将输入延迟了一行。用阶数为图像宽度的移位寄存器是可以方便地实现这种延迟。

　　移位寄存器：首先，移位寄存器是由一连串的移位寄存器来实现的，每个位都适用一个寄存器，而每个逻辑单元都只有一个寄存器，因此，采用移位寄存器的方式将会占用大量的逻辑资源，特别是在图像宽度比较大的时候，用内部资源来实现行缓存往往是不明智的选择。

　　片上RAM：设计行缓存时，通常会选择利用FPGA片内的RAM块来实现。采用RAM作为行缓存，就需要设计写入和读出地址产生电路。写入地址就是输入图像行的列地址，读出地址就是输出图像行的列地址。若采用FIFO作为行缓存，则顺序写入与读出即可。

　　行缓存的理想工作状态：流状态是行缓存的理想工作状态，也就是除了缓存装载和卸载，缓存内部的数据流入和流出是平衡的，这样才不至于破坏系统的流水线。输入图像数据的到来时刻是由上一级时序所控制，输出图像的数据流则与行缓存息息相关。

　　考虑一个3×3的窗口滤波器——每个输出结果是窗口内九个像素值的一个函数。如果没有高速缓存，每个窗口位置必须读九个像素（对流处理来说是每个时钟周期），并且当窗口扫描整个图像时，每个像素需要读取九次。在连续的时钟周期内需要使用水平相邻的像素，因此可以用寄存器缓存和延迟像素。这就能将每个时钟周期读取的像素数量减少到三个。行缓冲缓存了之前行中的像素值，避免了对这些行中像素的再次读取。一个3×3的滤波器占据了三行：一个当前行和两个之前行，在当前行中读取新数据，因此需要两个行缓冲来缓存之前两行的像素值。

　　异步缓存

　　异步缓存主要应用在跨时钟的场合。对于一些设计，在不同的部分使用不同的时钟是不可避免的。这个问题主要出现在视频输入、视频输出及与外部的异步接口等场合。

　　一般来说，外部的视频输入数据流都会附带一个视频流的参考时钟，而这个时钟与本地逻辑时钟是异步的。同时，处理完的视频流要进行显示，显示驱动电路的时钟与本地系统时钟往往也是不同的。系统与外部的一些异步接口，例如异步存储器等，都是跨时钟域的场合。

　　异步时钟带来的一个问题就是有效的读写速率不一致。一般情况下，这种场合是读取速度要小于写入速度。解决异步时钟的一个方法就是建立异步缓存器，用一个异步FIFO即可实现。使用FIFO需要注意的问题就是溢出问题，需要使FIFO的读写匹配，在FIFO装满之前，需要把FIFO读走。

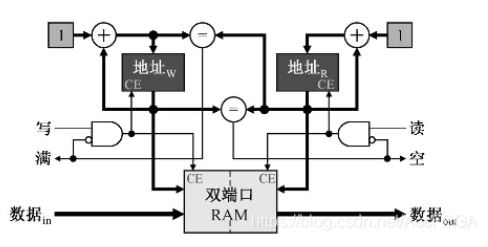
　　FIFO的读写时序比较简单，内部结构图如图所示。

　　对于异步时钟域，用异步FIFO作异步缓存，还能有效解决压稳态的问题。尤其是对于不同频不同相位的异步时钟域，只能用异步缓存来进行同步，这是由于需要缓存来进行带宽匹配，在这里FIFO是一个不错的选择。

　　亚稳态问题：

　　亚稳态状态下，对于任何噪声诸如环境，只要系统中有异步元件，亚稳态就是无法避免的。亚稳态主要发生在异步信号检测、跨时钟域信号传输及复位电路等常用设计中。对于压稳态，一般的处理方法是三拍处理，使用三级寄存器同步后，亚稳态出现的给概率基本为0。

　　在一些对系统稳定性要求更高的场合（例如军工领域），可能还会要求更多拍处理，以便进一步提高系统稳定性。但这种同步方式仅仅适用于同频的异步时钟域或对于少量错误不敏感的功能单元。对于异步时钟域根可靠的方式还是使用两组异步时钟来进行异步缓存。

　更多信息可以来这里获取==>>电子技术应用-AET<<