目前，通用微处理器大多是以字为单位进行操作的，它的指令结构ISA（Instruction-set Architecture）不支持小于一个字的数据操作。而单比特的置换操作在分组密码算法中使用频率非常高，是提高算法安全性的重要手段；而且比特置换操作在处理器中快速高效的特点，也将影响密码处理的整体性能。但在现有的指令结构处理器中，任意的比特置换通常都采用逻辑操作或查找表的方式实现^[1]，即使一个简单的置换操作(如循环移位)，也需要多条指令才能完成。根据相关研究可知，一个n比特的置换操作，它的指令级复杂度是O(n)，处理速度也将随着n的增大而不断降低。对于目前实时的网络通信来说，这显然是不可容忍的。因此，针对这一问题在一些专用指令集微处理器ASIP(Application-Specific Instruction-Set Processor)中，增加了特殊的置换指令，如多媒体处理器PLX中增加了MIX、MUX和Perm等指令^[2]，但这些指令并不能满足n-bit数据的任意置换操作。本文提出了一种在处理器中实现比特置换的方法，给出了相应的比特置换指令及其操作结构。
1 密码学中的比特置换及其一般实现方式
1.1 密码学中的比特置换
　　比较置换操作能使输入数据中第i比特置换到输出数据的第j比特上，而且置换过程中各位源数据之间不发生计算关系。输入的n比特数据需要log2n比特位置信息或配置信息。
　　置换是密码算法中隐藏明文信息中冗余度的重要手段，通过位置置换可以实现明文到密文的扩散。置换按明密文映射关系分为三类：直接置换、扩展置换和压缩置换。直接置换指明密文间是一一映射关系，且明文的每一位都有到密文的映射；扩展置换指明密文间为一对多的映射关系，它使得密文对明文的依赖性传播得更快；压缩置换指明密文间是一一映射关系，但并不是明文的每一位都有到密文的映射。置换输入和输出位宽根据算法和置换类型的不同而有所不同。例如DES算法中有64-bit初始置换IP、末尾置换IP-1以及轮运算中的32-bit P置换^[3]。
1.2 逻辑操作方式
　　逻辑操作方式是指采用AND、OR、SHIFT等简单逻辑操作实现复杂的比特置换操作。在此方式下，每对1 bit进行置换，处理器需要进行四步操作：①产生目标比特的MASK参数；②提取相应比特值(AND指令)；③将该比特移至相应位置(SHIFT指令)；④存储到相应寄存器中(OR指令)。由上述过程可知，一个n-bit的置换操作需要4n条指令才能完成。尽管一些处理器中针对这一问题有所改进，将1 bit置换操作的指令压缩到2条——汲取指令(EXTRACT)和放置指令(DEPOSIT)，但n-bit置换操作仍需要2n条指令，处理性能没有明显提高。
1.3 查找表方式
　　查找表方式是另一种实现比特置换的方法，它在速度上与逻辑操作相比有所提高，但需要大量的存储空间放置控制信息。完成一个n-bit的置换操作需要m个查找表，每个表的容量为2n/m×nbit。以64-bit输入数据为例，当m=1时，完成一次任意置换需要一个264×64bit的查找表，这在现有微处理器结构中是无法实现的；当m=8时，完成一次任意置换需要8个容量为28×64bit的查找表。每个表代表源操作数中连续8-bit的置换，表中除了8-bit置换的目标位置外，其他位置均为0，此时共需要23条指令来完成64-bit置换：8条Extract指令获得表的索引值、8条Load指令置换相应比特、7条OR指令链接8个8-bit置换后的数据。这种方法相对于逻辑操作方式来说指令条数减少了很多，但它在实际执行中，Load指令往往遇到未命中Cache的情况，所以实现n-bit的置换操作需要的复杂度一般为O(n)。
2 比特置换操作的优化实现
2.1 Butterfly结构
　　目前，Butterfly结构^[4]及其他一些相似的结构都广泛应用于信息处理领域中，如数字信号处理中的快速傅里叶变换(FFT)等。图1(a)中给出了8-bit输入的Butterfly结构，图1(b)中给出了相应的Inverse Butterfly结构。

2.2 Benes网络结构
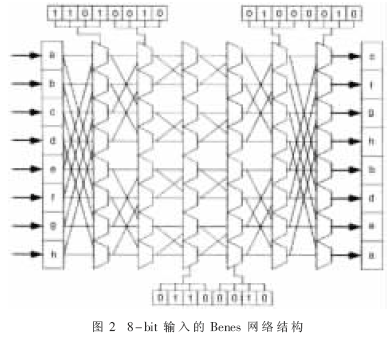
　　Benes网络结构由一个Butterfly结构链接一个Inverse Butterfly结构组成，它是一种可重排网络，能实现输入端到输出端的所有置换。完成n-bit置换操作需log2n级Butterfly变换和log2n级Inverse Butterfly变换。对于一个64-bit置换，则需要2log2n=12级变换，且每一级需要n/2-bit配置信息。在处理器中执行置换操作需要一条Butterfly指令和一条Inverse Butterfly指令及log2n个n-bit配置信息。
　　图2给出了一个8-bit输入的Benes网络结构，能完成(abcdefgh)到(cfghbdea)的置换。根据配置信息，它的置换过程如下：Butterfly指令完成(abcdefgh)->(abgdefch)->(gdabehcf)->(dgabehfc)；Inverse Butterfly指令完成(dgabehfc)->(gcbaehcf)->(bdgacfeh)->(cfghbdea)。

2.3 比特置换指令
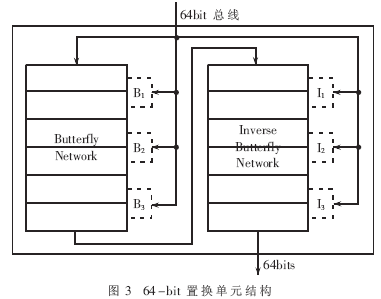
　　比特置换单元内部设置了一定的缓存区，用于存储配置信息，如图３所示的B1、B2、B3和I1、I2、I3。由于不同ASIP中指令格式存在差异，这些内部缓存区是可选择的。由于Inverse Butterfly指令类似于Butterfly指令，下面以Butterfly指令为例进行说明。对于超长指令字格式(VLIW)，支持多操作数方式，不需要内部寄存器存储配置信息，其指令可描述为：Butterfly Rd，Rs，B1，B2，B3。其中Rd为置换数据目的地址，Rs为置换数据源地址，B1、B2、B3为配置信息的外部存储地址，即一条Butterfly指令包括Rs、B1、B2、B3四个源操作数。对于精简指令格式(RISC)，最多支持两个源操作，相应指令可描述为：Butterfly Rd，Rs，B3。即需要将配置信息B1、B2、I1、I2在进行置换操作前装入到置换单元内部缓存区中，而B3、I3则从外部存储器中获得。对于超标量结构处理器，假设其有两路并行处理通路，则Butterfly指令与Inverse Butterfly指令可并行执行。对于所采用的不同指令格式，具体操作指令数也不同。

3 性能比较
　　如果一个处理器可以支持比特置换操作，则其比特置换操作的延时必须与逻辑运算单元(ALU)的时钟频率相匹配。在ALU中主要是乘法器^[5]延时较大，通常占用3~5个时钟周期" title="时钟周期">时钟周期，因此只有使比特置换操作延时小于乘法运算延时，才能在不影响处理器整体性能的前提下，使处理器支持比特置换操作。而逻辑操作方式与查找表方式的比特置换实现方法所占用的时钟周期都远远大于3个时钟周期，如表1所示。当采用Benes网络结构时，仅执行两次Butterfly指令，在性能上得到了很大提高，使n-bit 的比特置换操作的复杂度从O(n)降至O(log(n))。