随着信息时代的到来，数字信号处理已经成为当今一门极其重要的学科和技术，并且在通信、语音、图像、自动控制等众多领域得到了广泛的应用。在数字信号处理中，数字滤波器" title="数字滤波器">数字滤波器占有极其重要的地位，它具有精度高、可靠性好、灵活性大等特点。现代数字滤波器可以用软件或硬件两种方式来实现。软件方式实现的优点是可以通过滤波器参数的改变去调整滤波器的性能。
　　MATLAB是一种面向科学和工程计算的语言，它集数值分析、矩阵运算、信号处理和图形显示于一体，具有编程效率高、调试手段丰富、扩充能力强等特点。MATLAB的信号处理工具箱具有强大的函数功能，它不仅可以用来设计数字滤波器，还可以使设计达到最忧化，是数字滤波器设计的强有力工具。
1 FIR滤波器的设计
1.1 FIR滤波器简介^[1]
　　根据冲激响应的时域特性，数字滤波器可分为无限长冲激响应滤波器（IIR）和有限长冲激响应滤波器（FIR）。FIR的突出优点是：系统总是稳定的、易于实现线性相位、允许设计多通带（或多阻带）滤波器，但与IIR相比，在满足同样阻带衰减的情况下需要的阶数较高。滤波器的阶数越高，占用的运算时间越多，因此在满足指标要求的情况下应尽量减少滤波器的阶数。
　　FIR滤波器的基本结构可以理解为一个分节的延时线，把每一节的输出加权累加，可得到滤波器的输出。FIR滤波器的冲激响应h(n)是有限长的，数学上M阶FIR滤波器可以表示为：
　　
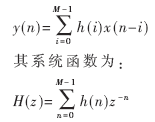
　　FIR滤波器的设计问题实质上是确定能满足所要求的转移序列或脉冲响应" title="脉冲响应">脉冲响应的常数的问题，设计方法主要有窗函数法、频率采样法和等波纹最佳逼近法等。
1.2 窗函数设计法的步骤^[3][4]
　　窗函数设计法是一种通过截短和计权的方法使无限长非因果序列成为有限长脉冲响应序列的设计方法。通常在设计滤波器之前，应该先根据具体的工程应用确定滤波器的技术指标。在大多数实际应用中，数字滤波器常常被用来实现选频操作，所以指标的形式一般为在频域中以分贝值给出的相对幅度响应和相位响应。
　　用窗函数法设计FIR滤波器的步骤如下：
　　（1）根据过渡带宽及阻带衰减要求，选择窗函数的类型并估计窗口长度N（或阶数M=N-1）。窗函数类型可根据最小阻带衰减AS独立选择，因为窗口长度N对最小阻带衰减A_S没有影响。在确定窗函数类型以后，可根据过渡带宽小于给定指标确定所拟用的窗函数的窗口长度N。设待求滤波器的过渡带宽为△ω，它与窗口长度N近似成反比。窗函数类型确定后，其计算公式也确定了，不过这些公式是近似的，得出的窗口长度还要在计算中逐步修正。原则是在保证阻带衰减满足要求的情况下，尽量选择较小的N。在N和窗函数类型确定后，即可调用MATLAB中的窗函数求出" title="求出">求出窗函数w_d(n)。
　　（2）根据待求滤波器的理想频率响应求出理想单位脉冲响应hd(n)。如果给出待求滤波器的频率响应为H_d(e^jω)，则理想的单位脉冲响应可以用下面的傅里叶反变换式求出：
　　
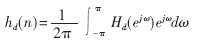
　　在一般情况下，h_d(n)是不能用封闭公式表示的，需要采用数值方法表示。从ω=0到ω=2π采样N点，采用离散傅里叶反变换(IDFT)即可求出。
　　（3）计算滤波器的单位脉冲响应h(n)。它是理想单位脉冲响应和窗函数的乘积，即h(n)=h_d(n)·w_d(n)，在MATLAB中用点乘命令表示为h=hd·wd。
　　（4）验算技术指标是否满足要求。为了计算数字滤波器在频域中的特性，可调用freqz子程序，如果不满足要求，可根据具体情况，调整窗函数类型或长度，直到满足要求为止。
　　使用窗函数法设计时要满足以下两个条件：
　　（1）窗谱主瓣尽可能地窄，以获得较陡的过渡带；
　　（2）尽量减少窗谱的最大旁瓣的相对幅度，也就是使能量尽量集中于主瓣，减小峰肩和纹波，进而增加阻带的衰减。
　　根据工程经验，给定的滤波器指标参数一般为通带截止频率" title="截止频率">截止频率ω_p、阻带截止频率ω_s、实际通带波动R_p和最小阻带衰减A_s。窗函数设计的经验公式为：
　　
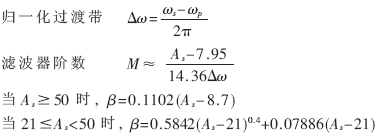
　　在实际工程中常用的窗函数有五种，即矩形窗、三角窗、汉宁窗、海明窗和凯泽窗。这些窗函数在MATLAB中分别用boxcar、triang、hanning、hamming、kaiser实现，它们之间的性能比较如表1所示。

2 MATLAB环境下的设计实例^[2][4]
2．1 高通滤波器的设计
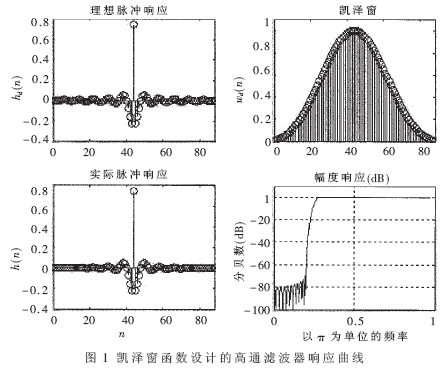
　　用窗函数设计高通滤波器，性能指标如下：通带截止频率ω_s=0.2π，阻带截止频率ω_p=0.3π，实际通带波动R_p=0.25dB,最小阻带衰减A_s=70dB。
　　分析：从表1可以看出凯泽窗能提供74dB的最小阻带衰减，所以选用凯泽窗进行设计，程序主要部分如下：
　　As=70;
　　ωs=0.2*π;
　　ωp=0.3*π
　　tr_width=ωp-ωs;　　　　　　　　　　　　　　　　%计算过渡带宽
　　M=ceil((As-7.95)*2*π/(14.36*tr_width)+1)+1;　　　 %按凯泽窗计算滤波器长度
　　disp([’滤波器的长度为’,num2str(M)]);
　　beta=0.1102*(As-8.7); %计算凯泽窗的β值
　　n=[0:1:M-1];
　　disp([’线性相位斜率为’,num2str(beta)]);
　　　　w_kai=(kaiser(M,beta))’; %求凯泽窗函数
　　　　ωc=(ωs+ωp)/2;
　　　　hd=ideal_lp(π,M)-ideal_lp(ωc,M); %求理想脉冲响应
　　　　h=hd.*w_kai; %设计的脉冲响应为理想脉冲响应与窗函数乘积
　　　　[db,mag,pha,grd,ω]=freqz_m(h,^[1]);
　　　　delta_ω=2*π/1000;
　　　　Rp=-(min(db(ωp/delta_ω+1:1:501)));
　　　　disp([’实际通带波动为’,num2str(Rp)]);　　　%以下为作图程序
　　　　As=-round(max(db(1:1:ωs/delta_ω+1)));
　　　　disp([’最小阻带衰减为’,num2str(As)]);
　　　　　　subplot(1,1,1);
　　　　　　subplot(2,2,1);
　　　　　　stem(n,hd);
　　　　　　title(’理想脉冲响应’);　
　　　　　　axis([0 M-1 -0.4 0.8]);
　　　　　　ylabel(’hd(n)’);
　　　　　　subplot(2,2,2);
　　　　　　stem(n,w_kai);
　　　　　　title(’凯泽窗’);
　　　　　　 axis([0 M-1 0 1.1]);
　　　　　　ylabel(’wd(n)’);
　　　　　　subplot(2,2,3);
　　　　　　stem(n,h);
　　　　　　title(’实际脉冲响应’);
　　　　　　axis([0 M-1 -0.4 0.8]);
　　　　　　xlabel(’n’);ylabel(’h(n)’);
　　　　　　subplot(2,2,4);
　　　　　　plot(ω/π,db);
　　　　　　title(’幅度响应/dB’);
　　　　　　axis([0 1 -100 10]);
　　　　　　grid;
　　　　　　xlabel(’以π为单位的频率’);
　　　　　　ylabel(’分贝数/dB’);
　　程序运行结果如图1所示。实际通带波动为0.04369,最小阻带衰减为70，滤波器长度为89，线性相位斜率为6.7553,符合设计要求。

2．2 低通滤波器的设计
　　用窗函数设计低通滤波器，性能指标如下：通带截止频率ω_p=0.1π，阻带截止频率ω_s=0.25π，实际通带波动R_p=0.10dB,最小阻带衰减A_s=40dB。
　　分析：从表1可以看出，汉宁窗、海明窗和凯泽窗能提供大于40dB的最小阻带衰减。但汉宁窗的旁瓣峰值较小，而主瓣宽度和海明窗一样。可以使滤波器的阶数较少，所以选用汉宁窗进行设计，程序主要部分如下：
　　ωp=0.10*π;
　　ωs=0.25*π;　
　　tr_width=ωs-ωp; %计算过渡带宽
　　M=ceil(6.6*/tr_width)+1; %按汉宁窗计算滤波器长度
　　disp([’滤波器的长度为’,num2str(M)]);
　　n=0:M-1;
　　ωc=(ωs+ωp)/2; %截止频率取为两边缘频率的平均值
　　hd=ideal_lp(ωc,M); %求理想脉冲响应
　　w_han=(hanning(M))’; %求汉宁窗函数
　　h=hd.*w_han; %设计的脉冲响应为理想脉冲响应与窗函数乘积
　　[db,mag,pha,grd,ω]=freqz_m(h,^[1]);%以下为作图语句
　　delta_ω=2*π/1000;
　　Rp=-(min(db(1:1: ωp/delta_ω+1)));
　　disp([’实际通带波动为’,num2str(Rp)]); %以下为作图程序
　　As=-round(max(db(ωs/delta_ω+1:1:501)));
　　disp([’最小阻带衰减为’,num2str(As)]);
　　　　subplot(221)
　　　　stem(n,hd);
　　　　title(’理想冲击响应’),
　　　　axis([0 M-1 -0.1 0.3]);
　　　　ylabel(’hd(n)’);
　　　　subplot(222)
　　　　stem(n,w_han);
　　　　title(’汉宁窗’),
　　　　axis([0 M-1 0 1.1]);
　　　　ylabel(’wd(n)’);
　　　　subplot(223)
　　　　stem(n,h);
　　　　title(’实际冲击响应’),
　　　　axis([0 M-1 -0.1 0.3]);
　　　　xlabel(’n’);
　　　　ylabel(′h(n)′);
　　　　subplot(224);
　　　　plot(ω/π,db);
　　　　title(′幅度响应（db)′);
　　　　axis([0 1 -100 10]),
　　　　grid;
　　　　xlabel(′以π为单位的频率′);
　　　　ylabel(′分贝数′);
　　　　仿真结果如图2所示。实际通带波动为0.076565,最小阻带衰减为44，滤波器长度为67，符合设计要求。